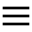A Baker’s Dozen of Problems
This article is a collection of open problems, with brief historical and bibliographical comments, somewhat in the spirit of the problem with which V. Arnold opened his famous seminar every semester and that were recently collected and published in a book form.
1 Commuting Billiard Ball Maps
Given a convex plane domain, the billiard ball map sends the $\def\R{\mathbb{R}}$ incoming ray (the trajectory of the billiard ball) to the outgoing one: the law of reflection is “the angle of incidence equals the angle of reflection”.
Consider two nested convex domains. Then one has two billiard ball maps, $T_{1}$ and $T_{2}$, acting on the oriented lines that intersect both domains. If the domains are bounded by confocal ellipses, then the respective billiard ball maps commute; see, e.g., Tabachnikov [2005] .
Assume that the two maps commute: $T_{1}\circ T_{2}=T_{2}\circ T_{1}$.
Conjecture 1.
The two domains are bounded by confocal ellipses.
For outer (a.k.a. dual) billiards, an analogous fact is proved in Tabachnikov [1994] . For piece-wise analytic billiards, this conjecture was proved by Glutsyuk [2014] .
Of course, this problem has a multi-dimensional version, open both for inner and outer billiards.
2 Can One-Parameter Families of 2- and 3-Periodic Billiard Trajectories Coexist?
A curve of constant width admits a one-parameter family of 2-periodic (back and forth) billiard trajectories. Likewise, for every $p\geq 3$, there exist billiard tables admitting a one-parameter family of $p$-periodic billiard trajectories; see Baryshnikov and Zharnitsky [2006] for a recent approach using ideas of sub-Riemannian geometry.
Problem 1.
Are there smooth convex curves, other than ellipses, simultaneously admitting one-parameter families of $p$- and $q$-periodic billiard trajectories (for $p\neq q$)?
The simplest case of the question is whether any curve of constant width, other than a circle, admits a one-parameter family of 3-periodic billiard trajectories.
A similar question can be asked about outer billiards.
3 Birkhoff’s Theorem for Lorentz Billiards
The classical Birkhoff theorem states that, for every $n\geq 3$ and $1\leq k\leq n/2$, the billiard system inside a plane oval has at least two $n$-periodic trajectories with the rotation number $k$. Consider the billiard system inside an oval in the Lorentz plane with the pseudo-Euclidean metric $ds^{2}=dx^{2}-dy^{2}$. Is there an analog of Birkhoff’s theorem in this set-up?
Billiard trajectories in pseudo-Euclidean space can be of three types: space-like, time-like, and light-like, see Khesin and Tabachnikov [2009] for Lorentz billiards. One would expect separate existence statements for space-like and time-like trajectories .
A convex body in $\R^{n}$ has at least $n$ diameters (2-periodic billiard trajectories). If the ambient space is pseudo-Euclidean, $\R^{p,q}$, then there are at least $p$ space- and at least $q$ time-like diameters ( Khesin and Tabachnikov [2009] ). A lower bound on the number of periodic billiard trajectories in multi-dimensional Euclidean space is obtained in Farber and Tabachnikov [2002] . What happens with multi-dimensional pseudo-Euclidean billiards?
4 Polygonal Outer Billiards in the Hyperbolic Plane
The outer billiard about a convex polygon $P$ in the plane $\R^{2}$ is a piece-wise isometry, $T$, of the exterior of $P$ defined as follows: given a point $x$ outside of $P$, find the support line to $P$ through $x$ having $P$ on the left, and define $T(x)$ to be the reflection of $x$ in the support vertex (Fig. 1 ). See Dogru and Tabachnikov [2005] , Tabachnikov [2005] .
The orbit structure for a regular dodecagon
C. Culter proved that every polygon in the affine plane admits periodic outer billiard orbits, see Tabachnikov [2007] . Outer billiard can be defined on the sphere and in the hyperbolic plane. On the sphere, there exist polygons without periodic outer billiard orbits.
Conjecture 2.
Every polygonal outer billiard in the hyperbolic plane has periodic orbits. These orbits may lie on the circle at infinity.
Note that an analogous question for inner polygonal billiards in the Euclidean plane is a hard problem, open even for triangles. The “world record” here belongs to Schwartz [2009] .
Another problem is to describe polygonal outer billiard tables in the hyperbolic plane for which all orbits are periodic. For example, right-angled regular $n$-gons (with $n\geq 5$) have this property ( Dogru and Tabachnikov [2003] ). In the affine plane, every outer billiard orbit about a lattice polygon is periodic.
5 Periodic Orbits of Multi-Dimensional Outer Billiards
Outer billiards are defined in even-dimensional spaces as well. Let $M\subset\R^{2n}={\mathbb{C}}^{n}$ be a smooth hypersurface. The tangent line at a point $x\in M$ is defined as the line spanned by the vector $J(N_{x})$ where $J$ is the operator of multiplication by $\sqrt{-1}$ and $N_{x}$ is a normal vector to $M$ at $x$. Two points, $y$ and $z$, outside of $M$ are in the outer billiard relation if they lie on a tangent line to $M$ at point $x$ and $|yx|=|zx|$. This relation is symplectic (with respect to the linear symplectic structure in $\R^{2n}$). If $M$ is strictly convex, this correspondence is a symplectic map, see Tabachnikov [1995] .
For every $p\geq 3$, this outer billiard map has $p$-periodic orbits ( Tabachnikov [1995] ). One expects a much stronger lower bound for the number of periodic orbits; for $p=3$, this number is no less than $2n$, the dimension of the ambient space ( Tabachnikov [2003]).
Problem 2.
Find analogous lower bounds for other values of $p$. See Farber and Tabachnikov [2002] for the number of periodic trajectories in multi-dimensional inner billiards.
6 A Converse Desargues Theorem
A classical Desargues theorem states the following. Consider a pencil of conics (a one-parameter family of conics sharing four points—these points may be complex or multiple, as for the family of concentric circles). The intersections of a line $\ell$ with these conics define an involution on $\ell$, and the theorem states that this involution is a projective transformation of $\ell$.
Let $f(x,y)$ be a polynomial with a non-singular value 0. Let $\gamma$ be an oval which is a component of the algebraic curve $f(x,y)=0$. Assume that the curves $\gamma_{\varepsilon}=\{f(x,y)=\varepsilon,\ \varepsilon>0\}$ foliate an outer neighborhood of $\gamma$ and that, for every tangent line $\ell$ to $\gamma$, its intersections with the curves $\gamma_{\varepsilon}$ define a (local) projective involution on $\ell$.
Problem 3.
Prove that $\gamma$ is an ellipse and the curves $\gamma_{\varepsilon}$ form a pencil of conics.
A particular case, in which the involutions under consideration are central symmetries of the line, is proved in Tabachnikov [2008] .
7 Cayley Theorem for Null Geodesics on an Ellipsoid in Minkowski Space
The following Poncelet-style theorem was proved in Genin et al. [2007] . Consider an ellipsoid
| $\frac{x^{2}}{a}+\frac{y^{2}}{b}+\frac{z^{2}}{c}=1,\quad a,b,c>0$ |
in three dimensional Minkowski space with the metric $dx^{2}+dy^{2}-dz^{2}$. The induced metric on the ellipsoid degenerates along the two “tropics”
| $z=\pm c\sqrt{\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}};$ |
the metric is Lorentz, of signature $(+,-)$, in the “equatorial belt” bounded by the tropics. Through every point of the equatorial belt there pass two null geodesics of the Lorentz metric, the “right” and the “left” ones.
Call a chain of alternating left and right null geodesics, going from tropic to tropic, an $(n,r)$-chain if it closes up after $n$ steps and making $r$ turns around the equator. The theorem states that if there exists an $(n,r)$-chain of null geodesics then every chain of null geodesics is an $(n,r)$-chain.
Problem 4.
Find conditions on the numbers $a,b,c$ ensuring the existence of $(n,r)$-chains.
For the classical Poncelet porism, such a formula is due to Cayley, see Griffiths and Harris [1978] , Barth [1996] , Dragovic and Radnovic [2011] , Flatto [2009] .
8 Origami Hyperbolic Paraboloid

There is a well known origami construction depicted in Fig. 2. The pleated surface looks like a hyperbolic paraboloid and is often called so in the origami literature.
The problem is to explain this construction. If one assumes that paper is not stretchable and the fold lines are straight then one can prove that this construction is mathematically impossible, see Demaine et al. [2011]. The explanation offered in Demaine et al. [2011] is that there exist invisible folds along the diagonals of the elementary trapezoids in Fig. 2 left. Assuming this to hold, and given a particular patterns of these diagonals (one can choose one of the two for each trapezoid), what is the shape of the piece-wise linear surface obtained by folding?

A more general question: what is the result of a similar construction for other patterns of folding lines? (see, e.g., Fig. 3). See Fuchs and Tabachnikov [1999] concerning folding paper along curved lines and the books (Demaine et al. [2007], O’Rourke [2011]) for mathematical paper folding.
9 The Unicycle Problem
A mathematical model of a bicycle is an oriented unit segment $AB$ in the plane that can move in such a way that the trajectory of the rear end $A$ is always tangent to the segment, see Foote et al. [2013] . Sometimes the trajectories of the rear and front points $A$ and $B$ coincide (say, riding along a straight line).
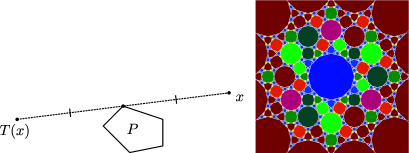
The following construction is due to D. Finn. Let $\gamma(t),t\in[0,L]$ be an arc length parameterized smooth curve in the plane which coincides with all derivatives, for $t=0$ and $t=L$, with the $x$ axis at points $(0,0)$ and $(1,0)$, respectively. One uses $\gamma$ as a “seed” trajectory of the rear wheel of a bicycle. Then the new curve $\Gamma=T(\gamma)=\gamma+\gamma^{\prime}$ is also tangent to the horizontal axis with all derivatives at its end points $(1,0)$ and $(2,0)$. One can iterate this procedure yielding a smooth infinite forward bicycle trajectory ${\cal T}$ such that the tracks of the rear and the front wheels coincide. See Fig. 4, left.
It is proved in Levi and Tabachnikov [2009] that the number of intersections of each next arc of ${\cal T}$ with the $x$ axis is greater than that of the previous one. Likewise, the number of local maxima and minima of the height function increases with each step of the construction. And so does the number of inflection points.
Conjecture 3.
Unless $\gamma$ is a straight segment, the amplitude of the curve ${\cal T}$ is unbounded, i.e., ${\cal T}$ is not contained in any horizontal strip; ${\cal T}$ is not a grap;, and ${\cal T}$ is not embedded, that is, it starts to intersect itself.
Here is a related problem. Given an oriented oval $\gamma$, draw the unit tangent segments to $\gamma$, and let $\gamma_{1}$ be the locus of their endpoints. We get a map $\gamma\mapsto\gamma_{1}$.
Conjecture 4.
If all iterations of this map are convex curves then $\gamma$ is a circles, see Fig. 4, right.
A certain justification is a linearization of this statement, which is a theorem: Let $F$ be a periodic function, and consider the linear map $F\mapsto F+F^{\prime}$. If all iterations of $F$ are positive then $V$ is a positive constant.
10 Self-Dual Curves and Surfaces
Projective duality is a correspondence between points of the real projective plane ${\mathbb{RP}}^{2}$ and lines of the dual projective plane $({\mathbb{RP}}^{2})^{*}$; projective duality extends to smooth and piece-wise smooth curves, taking a curve $\gamma\subset{\mathbb{RP}}^{2}$, a one-parameter family of points, to the envelope $\gamma^{*}\subset({\mathbb{RP}}^{2})^{*}$ of the respective one parameter family of dual lines. A curve $\gamma$ is called projectively self-dual if there exists a projective transformation from ${\mathbb{RP}}^{2}$ to $({\mathbb{RP}}^{2})^{*}$ that takes $\gamma$ to $\gamma^{*}$. Likewise one defines self-dual polygons.
The problem of describing projectively self-dual curves is poorly understood, it is Arnold’s problem 1994–17 ( Arnold [2004] ). In Fuchs and Tabachnikov [2009] , a description of projectively self-dual polygons is given and some results on self-dual curves were obtained.
Problem 5.
Extend the results of Fuchs and Tabachnikov [2009] to projectively self-dual polyhedra, and to projectively self-dual polygons in multi-dimensional projective spaces.
A non-degenerate curve $\gamma$ in ${\mathbb{RP}}^{n}$ has the osculating hyperplane at each point; a hyperplane in ${\mathbb{RP}}^{n}$ is a point in the dual projective space $({\mathbb{RP}}^{n})^{*}$, and this one-parameter family of points in $({\mathbb{RP}}^{n})^{*}$ is the dual curve $\gamma^{*}$.
All these problems have affine analogs, in which the curves (hypersurfaces) are assumed to be star-shaped, and the projective duality is replaced by the polar duality.
11 New Configuration Theorems of Projective Geometry
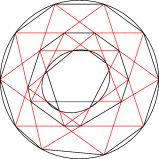
then the inner one is also inscribed into a conic
A number of new configuration theorem of elementary projective geometry were described in Schwartz and Tabachnikov [2010]. Only in some cases geometric proofs are known; the rest is a “brute force” computer computation (and in one case, the computation is too large for computer). The problem is to understand what is going on and to find conceptional proofs and possible generalizations to these theorems.
In particular, the configuration theorem depicted in Fig. 5 is not really a theorem, since one only has numerical evidence for it. Find a proof.
The motivation comes from the recent work on the pentagram map, a discrete completely integrable system acting on projective polygons, see, e.g., Ovsienko et al. [2010].
12 Totally Skew 3-Dimensional Disc in 7-Dimensional Space?
A submanifold $M^{k}\subset\R^{n}$ is called totally skew if, for every two distinct points $x,y\in M$, the tangent spaces at these points are in general position (i.e., their affine span has dimension $2k+1$). Clearly, a necessary condition for being totally skew is $n\geq 2k+1$. It is proved in Ghomi and Tabachnikov [2008] that if $M^{k}$ is a totally skew disc in $\R^{2k+1}$ then $k\in\{1,3,7\}$. For $k=1$, a simple example is given by the cubic curve $(t,t^{2},t^{3}),\ t\in\R$.
Problem 6.
Is there a totally skew 3-disc in $\R^{7}$?
13 Areas and Dissections into Triangles
If a square is dissected into triangles of equal areas then the number of these triangles must be even. This theorem has a surprisingly difficult proof, see Stein and Szabo [1994]. There are many similar results (proved along the same lines), for example, the square can be replaced by any centrally symmetric polygon (Monsky [1990]).
An attempt to understand this result leads to the following question. Consider a partition of a square (of unspecified size) into $n$ triangles. We allow small perturbation of triangles, so that each “free” vertex has two degrees of freedom and each vertex on a side has one degree of freedom. Denote by $M$ the “moduli space” of partitions with the same combinatorics, i.e., obtained from a given one by small perturbations, so that no triangle degenerates.
Claim 1.
The dimension of $M$ equals $n-1$.
(Proof: the sum of all angles in sight is $\pi$ times the number of triangles. A ‘free’ vertex with two degrees of freedom contributes $2\pi$, and a vertex on a side, having one degree of freedom, contributes $\pi$. The four corners contribute $\pi/2$ each, and one has one degree of freedom for scaling.)
Assign to every partition in $M$ the ordered set of areas of its triangles. This gives a map $M^{n-1}\to\R^{n}$; this map is component-wise quadratic (the area of triangle is given by a determinant). It follows that there exists a polynomial relation between the areas $a_{1},\dots,a_{n}$ depending only on the combinatorics of the partition.
Problem 7.
What can be said about this polynomial relation? For example, how to find the least degree of this polynomial in terms of the combinatorics of the partition?
See Abrams and Pommersheim [2014] for the first steps in this direction. See also Kantor and Maydanskiy [2003] for a description of the dissections for which this polynomial is linear.
References
- Abrams and Pommersheim [2014] Abrams, A., Pommersheim, J.: Spaces of polygonal triangulations and Monsky polynomials. Discrete Comput. Geom. 51, 132–160 (2014)
- Arnold [2004] Arnold, V.: Arnold’s Problems. Springer, PHASIS, Berlin, Moscow (2004)
- Barth [1996] Barth, W., Bauer, Th: Poncelet theorems. Exposition. Math. 14, 125–144 (1996)
- Baryshnikov and Zharnitsky [2006] Baryshnikov, Yu., Zharnitsky, V.: Sub-Riemannian geometry and periodic orbits in classical billiards. Math. Res. Lett. 13, 587–598 (2006)
- Bos et al. [1987] Bos, H., Kers, C., Oort, F., Raven, D.: Poncelet’s closure theorem. Expos. Math. 5, 289–364 (1987)
- Demaine et al. [2007] Demaine, E., O’Rourke, J.: Geometric Folding Algorithms. Linkages, Origami, Polyhedra. Cambridge University Press, Cambridge (2007)
- Demaine et al. [2011] Demaine, E., Demaine, M., Hart, V., Price, G., Tachi, T.: (Non)existence of pleated folds: how paper folds between creases. Graphs Combin. 27, 377–397 (2011)
- Dogru and Tabachnikov [2003] Dogru, F., Tabachnikov, S.: On polygonal dual billiard in the hyperbolic plane. Reg. Chaotic Dynam. 8, 67–82 (2003)
- Dogru and Tabachnikov [2005] Dogru, F., Tabachnikov, S.: Dual billiards. Math. Intell. 27(4), 18–25 (2005)
- Dragovic and Radnovic [2011] Dragovic, V., Radnovic, M.: Poncelet Porisms and Beyond. Integrable Billiards, Hyperelliptic Jacobians and Pencils of Quadrics. Birkhäuser, Basel (2011)
- Farber and Tabachnikov [2002] Farber, M., Tabachnikov, S.: Topology of cyclic configuration spaces and periodic orbits of multi-dimensional billiards. Topology 41, 553–589 (2002)
- Flatto [2009] Flatto, L.: Poncelet’s theorem. AMS, Providence, RI (2009)
- Foote et al. [2013] Foote, R., Levi, M., Tabachnikov, S.: Tractrices, bicycle tire tracks, hatchet planimeters, and a 100-year-old conjecture. Am. Math. Monthly 103, 199–216 (2013)
- Fuchs and Tabachnikov [1999] Fuchs, D., Tabachnikov, S.: More on paperfolding. Am. Math. Monthly 106, 27–35 (1999)
- Fuchs and Tabachnikov [2009] Fuchs, D., Tabachnikov, S.: Self-dual polygons and self-dual curves. Funct. Anal. Other Math. 2(2–4), 203–220 (2009)
- Genin et al. [2007] Genin, D., Khesin, B., Tabachnikov, S.: Geodesics on an ellipsoid in Minkowski space. Enseign. Math. (2) 53(3–4), 307–331 (2007)
- Ghomi and Tabachnikov [2008] Ghomi, M., Tabachnikov, S.: Totally skew embeddings of manifolds. Math. Z. 258, 499–512 (2008)
- Glutsyuk [2014] Glutsyuk, A.: On 4-reflective complex analytic planar billiards.
- Griffiths and Harris [1978] Griffiths, Ph, Harris, J.: On Cayley’s explicit solution to Poncelet’s porism. Enseign. Math. 24(1–2), 31–40 (1978)
- Kantor and Maydanskiy [2003] Kantor, J., Maydanskiy, M.: Triangles Gone Wild. MASS Selecta, pp. 277–288. American Mathematical Society, Providence (2003)
- Khesin and Tabachnikov [2009] Khesin, B., Tabachnikov, S.: Pseudo-Riemannian geodesics and billiards. Adv. Math. 221, 1364–1396 (2009)
- Levi and Tabachnikov [2009] Levi, M., Tabachnikov, S.: On bicycle tire tracks geometry, hatchet planimeter, Menzin’s conjecture and oscillation of unicycle tracks. Exp. Math. 18, 173–186 (2009)
- Monsky [1990] Monsky, P.: A conjecture of Stein on plane dissections. Math. Z. 205, 583–592 (1990)
- O’Rourke [2011] O’Rourke, J.: How to Fold it. The Mathematics of Linkages, Origami, and Polyhedra. Cambridge University Press, Cambridge (2011)
- Ovsienko et al. [2010] Ovsienko, V., Schwartz, R., Tabachnikov, S.: The Pentagram map: a discrete integrable system. Comm. Math. Phys. 299, 409–446 (2010)
- Schwartz [2009] Schwartz, R.: Obtuse triangular billiards. II. One hundred degrees worth of periodic trajectories. Exp. Math. 18, 137–171 (2009)
- Schwartz and Tabachnikov [2010] Schwartz, R., Tabachnikov, S.: Elementary surprises in projective geometry. Math. Intell. 32(3), 31–34 (2010)
- Stein and Szabo [1994] Stein, S., Szabo, S.: Algebra and Tiling. The Mathematical Association of America, Washington (1994)
- Tabachnikov [1994] Tabachnikov, S.: Commuting dual billiard maps. Geom. Dedicata 53, 57–68 (1994)
- Tabachnikov [1995] Tabachnikov, S.: On the dual billiard problem. Adv. Math. 115, 221–249 (1995)
- Tabachnikov [2003] Tabachnikov, S.: On three-periodic trajectories of multi-dimensional dual billiards. Alg. Geom. Topol. 3, 993–1004 (2003)
- Tabachnikov [2005] Tabachnikov, S.: Geometry and Billiards. American Mathematical Society, Providence (2005)
- Tabachnikov [2007] Tabachnikov, S.: A proof of Culter’s theorem on the existence of periodic orbits in polygonal outer billiards. Geom. Dedicata 129, 83–87 (2007)
- Tabachnikov [2008] Tabachnikov, S.: On algebraically integrable outer billiards. Pacific J. Math. 235, 89–92 (2008)