Arnold Mathematical Journal Problem Contribution

Received: 26.12.2014 / Accepted: 26.12.2014 / Published online: 21.1.2015

Periods of Pseudo-Integrable Billiards

Vladimir Dragović vladimir.dragovic@utdallas.edu , Milena Radnović The research was supported by Project 174020: Geometry and Topology of Manifolds, Classical Mechanics, and Integrable Dynamical Systems of the Serbian Ministry of Education, Science, and Technological Development and by Grant no. FL120100094 from the Australian Research Council.

Abstract

Consider billiard desks composed of two concentric half-circles connected with two edges. We examine billiard trajectories having a fixed circle concentric with the boundary semicircles as the caustic, such that the rotation numbers with respect to the half-circles are $\rho_1$ and $\rho_2$ respectively. Are such billiard trajectories periodic, and what are all possible periods for given $\rho_1$ and $\rho_2$?.

Keywords

Billiards, Rotation numbers, Periodic trajectories , Concentric circles

1 Introduction: Rotation Numbers

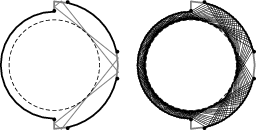
Let us start with the billiard within a circle $\mathcal{C}$. The trajectories of this system are polygonal lines inscribed in $\mathcal{C}$, having all sides of the same length. A natural and easy question is whether such a line is periodic. Namely, if $\alpha$ is the central angle of $\mathcal{C}$ corresponding to a chord of the length equal to a side of a given trajectory, then the trajectory is periodic if and only if $\dfrac{\alpha}{2\pi}$ is rational.

The number $\rho=\dfrac{\alpha}{2\pi}$ is called the rotation number. It is easy to see that the period is equal to $q$ if and only if the rotation number is equal to $\frac{s}{q}$, with $(s,q)=1$.

The numerator $s$ corresponds to the winding number---the number of rounds of the billiard particle about the centre within one period.


Figure 1: The billiard domain, one trajectory, and its caustic

Notice that there is a circle $\mathcal{C}_0$ concentric with $\mathcal{C}$, which is tangent to each segment of the given billiard trajectory. We will refer to $\mathcal{C}_0$ as the caustic of the trajectory.

If $R$ and $r$ are radii of $\mathcal{C}$ and $\mathcal{C}_0$ then the rotation number is: $$ \rho=\frac{1}{\pi}\arccos\frac{r}R. $$

2 Formulation of the Problem

Consider the billiard system within a domain bounded by two concentric half-circles and two segments lying on the same diameter, as shown in Fig. 1.

Each trajectory of such a billiard will also have a caustic which is concentric with the half-circles contained in the boundary.

Let $R_1$, $R_2$ be the radii of the half-circles on the boundary. For a fixed the caustic of radius $r$, denote by $\rho_1=\rho(R_1,r)$, $\rho_2=\rho(R_2,r)$ the corresponding rotation numbers.

Question 1. Given $\rho_1$, $\rho_2$, determine if the billiard trajectories are periodic. If yes, what are the periods?

3 Examples

Let us present several examples.

Example 1. Consider the billiard domain described in Sect. 2, and the caustic, such that the rotation numbers are $\rho_1=1/3$ and $\rho_2=1/4$. The boundary of that domain is decomposed into two regions, see Fig. 2. For each trajectory with the given caustic, we have:
  • either all bouncing points in the gray parts---in this case, the billiard particle hits twice each gray part until the trajectory becomes closed and the trajectory is $12$-periodic;
  • or all bouncing points are in the black parts---the particle will hit each part once until closure and the trajectory is $7$-periodic.

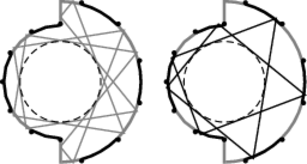
Figure 2: $12$-Periodic and $7$-periodic trajectories;
the decomposition of the boundary into two regions
Example 2.
  • For $\rho_1 = 1/4$, $\rho_2 = 1/6$, all billiard trajectories are periodic. They are divided into two classes, one containing the $5$-periodic trajectories and another containing the $6$-periodic ones.
  • If $\rho_1 = 1/3$, $\rho_2 = 1/5$, all billiard trajectories are again periodic. Their periods are equal to $13$ and $21$.
Example 3. For $\rho_1= 1/4$, $\rho_2=1/\sqrt{30}$, there exist both periodic and non-periodic trajectories. The boundary is again decomposed into two regions, as shown in Fig. 3. For each trajectory with the given caustic, we have:
  • either all bouncing points are in the black parts---in this case, the trajectory is not periodic;
  • or all bouncing points are in the gray parts---the particle will hit each part twice until the closure and the trajectory is $6$-periodic.

Figure 3: Both periodic and non-periodic
trajectories can share the same caustic

Now, we can reformulate the Question 1 in the following way:

Question 2. (Arithmetic Question) For given rotational numbers $\rho_1$ and $\rho_2$, find an arithmetic criterion to determine the number of non-periodic regions on the boundary, the number of periodic ones and the corresponding periods.
Question 3. We can ask Questions 1 and 2 in a more general situation: for a billiard domain bounded by a finite number of arcs of concentric circles and segments of the radial lines of the circles.

4 Final Remarks

Remark 1. There is an upper topological bound on the possible number $n+m$ of regions as a linear function of the total number $k$ of concave angles on the boundary of the billiard desk, see [Dragović and Radnović 2014a], [Dragović and Radnović 2014b]. For $k=1$ the upper bound is $3$ and for $k=2$ the upper bound is $6$.
Remark 2. The answers to the above questions remain the same for the billiards within domains bounded by arcs of confocal conics, see [Dragović and Radnović 2014a], [Dragović and Radnović 2014b]. For the definition of the rotation numbers associated to confocal conics see [Dragović and Radnović 2011], [King 1994], [Kozlov and Treshchёv 1991], [Tabachnikov 2005].
Remark 3. Analytical condition for periodicity of a billiard trajectory within an ellipse is a classical result of [Cayley 1853], [Griffiths and Harris 1978]. This result was generalized to domains bounded by several confocal conics [Dragović and Radnović 2004], [Dragović and Radnović 2011], when there are no reflex angles on the boundary. However, the result derived in [Dragović and Radnović 2004] can be applied also to the billiard domains with concave angles on the boundary, but only as a necessary condition.

Remark 4. The above examples show that so-called pseudo-integrable billiards within tables bounded by arcs of confocal conics and containing concave angles generate dynamics which is significantly different from the integrable dynamics. See [Dragović and Radnović 2014a], [Dragović and Radnović 2014b], [Richens and Berry 1981] for more details about pseudo-integrabilty. Qualitative picture of the integrable dynamics is encapsulated in the Liouville--Arnold theorem [Arnold 1978], according to which the non-degenerate compact invariant manifolds are tori. On each torus, the trajectories are either all periodic with the same period, or all non-periodic and dense. In contrast, in the case of of pseudo-integrable billiards with $k$ reflex angles, the invariant surfaces are of genus $g=k+1$, see [Dragović and Radnović 2014a], [Dragović and Radnović 2014b] and also [Maier 1943], [Zemljakov and Katok 1975], [Arnold 1992], [Arnold 1993]. In Examples 1--3, we had $k=2$ and thus $g=3$. Examples 1 and 2 show that the fixed invariant surface of genus $3$ can be decomposed into two regions with distinct periods. Example 3 shows the case of an invariant surface of genus $3$ decomposed into two regions, one with periodic and another with non-periodic trajectories.

References

  • [Arnold 1978] Arnold, V.I.: Mathematical Methods of Classical Mechanics. Springer, New York (1978)
  • [Arnold 1992] Arnold, V.I.: Poly-integrable flows. Algebra i Analiz 46, 54–62 (Russian, with Russian summary) (1992)
  • [Arnold 1993] Arnold, V.I.: English transl. St. Petersburg Math. J. 4(6), 1103–1110 (1993)
  • [Cayley 1853] Cayley, A.: Note on the porism of the in-and-circumscribed polygon. Philos. Mag. 6, 99–102 (1853)
  • [Dragović and Radnović 2004] Dragović, V., Radnović, M.: Cayley-type conditions for billiards within $k$ quadrics in $\mathbf{R}^d$. J. Phys. A Math. Gen. 37, 1269–1276 (2004)
  • [Dragović and Radnović 2011] Dragović, V., Radnović, M.: Poncelet Porisms and Beyond. Springer, Basel (2011)
  • [Dragović and Radnović 2014a] Dragović, V., Radnović, M.: Pseudo-integrable billiards and arithmetic dynamics. J. Mod. Dyn. (2014)
  • [Dragović and Radnović 2014b] Dragović, V., Radnović, M.: Bicentennial of the great Poncelet theorem (1813–2013): current advances. Bull. Am. Math. Soc. (N.S.) 51(3), 373–445 (2014)
  • [Griffiths and Harris 1978] Griffiths, P., Harris, J.: On Cayley's explicit solution to Poncelet's porism. Enseign. Math. 24(1–2), 31–40 (1978)
  • [King 1994] King, J.L.: Three problems in search of a measure. Am. Math. Mon. 101(7), 609–628 (1994)
  • [Kozlov and Treshchёv 1991] Kozlov, V., Treshchёv, D.: Billiards. American Mathematical Society, Providence (1991)
  • [Maier 1943] Maier, A.G.: Trajectories on closable orientable surfaces (Russian). Sb. Math. 12, 71–84 (1943)
  • [Richens and Berry 1981] Richens, P.J., Berry, M.V.: Pseudointegrable systems in classical and quantum mechanics. Physica D 2(3), 495–512 (1981)
  • [Tabachnikov 2005] Tabachnikov, S.: Geometry and Billiards, Student Mathematical Library, vol. 30. American Mathematical Society, Providence (2005)
  • [Zemljakov and Katok 1975] Zemljakov, A.N., Katok, A.B.: Topological transitivity of billiards in polygons (Russian). Mat. Zametki 18(2), 291–300 (1975)