Remarks on the Circumcenter of Mass
Abstract
Suppose that to every non-degenerate simplex $\Delta\subset{\mathbb{R}}^{n}$ a ‘center’ $C(\Delta)$ is assigned so that the following assumptions hold:
-
(i)
The map $\Delta\to C(\Delta)$ commutes with similarities and is invariant under the permutations of the vertices of the simplex;
-
(ii)
The map $\Delta\to\mathrm{Vol}(\Delta)C(\Delta)$ is polynomial in the coordinates of the vertices of the simplex.
Then $C(\Delta)$ is an affine combination of the center of mass $CM(\Delta)$ and the circumcenter $CC(\Delta)$ of the simplex:
| $C(\Delta)=tCM(\Delta)+(1-t)CC(\Delta),$ |
where the constant $t\in{\mathbb{R}}$ depends on the map $\Delta\mapsto C(\Delta)$ (and does not depend on the simplex $\Delta$). The motivation for this theorem comes from the recent study of the circumcenter of mass of simplicial polytopes by the authors and by A. Akopyan.
Keywords
1 Introduction
Given a homogeneous polygonal lamina $P$, one way to find its center of mass is as follows: triangulate $P$, assign to each triangle its centroid, taken with the weight equal to the area of the triangle, and find the center of mass of the resulting system of point masses. That the resulting point, $CM(P)$, does not depend on the triangulation, is a consequence of Archimedes’ Lemma: if an object is divided into smaller objects, then the center of mass of the compound object is the weighted average of the centers of mass of the parts, with the weights equal to the respective areas.
Replace, in the above construction, the centroids of the triangles by their circumcenters. The resulting weighted average is called the circumcenter of mass of the polygon $P$, denoted by $CCM(P)$. This point is well defined, that is, does not depend on the triangulation (assuming that degenerate triangles are avoided), see Fig. 1.
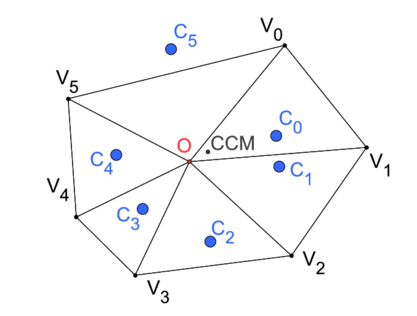
This construction is mentioned in the 19th century book ([Laisant1887]), where it is attributed to the Italian algebraic geometer G. Bellavitis. We learned about this reference from B. Grünbaum who, together with G. C. Shephard, studied this at about the same time, the circumcenter of mass was rediscovered by [Adler1993]; [Adler1995] as an integral of a discrete dynamical system called recutting of polygons.
The explicit formulas are as follows. Let the coordinates of the vertices of the polygon $P$, taken in the cyclic order, be $(x_{i},y_{i}),\ i=1,\ldots,n$. Then $CCM(P)=\frac{1}{4A(P)}\left(\sum_{i=0}^{n-1}y_{i}(x_{i-1}^{2}+y_{i-1}^{2}-x_{i+1}^{2} -y_{i+1}^{2}),\sum_{i=0}^{n-1}-x_{i}(x_{i-1}^{2}+y_{i-1}^{2}-x_{i+1}^{2}-y_{i+ 1}^{2})\right),$ where $A(P)$ is the signed area of $P$ (see [Tabachnikov and Tsukerman2014] for a proof). For comparison, $CM(P)=\frac{1}{6A(P)}\left(\sum_{i=0}^{n-1}(x_{i}+x_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i} ),\sum_{i=0}^{n-1}(y_{i}+y_{i+1})(x_{i}y_{i+1}-x_{i+1}y_{i})\right)$, a result of a straightforward calculation.
The construction of the circumcenter of mass extends to higher dimensions, and to the elliptic and hyperbolic geometries. We studied it in [Tabachnikov and Tsukerman2014] in relation with the so-called discrete bicycle transformation ([Tabachnikov and Tsukerman2013]). See also the paper by [Akopyan2014] .
The construction in ${\mathbb{R}}^{n}$ is similar. Given a simplicial polytope $P$, consider its non-degenerate triangulation. Assign the circumcenter $CC(\Delta_{i})$ to each simplex $\Delta_{i}$ of the triangulation, and take the center of mass of these points with weights equal to the oriented volumes of the respective simplices:
| $CCM(P)=\frac{1}{\mathrm{Vol}(P)}\sum_{i}\mathrm{Vol}(\Delta_{i})\ CC(\Delta_{i% }).$ | (1) |
The result does not depend on the triangulation.
The explicit formula is as follows. Let $F=(V_{1},\ldots,V_{n})$ be a face of $P$, where $V_{i}$ are vectors in ${\mathbb{R}}^{n}$. Let $A(F)$ be the $n\times n$ matrix made of vectors $V_{i}$, and let $A_{i}(F)$ be obtained from $A(F)$ by replacing $i$th row with $(|V_{1}|^{2},\ldots,|V_{n}|^{2})$. Then the $i$th component of the circumcenter of mass is given by
| $CCM(P)_{i}=\frac{1}{2(n!){\rm Vol}(P)}\sum_{F\subset\partial P}\det A_{i}(F).$ |
In the above formulas, the signs of $\mathrm{Vol}(\Delta_{i})$ and the orders of vertices $V_{1},\ldots,V_{n}$ are chosen consistently: we consider the triangulation as a simplicial chain.
One can take affine combinations $tCM+(1-t)CCM,\ t\in{\mathbb{R}}$, resulting in a line, called the generalized Euler line of the polytope $P$ (for a triangle, the Euler line is the line through the centroid and the circumcenter; it passes through the orthocenter as well).
In this note we are interested in the uniqueness of this construction.
Suppose that to every non-degenerate simplex $\Delta\subset{\mathbb{R}}^{n}$ a ‘center’ $C(\Delta)\in{\mathbb{R}}^{n}$ is assigned so that the following assumptions hold:
-
1.
The map $\Delta\mapsto C(\Delta)$ commutes with similarities (both orientation-preserving and orientation-reversing);
-
2.
The map $\Delta\mapsto C(\Delta)$ is invariant under the permutations of the vertices of the simplex $\Delta$;
-
3.
The map $\varphi:\Delta\mapsto\mathrm{Vol}(\Delta)C(\Delta)$ is polynomial in the coordinates of the vertices of the simplex $\Delta$;
Theorem 1.
Under these assumptions, $C(\Delta)$ is an affine combination of the center of mass and the circumcenter:
| $C(\Delta)=tCM(\Delta)+(1-t)CC(\Delta),$ |
where the constant $t\in{\mathbb{R}}$ depends on the map $\Delta\mapsto C(\Delta)$ (and does not depend on the simplex $\Delta$).
2 Basic Determinants
Let $x_{1},\ldots,x_{n}$ be Cartesian coordinates in ${\mathbb{R}}^{n}$. Let $\Delta=(V_{0},\ldots,V_{n})$ be a simplex, and let $V_{j}=(x_{1}^{j},\ldots,x_{n}^{j}),\ j=0,\ldots,n$, be the coordinates of its vertices (where $j$ is a superscript, not an exponent). Let
| $$ V=\left|\begin{matrix}x_{1}^{0}& x_{1}^{1}&\cdots& x_{1}^{n}\\ x_{2}^{0}& x_{2}^{1}&\cdots& x_{2}^{n}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n}^{0}&x_{n}^{1}&\cdots&x_{n}^{n}\\ 1&1&\cdots&1\end{matrix}\right|,$$ |
a multiple of the oriented volume of $\Delta$, and
| $X_{i,jk}$ | $\displaystyle=\left|\begin{matrix}x_{1}^{0} &x_{1}^{1}&\cdots&x_{1}^{n}\\ x_{2}^{0}&x_{2}^{1}&\cdots&x_{2}^{n}\\ \vdots&\vdots&\ddots&\vdots\\ x_{i-1}^{0}&x_{i-1}^{1}&\cdots&x_{i-1}^{n}\\ x_{j}^{0}x_{k}^{0}&x_{j}^{1}x_{k}^{1}&\cdots&x_{j}^{n}x_{k}^n \\ x_{i+1}^{0}&x_{i+1}^{1}&\cdots&x_{i+1}^{n}\\ \vdots&\vdots&\ddots&\vdots\\ x_{n}^{0}&x_{n}^{1}&\cdots&x_{n}^{n}\\ 1&1&\cdots&1\end{matrix}\right|$ | ||
| $\displaystyle=\text{Skew}(x_{1}^{0}x_{2}^{1}\cdots\widehat{x_{i}^{i-1}}\cdots x% _{n}^{n-1}x_{j}^{i-1}x_{k}^{i-1}),\quad 1\leq i,j,k\leq n.$ |
where Skew is skew-symmetrization over superscripts. Evidently, $X_{i,jk}=X_{i,kj}$, and the number of such polynomials equals $n^{2}(n+1)/2$. Both determinants, $V$ and $X_{i,jk}$, are skew-symmetric under permutations of the vertices of the simplex.
Lemma 2.1.
The polynomials $X_{i,jk}$ constitute a linear basis of the space ${\cal S}$ of homogeneous polynomials of degree $n+1$ in the variables $x_{1}^{0},x_{2}^{0},\ldots,x_{n}^{n}$, skew-symmetric under permutations of the superscripts.
Proof.
Since
| $X_{i,jk}=\text{Skew}(x_{1}^{0}x_{2}^{1}\cdots\widehat{x_{i}^{i-1}}\cdots x_{n}% ^{n-1}x_{j}^{i-1}x_{k}^{i-1}),$ |
a monomial $x_{1}^{0}x_{2}^{1}\cdots\widehat{x_{i}^{i-1}}\cdots x_{n}^{n-1}x_{j}^{i-1}x_{k% }^{i-1}$ determines $X_{i,jk}$. We will show that:
-
1.
There exists no nonidentity permutation acting on superscripts that maps this monomial to itself.
-
2.
These monomials lie in different orbits under this action.
The former shows that this monomial does not cancel in the expression of $X_{i,jk}$. The latter will then imply that different monomials give rise to different determinants.
Suppose that there exists a permutation $\sigma$ such that
| $x_{1}^{0}x_{2}^{1}\cdots\widehat{x_{i}^{i-1}}\cdots x_{n}^{n-1}x_{j}^{i-1}x_{k% }^{i-1}=x_{1}^{\sigma(0)}x_{2}^{\sigma(1)}\cdots\widehat{x_{i^{\prime}}^{% \sigma(i^{\prime}-1)}}\cdots x_{n}^{\sigma(n-1)}x_{j^{\prime}}^{\sigma(i^{% \prime}-1)}x_{k^{\prime}}^{\sigma(i^{\prime}-1)}.$ |
The superscripts $i-1$ and $\sigma(i^{\prime}-1)$ are the unique ones which occur twice. Therefore $\sigma(i^{\prime}-1)=i-1$. The corresponding subscripts are $j,k$ and $j^{\prime},k^{\prime}$, so that $\{j,k\}=\{j^{\prime},k^{\prime}\}$. Dividing both sides by $x_{j}^{i-1}x_{k}^{i-1}$, we get
| $x_{1}^{0}x_{2}^{1}\cdots\widehat{x_{i}^{i-1}}\cdots x_{n}^{n-1}=x_{1}^{\sigma(% 0)}x_{2}^{\sigma(1)}\cdots\widehat{x_{i^{\prime}}^{\sigma(i^{\prime}-1)}}% \cdots x_{n}^{\sigma(n-1)},$ |
so that $i=i^{\prime}$ and $\sigma$ is the identity.
Let $f\in{\cal S}$. Then $f$ is equal to its skew-symmetrization. Write $f$ in its monomial basis:
| $f(x_{1}^{0},\ldots,x_{n}^{n})=\sum c_{\beta}^{\alpha}x_{\beta}^{\alpha},\quad|% \alpha|=|\beta|=n+1.$ |
Consider the skew-symmetrization of a monomial $x_{\beta}^{\alpha}$. If some number appears in $\alpha$ with multiplicity 3 or greater, then $\alpha$ must be missing some two distinct numbers $i,j\in\{0,1,\ldots,n\}$. Each permutation $\sigma$ has a counterpart $\sigma(i\,j)$ of opposite sign which maps $x_{\beta}^{\alpha}$ to the same monomial. Therefore the skew-symmetrization of $x_{\beta}^{\alpha}$ in this case is zero.
Now suppose that $\alpha$ contains $n+1$ different elements of $\{0,1,\ldots,n\}$. Since the entries of $\beta$ are elements of $\{1,2,\ldots,n\}$, there exist some $\beta_{i}$ and $\beta_{j}$ with $i\neq j$ such that $\beta_{i}=\beta_{j}$. Each permutation $\sigma$ has a counterpart $\sigma(\alpha_{i}\,\alpha_{j})$ of opposite sign which maps $x_{\beta}^{\alpha}$ to the same element.
It follows that the only monomials appearing in $f$ are those for which $\alpha$ is a permutation of $(0,1,\ldots,\widehat{i-1},\ldots,n-1,i-1,i-1)$. Assume without loss of generality that $\alpha$ is of this form. Let $\alpha=(\alpha_{1},\alpha_{2},\ldots,\alpha_{n},\alpha_{n+1})$ and $\beta=(\beta_{1},\beta_{2},\ldots,\beta_{n},\beta_{n+1})$. Suppose that $\beta_{i_{1}}=\beta_{i_{2}}=\ldots=\beta_{i_{k}}$. For the monomial to not vanish under skew-symmetrization, the corresponding multiset $\alpha_{i_{1}},\alpha_{i_{2}},\ldots,\alpha_{i_{k}}$ cannot be invariant under any transpositions. Knowing the structure of $\alpha$, we see that this implies that $k=1,2$ or 3. If $k=2$, then $(\alpha_{i_{1}},\alpha_{i_{2}})=(i-1,i-1)$. If $k=3$ then $(\alpha_{i_{1}},\alpha_{i_{2}},\alpha_{i_{3}})=(i-1,i-1,q)$, with $q\neq i-1$. This proves the claim. $\square$
Consider the map $\varphi:\Delta\mapsto\mathrm{Vol}(\Delta)C(\Delta)$, and let $(y_{1},\ldots,y_{n})$ be its components. Our assumption 3 implies that each $y_{\ell},\ \ell=1,\ldots,n$, is a polynomial in the variables $x_{1}^{0},x_{2}^{0},\ldots,x_{n}^{n}$. The assumption 1, applied to scaling, implies that these polynomials are homogeneous of degree $n+1$, and the assumption 2 that they are skew-symmetric under permutations of the superscripts. Lemma 2.1 implies that
| $y_{\ell}=\sum A_{i,jk}^{\ell}X_{i,jk},\quad\ell=1,\ldots,n,$ |
where the coefficients $A_{i,jk}^{\ell}$ satisfy $A_{i,jk}^{\ell}=A_{i,kj}^{\ell}$. We always assume that summation is over repeated indices.
Example 2.2.
The center of mass and the circumcenter of mass correspond to the functions
| $y_{\ell}=\frac{1}{n+1}\sum X_{i,i\ell}\quad{\rm and}\quad y_{\ell}=\frac{1}{2}% \sum X_{\ell,ii},$ |
respectively. In terms of the coefficients, one has:
| $A_{i,jk}^{\ell}=\frac{1}{2(n+1)}(\delta_{ij}\delta_{lk}+\delta_{ik}\delta_{lj}% )\quad{\rm and}\quad A_{i,jk}^{\ell}=\frac{1}{2}\delta_{i\ell}\delta_{jk},$ | (2) |
where $\delta$ is the Kronecker symbol.
We now show that Archimedes’ Lemma is automatically satisfied for any choice of coefficients $A_{i,jk}^{\ell}$. Let $\Delta=(V_{0},\ldots,V_{n})$ be a simplex and $O$ a point. Consider the simplices
| $\Delta_{i}=(V_{0},\ldots,V_{i-1},O,V_{i+1},\ldots,V_{n}),\quad i=0,\ldots,n.$ |
Lemma 2.3.
For every choice of $i,j,k$, one has:
| $X_{i,jk}(\Delta)=\sum_{i=0}^{n}X_{i,jk}(\Delta_{i}).$ |
Proof.
Let $f:{\mathbb{R}}^{n}\to{\mathbb{R}}^{n}$ be a mapping. Expand the following $(n+2)\times(n+2)$-determinant by minors across the bottom row:
| \begin{multline*}0=\left|\begin{matrix}f(O)&f(V_{0})&f(V_{1})&\cdots&f(V_{n})\\ 1&1&1&\cdots&1\\ 1&1&1&\cdots&1\end{matrix}\right| =\left|\begin{matrix}f(V_{0})&f(V_{1})&\cdots&f(V_{n})\\ 1&1&\cdots&1\end{matrix}\right|\\ -\left|\begin{matrix}f(O)&f(V_{1})&\cdots&f(V_{n})\\ 1&1&\cdots&1\end{matrix}\right|+\ldots+(-1)^{n+1}\left|\begin{matrix} f(O)&f(V_{0})&\cdots&f(V_{n-1})\\ 1&1&\cdots&1\end{matrix}\right|.\end{multline*} |
Let
| $f(x_{1},\ldots,x_{n})=(x_{1},\ldots,x_{i-1},x_{j}x_{k},x_{i+1},\ldots,x_{n}).$ |
Then, taking the orientations of the simplices into account, the above equality for determinants yields the result. $\square$
Lemma 2.3 is a particular case of Archimedes’ Lemma: the triangulation is conical, obtained by connecting the origin to the vertices of the simplex. It is shown in [Tabachnikov and Tsukerman2014] that this particular conical case implies Archimedes’ Lemma for all triangulations without extra points on the boundary [see Sect. 4(i) for a discussion].
In the next section, we shall use assumption 1, namely, the fact that the map $\Delta\mapsto C(\Delta)$ commutes with parallel translations, rotations, and transpositions of coordinates, to conclude that the coefficients $A_{i,jk}^{\ell}$ must be affine combinations of the ones in (2).
3 Proof of Theorem
Introduce infinitesimal parallel translations in $r$th direction and rotations in the $p,q$-plane:
| $\xi_{r}=\frac{\partial}{\partial x_{r}},\quad\eta_{pq}=x_{p}\frac{\partial}{% \partial x_{q}}-x_{q}\frac{\partial}{\partial x_{p}},\quad p,q,r=1,\ldots,n.$ |
Let $\sigma$ denote a transposition of coordinates. The next lemma describes the action of these transformations on the polynomials $X_{i,jk}$.
Lemma 3.1.
One has
| $\begin{align}\sigma(X_{i,jk})&=-X_{\sigma(i),\sigma(j)\sigma(k)},\ \xi_{r}(X_{i,jk})=(% \delta_{ij}\delta_{rk}+\delta_{ik}\delta_{rj})V,\\ \eta_{pq}(X_{i,jk})&= \delta_{qj}X_{i,pk}+\delta_{qk}X_{i,pj}-\delta_{pi}X_{q, jk}-\delta_{pj}X_{i,qk}-\delta_{pk}X_{i,qj}+\delta_{qi}X_{p,jk}.\end{align}$ |
Proof.
The first equality follows from the fact that, along with the transposition of indices, exactly two rows of the determinant $X_{i,jk}$ are interchanged. For the second equality, notice that
| $\begin{align}X_{i,jk}=x_{j}x_{k}\frac{\partial}{\partial x_{i}}(V),\quad\frac{\partial}{% \partial x_{r}}(V)=0,\quad x_{j}\frac{\partial}{\partial x_{i}}(V)=\delta_{ij}V.\end{align}$ |
It follows that
| $\begin{align}\xi_{r}(X_{i,jk})&=\left[\frac{\partial}{\partial x_{r}},x_{j}x_{k}\frac{% \partial}{\partial x_{i}}\right](V)\!=\!\delta_{rj}\ x_{k}\frac{\partial}{% \partial x_{i}}(V)\!+\!\delta_{rk}\ x_{j}\frac{\partial}{\partial x_{i}}(V)\\ &=(\delta_{ij}\delta_{rk}+\delta_{ik}\delta_{rj})V.\end{align}$ |
The third equality is proved similarly. $\square$
The covariance of the map $\Delta\mapsto C(\Delta)$ with respect to rigid motions is expressed by the next equations on the coefficients $A_{i,jk}^{\ell}$.
Proposition 1.
For every transposition $\sigma$ of the indices $1,\ldots,n$, one has
| $A_{i,jk}^{\ell}=A_{\sigma(i),\sigma(j)\sigma(k)}^{\sigma(\ell)}.$ | (3) |
The covariance with respect to infinitesimal translations is given by
| $\sum A_{i,ir}^{\ell}=\frac{1}{2}\delta_{\ell r}\quad{\rm for\ all}\quad\ell,r,$ | (4) |
and with respect to infinitesimal rotations by
| $\displaystyle A_{a,qc}^{\ell}\delta_{pb}+A_{a,qb}^{\ell}\delta_{pc}-A_{p,bc}^{% \ell}\delta_{qa}-A_{a,pc}^{\ell}\delta_{qb}-A_{a,pb}^{\ell}\delta_{qc}+A_{q,bc% }^{\ell}\delta_{pa}$ | ||||
| $\displaystyle\quad-A_{a,bc}^{p}\delta_{\ell q}+A_{a,bc}^{q}\delta_{\ell p}=0,$ | (5) |
for all $a,b,c,p,q,\ell$.
Proof.
A transposition of coordinates is reflection in a hyperplane, and it changes the sign of $V$. According to Lemma 3.1, a transposition also changes the sign of the basic polynomials: $X_{i,jk}\mapsto-X_{\sigma(i),\sigma(j)\sigma(k)}$. Hence the covariance of the map $\Delta\mapsto C(\Delta)$ with respect to $\sigma$ implies the equality
| $\sum A_{i,jk}^{\ell}X_{\sigma(i),\sigma(j)\sigma(k)}=\sum A_{i,jk}^{\sigma(% \ell)}X_{i,jk}$ |
for all $\ell$. Since the polynomials $X_{i,jk}$ form a basis, for each term on the right, there is a matching term on the left:
| $A_{i,jk}^{\sigma(\ell)}=A_{\sigma(i),\sigma(j)\sigma(k)}^{\ell}.$ |
Renaming $\sigma(\ell)$ by $\ell$, we obtain (1)‣
To establish (4)‣, we use Lemma 3.1 to calculate:
| $\xi_{r}\left(\frac{y_{\ell}}{V}\right)=\sum A_{i,jk}^{\ell}(\delta_{ij}\delta_% {rk}+\delta_{ik}\delta_{rj})=\sum 2A_{i,ir}^{\ell}.$ |
On the other hand, $y_{\ell}/V$ is the $\ell$th component of the map $\Delta\mapsto C(\Delta)$, and the infinitesimal translation in the $r$th direction sends it to $\delta_{\ell r}$. By translation covariance, the above sum equals $\delta_{\ell r}$, as claimed.
Likewise, the infinitesimal rotation in the $p,q$-plane annihilates $y_{\ell}$ for $\ell$ distinct from $p,q$, and sends $y_{q}$ to $y_{p}$, and $y_{p}$ to $-y_{q}$; in short,
| $y_{\ell}\mapsto y_{p}\delta_{\ell q}-y_{q}\delta_{\ell p}.$ |
On the other hand, by Lemma 3.1,
| $\begin{align}\eta_{pq}(y_{\ell})&=\sum A_{i,jk}^{\ell}(\delta_{qj}X_{i,pk}\!+\!\delta_{qk}% X_{i,pj}\!-\!\delta_{pi}X_{q,jk}\!-\!\delta_{pj}X_{i,qk}\!-\!\delta_{pk}X_{i,% qj}\!+\!\delta_{qi}X_{p,jk})\\ &=2A_{i,qj}^{\ell}X_{i,pj}-A_{p,jk}^{\ell}X_{q,jk}-2A_{i,pj}^{\ell}X_{i,qj}+A% _{q,jk}^{\ell}X_{p,jk}.\end{align}$ |
Equate this to
| $y_{p}\delta_{\ell q}-y_{q}\delta_{\ell p}=\sum(A_{i,jk}^{p}\delta_{\ell q}-A_{% i,jk}^{q}\delta_{\ell p})X_{i,jk},$ |
and then, for fixed $a,b,c$, equate the coefficients in front of $X_{a,bc}$ in both expressions to obtain (5). $\square$
Now we need to solve the system of linear Eqs. (3) – (5) on the unknowns $A_{i,jk}^{\ell}$. We use (3) to reduce the number of variables.
Consider the following four cases. If $|\{i,j,k,\ell\}|=4$ then, applying an appropriate sequence of transpositions, we obtain: $A_{i,jk}^{\ell}=A^{1}_{2,34}=:t$. If $|\{i,j,k,\ell\}|=3$, then one has four sub-cases, and $A_{i,jk}^{\ell}$ is equal to
| $A^{1}_{1,23}=:u,\quad{\rm or}\quad A^{1}_{2,13}=:v,\quad{\rm or}\quad A^{2}_{3% ,11}=:w,\quad{\rm or}\quad A^{2}_{1,13}=:s.$ |
Likewise, if $|\{i,j,k,\ell\}|=2$, then one has five sub-cases, and $A_{i,jk}^{\ell}$ is equal to
| $A^{1}_{1,22}=:\phi,\quad{\rm or}\quad A^{1}_{2,12}=:\psi,\quad{\rm or}\quad A^% {2}_{1,11}=:\alpha,\quad{\rm or}\quad A^{1}_{1,12}=:\beta,\quad{\rm or}\quad A% ^{1}_{2,11}=:\gamma.$ |
Finally, if $|\{i,j,k,\ell\}|=1$, then $A_{i,jk}^{\ell}=A^{1}_{1,11}=:\nu$. Thus we have 11 unknowns.
Now the strategy is to consider particular cases of (5) and (4).
To start with, consider (1) with $\ell=q=b=c\neq p=a$. One obtains
| $-2A^{q}_{p,pq}+A^{q}_{q,qq}-A^{p}_{p,qq}=0,$ |
or $2\psi+\phi=\nu.$ Likewise, (4) with $\ell=r$ yields $(n-1)\psi+\nu=1/2.$ It follows that
| $\nu=\frac{1}{2}-(n-1)\psi,\quad\phi=\frac{1}{2}-(n+1)\psi.$ | (6) |
We pause to check against Example 2.2. For the center of mass,
| $\psi=\frac{1}{2(n+1)},\quad\nu=\frac{1}{n+1},$ |
and the rest of variables vanish; for the circumcenter of mass, $\phi=\nu=1/2,$ and the rest vanishes. In both cases, (6) holds.
To finish the Proof of Theorem 1, we need to show that all variables, except $\phi,\psi,\nu$, vanish. We proceed in a similar fashion: (1) with $\ell=q=a=b=c\neq p$ yields
| $\alpha+2\beta+\gamma=0,$ |
(1) with $\ell=q=c\neq p=a=b$ yields $\gamma=\alpha$. Hence $\beta=-\alpha$. Next, (4) with $\ell\neq r$ yields
| $(n-2)s+\alpha+\beta=0,$ |
hence $s=0$.
Next, (5) with $\ell=q=c$, but distinct from pairwise distinct $p,a,b$, yields $t=0$. It remains to eliminate $u,v,w$ and $\alpha$. Toward this, (5) with $\ell=q=c\neq p=b$ and distinct from $a$ yields
| $\gamma=v+w,\quad{\rm hence}\quad\alpha=v+w.$ |
Likewise, (5) with $\ell=q=c\neq p=a$ and distinct from $b$, yields
| $-s+\beta-u=0,\quad{\rm hence}\quad\alpha+u=0.$ |
Next, (5) with $\ell=q=c=a$, but distinct from pairwise distinct $p,b$, yields
| $u+v+s=0,\quad{\rm hence}\quad u+v=0,$ |
and (5) $\ell=q=c=b$, but distinct from pairwise distinct $p,a$, yields $2v+w=0.$ We have obtained four linear equations on $u,v,w,\alpha$, and the only solution of this system is zero. This completes the proof.
4 Final Remarks
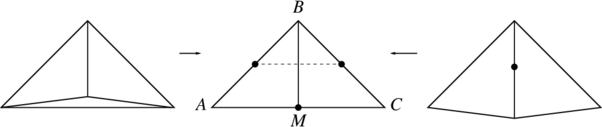
(i) Degenerate simplices can be safely ignored when calculating the center of mass: such a simplex has a finite centroid and zero volume, making no contribution to the total sum. Not so for the circumcenter of mass: although the volume of a nearly degenerate simplex tends to zero, its circumcenter may go to infinity, and the contribution to the sum (1) may be non-negligible. The map $\varphi:\Delta\mapsto\mathrm{Vol}(\Delta)\ CC(\Delta)$, being polynomial in the coordinates of the vertices, is continuous.
For example, consider an isosceles right triangle $ABC$. Its circumcenter is the midpoint $M$ of the hypothenuse $AC$. Consider the triangulation in Fig. 2 consisting of three triangles, one of which, $AMC$, is degenerate. If one ignored this triangle, then, by Archimedes’ Lemma, the circumcenter of mass of $\triangle ABC$ would be the midpoint of the segment connecting the midpoints of the hypothenuses $AB$ and $BC$ of the triangles $ABM$ and $BCM$. The latter point is the circumcenter of the quadrilateral $ABCM$, not the triangle $ABC$.
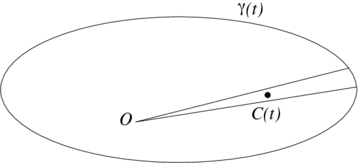
(ii) One may wish to extend the notion of the circumcenter of mass to more general sets. For example, let $\gamma(t)$ be a parameterized smooth curve, star-shaped with respect to point $O$, see Fig. 2. It is natural to define the circumcenter of mass by continuity as
| $\frac{\int{C}(t)\ dA}{\int dA},$ | (7) |
where $C(t)$ denotes the limiting $\varepsilon\to 0$ position of the vector from $O$ to the circumcenter of the infinitesimal triangle $O\gamma(t)\gamma(t+\varepsilon)$, and $dA$ is the area of this infinitesimal triangle. However, this does not give anything new: the integral (7) is the center of mass of the lamina bounded by the curve ([Tabachnikov and Tsukerman2014]).
(iii) Although the rational map $\Delta\mapsto CC(\Delta)$ is discontinuous, the polynomial map $\varphi:P\mapsto\mathrm{Vol}(P)\ CCM(P)$, defined on simplicial polytopes in ${\mathbb{R}}^{n}$, is continuous and is a valuation:
| $\varphi(P_{1}\cup P_{2})+\varphi(P_{1}\cap P_{2})=\varphi(P_{1})+\varphi(P_{2}).$ |
This valuation is isometry covariant; see, e.g., [Schneider2014] for the theory of valuations.
Continuity is with respect to the following topology in the space of polytopes in ${\mathbb{R}}^{n}$: if the vertices of a polytope $P$ are $V_{1},\ldots,V_{k}$, then we view $P$ as a point in ${\mathbb{R}}^{n}\times\ldots\times{\mathbb{R}}^{n}$ ($k$ times), and the topology is that of ${\mathbb{R}}^{nk}$.
(iv) We finish with open problems. Consider the same topology on the space of polytopes as in (iii).
Problem 4.1.
Describe the ${\mathbb{R}}^{n}$-valued continuous isometry covariant valuations on simplicial polytopes in ${\mathbb{R}}^{n}$.
As we mentioned, the construction of the circumcenter of mass extends to the spherical and hyperbolic geometries ([Akopyan2014]; [Tabachnikov and Tsukerman2014]). It is interesting to find an axiomatic description of the centers for simplicial polygons and polytopes, discussed in this note, in the three geometries of constant curvature (for the center of mass, see [Galperin1993]). These centers should be isometry covariant and satisfy some additivity condition (Archimedes’ Lemma or valuation-like). Such a description should include the valuations from Problem 4.1. At the moment of writing, we do not know such an axiomatic description.
Acknowledgements
References
- [Adler1993] Adler, V.: Cutting of polygons. Funct. Anal. Appl. 27, 141–143 (1993)
- [Adler1995] Adler, V.: Integrable deformations of a polygon. Phys. D 87, 52–57 (1995)
- [Akopyan2014] Akopyan, A.: Some remarks on the circumcenter of mass. Discret. Comput. Geom. 51, 837–841 (2014)
- [Galperin1993] Galperin, G.: A concept of the mass center of a system of material points in the constant curvature spaces. Commun. Math. Phys. 154, 63–84 (1993)
- [Hadwiger and Schneider1971] Hadwiger, H., Schneider, R.: Vektorielle Integralgeometrie. Elem. Math. 26, 49–57 (1971)
- [Laisant1887] Laisant, C.-A.: Théorie et applications des équipollences, pp. 150–151. Gauthier-Villars, Paris (1887)
- [Schneider2014] Schneider, R.: Convex bodies: the Brunn–Minkowski theory. Cambridge University Press, Cambridge (2014)
- [Tabachnikov and Tsukerman2013] Tabachnikov, S., Tsukerman, E.: On the discrete bicycle transformation. Publ. Math. Urug. (Proc. Montev. Dynam. Syst. Congr. 2012) 14, 201–220 (2013)
- [Tabachnikov and Tsukerman2014] Tabachnikov, S., Tsukerman, E.: Circumcenter of mass and generalized Euler line. Discret. Comput. Geom. 51, 815–836 (2014)