Homology of Spaces of Non-Resultant Homogeneous Polynomial Systems in ${\mathbb{R}}^{2}$ and ${\mathbb{C}}^{2}$
The resultant variety in the space of systems of homogeneous polynomials of some given degrees consists of such systems having non-trivial solutions. We calculate the integer cohomology groups of all spaces of non-resultant systems of polynomials ${\mathbb{R}}^{2}\to{\mathbb{R}}$, and also the rational cohomology rings of spaces of non-resultant systems and non-$m$-discriminant polynomials in ${\mathbb{C}}^{2}$.
Keywords
Configuration space, Caratheodory theorem
1 Introduction
Given $n$ natural numbers $d_{1}\geq d_{2}\geq\dots\geq d_{n}$, consider the space of all real homogeneous polynomial systems
| $\left\{{\!}\begin{aligned}\displaystyle a_{1,0}x^{d_{1}}+a_{1,1}x^{d_{1}-1}y+% \dots+a_{1,{d_{1}}}y^{d_{1}}\\ \displaystyle\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\dots\\ \displaystyle a_{n,0}x^{d_{n}}+a_{n,1}x^{d_{n}-1}y+\dots+a_{n,{d_{n}}}y^{d_{n}% }\\ \end{aligned}\right.$ | (1) |
in two real variables $x,y$.
We will refer to this space as ${\mathbb{R}}^{D}$, $D=\sum_{1}^{n}(d_{i}+1)$. The resultant variety $\Sigma\subset{\mathbb{R}}^{D}$ is the space of all systems having non-zero solutions. $\Sigma$ is a semialgebraic subvariety of codimension $n-1$ in ${\mathbb{R}}^{D}$.
Below we calculate the cohomology group of its complement, $H^{*}({\mathbb{R}}^{D}{\setminus}\Sigma)$. Also, we calculate the rational cohomology rings of the complex analogs ${\mathbb{C}}^{D}{\setminus}\Sigma_{\mathbb{C}}$ of all spaces ${\mathbb{R}}^{D}{\setminus}\Sigma$.
For the “affine” version of the “real” problem (concerning the space of non-resultant systems of polynomials ${\mathbb{R}}^{1}\to{\mathbb{R}}^{1}$ with leading terms $x^{d_{i}}$), see, e.g., [Vassiliev1994]; [Vassiliev1997] and [Kozlowski and Yamaguchi2000]; for the “complex” problem with $n=2$ see also [Cohen et al.1991]. A similar calculation for spaces of real homogeneous polynomials in ${\mathbb{R}}^{2}$ without zeros of multiplicity $\geq m$ was done in [Vassiliev1998].
The entire study of homology groups of spaces of non-singular (in appropriate sense) objects goes back to the Arnold’s works ([Arnold1970], [Arnold1989]), as well as the idea of using the Alexander duality in this problem.
2 Main Results
2.1 Notation
For any natural $p$, denote by $N(p)$ the sum of all numbers $d_{i}+1,$ $i=1,\dots,n,$ which are less than or equal to $p$, plus $p$ times the number of those $d_{i}$ which are equal to or greater than $p$. [In other words, $N(p)$ is the area of the part of Young diagram $(d_{1}+1,\dots,d_{n}+1)$ strictly to the left from the $(p+1)$-th column.] Let the index $\Upsilon(p)$ be equal to the number of even numbers $d_{i}\geq p$ if $p$ is even, and to the number of odd numbers $d_{i}\geq p$ if $p$ is odd. By $\tilde{H}^{*}(X)$ we denote the cohomology group reduced modulo a point. ${\overline{H}}_{*}(X)$ denotes the Borel–Moore homology group, i.e. the homology group of the complex of locally finite singular chains of $X$.
Theorem 1.
If the space ${\mathbb{R}}^{D}{\setminus}\Sigma$ is non-empty $($i.e. either $n>1$ or $d_{1}$ is even$)$, then the group $\tilde{H}^{*}({\mathbb{R}}^{D}{\setminus}\Sigma,{\mathbb{Z}})$ is equal to the direct sum of following groups:
A$)$ For any $p=1,\dots,d_{3}$,
if $\Upsilon(p)$ is even, then ${\mathbb{Z}}$ in dimension $N(p)-2p$ and ${\mathbb{Z}}$ in dimension $N(p)-2p+1$,
if $\Upsilon(p)$ is odd, then only one group ${\mathbb{Z}}_{2}$ in dimension $N(p)-2p+1$;
B$)$ If $d_{1}-d_{2}$ is odd, then an additional summand ${\mathbb{Z}}$ in dimension $D-d_{1}-d_{2}-2$. If $d_{1}-d_{2}$ is even, then an additional summand ${\mathbb{Z}}^{d_{2}-d_{3}+1}$ in dimension $D-d_{1}-d_{2}-1$ and $($if $d_{2}\neq d_{3})$ a summand ${\mathbb{Z}}^{d_{2}-d_{3}}$ in dimension $D-d_{1}-d_{2}-2$.
Example 1.
Let $n=2$ [so that part (A) in the statement of Theorem 1 is void]. If $d_{1}$ and $d_{2}$ are of the same parity, then ${\mathbb{R}}^{D}{\setminus}\Sigma$ consists of $d_{2}+1$ connected components, each of which is homotopy equivalent to a circle. For an invariant, which separates systems belonging to different components, we can take the index of the induced map of the unit circle $S^{1}\subset{\mathbb{R}}^{2}$ into ${\mathbb{R}}^{2}{\setminus}0$. This index can take all values of the same parity as $d_{1}$ and $d_{2}$ from the segment $[-d_{2},d_{2}]$. The 1-dimensional cohomology class inside any component is just the rotation number of the image of a fixed point [say, $(1,0)$] around the origin. Moreover, the images of this point under our non-resultant systems define a map ${\mathbb{R}}^{D}{\setminus}\Sigma\to{\mathbb{R}}^{2}{\setminus}0;$ it is easy to see that any fiber of this map consists of $d_{2}+1$ contractible components.
If $d_{1}$ and $d_{2}$ are of different parities, then the space ${\mathbb{R}}^{D}{\setminus}\Sigma$ has the homology of a two-point set. The invariant separating its two connected components can be calculated as the parity of the number of zeros of the odd-degree polynomial of our non-resultant system, which lie in the (well-defined) domain in ${\mathbb{RP}}^{1}$ where the even-degree polynomial is positive.
Now, let ${\mathbb{C}}^{D}$ be the space of all polynomial systems (1) with complex coefficients $a_{i,j}$, and $\Sigma_{\mathbb{C}}\subset{\mathbb{C}}^{D}$ the set of systems having solutions in ${\mathbb{C}}^{2}{\setminus}0$.
Theorem 2.
For any $n>1$, the ring $H^{*}({\mathbb{C}}^{D}{\setminus}\Sigma_{{\mathbb{C}}},{\mathbb{Q}})$ is an exterior algebra over ${\mathbb{Q}}$ with two generators of dimensions $2n-3$ and $2n-1$. Namely, these generators are the linking number with the Borel–Moore fundamental class of entire resultant variety and the pull-back of the basic cohomology class under the map ${\mathbb{C}}^{D}{\setminus}\Sigma_{\mathbb{C}}\to{\mathbb{C}}^{n}{\setminus}0$ defined by restrictions of non-resultant systems $(f_{1},\dots,f_{n})$ to the point $(1,0)$. The weight filtrations of these two generators and their product in the mixed Hodge structure of ${\mathbb{C}}^{D}{\setminus}\Sigma_{\mathbb{C}}$ are equal to $2n-2$, $2n$ and $4n-2$ respectively.
Consider also the space ${\mathbb{C}}^{d+1}$ of all complex homogeneous polynomials
| $a_{0}x^{d}+a_{1}x^{d-1}y+\dots+a_{d}y^{d}{,}$ |
and $m$-discriminant $\Sigma_{m}$ in it consisting of all polynomials vanishing on some line with multiplicity $\geq m$.
Theorem 3.
For any $m>1$ and $d\geq 2m-1$, the ring $H^{*}({\mathbb{C}}^{d+1}{\setminus}\Sigma_{m},{\mathbb{Q}})$ is isomorphic to an exterior algebra over ${\mathbb{Q}}$ with two generators of dimensions $2m-3$ and $2m-1$. The weight filtrations of these two generators and of their product are equal to $2m-2$, $2m$ and $4m-2$ respectively. For any $m>1$ and $d\in[m+1,2m-2]$, this ring is isomorphic to ${\mathbb{Q}}$ in dimensions $0,2m-3,2m-1$ and $2d-2$, and is trivial in all other dimensions; the multiplication is obviously trivial. For $d=m>1$ this ring is isomorphic to ${\mathbb{Q}}$ in dimensions 0 and $2m-3$, and is trivial in all other dimensions.
3 Some Preliminary Facts
Denote by $B(M,p)$ the configuration space of subsets of cardinality $p$ of a topological space $M$.
Lemma 1.
For any natural $p,$ there is a locally trivial fiber bundle $B(S^{1},p)\to S^{1}$ whose fiber is homeomorphic to ${\mathbb{R}}^{p-1}$. This fiber bundle is non-orientable if $p$ is even, and is orientable $($and hence trivial$)$ if $p$ is odd.
Indeed, the projection of this fiber bundle can be realised as the product of $p$ points of the unit circle in ${\mathbb{C}}^{1}$. The fiber of this bundle can be identified in terms of the universal covering ${\mathbb{R}}^{p}\to T^{p}$ with any connected component of some hyperplane $\{x_{1}+\dots+x_{p}=\mbox{const}\}$, from which all affine planes given by $x_{i}=x_{j}+2\pi k$, $i\neq j$, $k\in{\mathbb{Z}}$, are removed. Such a component is convex and hence diffeomorphic to ${\mathbb{R}}^{p-1}$. The assertion on orientability can be checked immediately. $\square$
Let us embed a manifold $M$ generically into the space ${\mathbb{R}}^{T}$ of a very large dimension, and denote by $M^{*r}$ the union of all $(r-1)$-dimensional simplices in ${\mathbb{R}}^{T}$, whose vertices lie in this embedded manifold (and the “genericity” of the embedding means that if two such simplices have a common point in ${\mathbb{R}}^{T}$, then their minimal faces containing this point coincide).
Proposition 1.
(C. Caratheodory theorem: see also [Vassiliev1997]; [Kallel and Karoui2011]) For any $r\geq 1$, the space $(S^{1})^{*r}$ is homeomorphic to $S^{2r-1}$.
Remark 1.
This homeomorphism can be realized as follows. Consider the space ${\mathbb{R}}^{2r+1}$ of all real homogeneous polynomials ${\mathbb{R}}^{2}\to{\mathbb{R}}^{1}$ of degree $2r$, the convex cone in this space consisting of everywhere non-negative polynomials, and (also convex) dual cone in the dual space $\widehat{\mathbb{R}}^{2r+1}$ consisting of linear forms taking only positive values inside the previous cone. The intersection of the boundary of this dual cone with the unit sphere in $\widehat{\mathbb{R}}^{2r+1}$ is naturally homeomorphic to $(S^{1})^{*r}$; on the other hand it is homeomorphic to the boundary of a convex $2r$-dimensional domain.
Lemma 2.
(see [Vassiliev1999], Lemma 3) For any $r>1$, the group $H_{*}((S^{2})^{*r},{\mathbb{Q}})$ is trivial in all positive dimensions. $\square$
Consider the “sign local system” $\pm{\mathbb{Q}}$ over $B({\mathbb{CP}}^{1},p)$, i.e. the local system of groups with fiber ${\mathbb{Q}}$ such that the elements of $\pi_{1}(B({\mathbb{CP}}^{1},p))$ defining odd (respectively, even) permutations of $p$ points in ${\mathbb{CP}}^{1}$ act in the fiber as multiplication by $-1$ (respectively, by 1).
Lemma 3.
(see [Vassiliev1999], Lemma 2) All Borel–Moore homology groups $\overline{H}_{i}(B({\mathbb{CP}}^{1},p);\pm{\mathbb{Q}})$ with $p\geq 1$ are trivial except
| $\overline{H}_{0}(B({\mathbb{CP}}^{1},1),\pm{\mathbb{Q}})\,{\cong}\,\overline{H% }_{2}(B({\mathbb{CP}}^{1},1),\pm{\mathbb{Q}})\,{\cong}\,\overline{H}_{2}(B({% \mathbb{CP}}^{1},2),\pm{\mathbb{Q}})\,{\cong}\,{\mathbb{Q}}.$ |
$\square$
4 Proof of Theorem 1
Following [Arnold1970], we use the Alexander duality
| $\tilde{H}^{i}({\mathbb{R}}^{D}{\setminus}\Sigma)\simeq{\overline{H}}_{D-i-1}(% \Sigma).$ | (2) |
4.1 Simplicial Resolution of $\Sigma$
To calculate the right-hand group in (2), we construct a resolution of the space $\Sigma$. Let $\chi:{\mathbb{RP}}^{1}\to{\mathbb{R}}^{T}$ be a generic embedding, $T\gg d_{1}$. For any system $\Phi=(f_{1},\dots,f_{n})\in\Sigma$ not equal identically to zero, consider the simplex $\Delta(\Phi)$ in ${\mathbb{R}}^{T}$ spanned by the images $\chi(x_{i})$ of all points $x_{i}\in{\mathbb{RP}}^{1}$ corresponding to all lines, on which the system $f$ has a common root. (The maximal possible number of such lines is obviously equal to $d_{1}.$)
Furthermore, consider a subset in the direct product ${\mathbb{R}}^{D}\times{\mathbb{R}}^{T}$, namely, the union of all simplices of the form $\Phi\times\Delta(\Phi),$ $\Phi\in\Sigma{\setminus}0$. This union is not closed: the set of its limit points not belonging to it is the product of the point $0\in{\mathbb{R}}^{D}$ (corresponding to the zero system) and the union of all simplices in ${\mathbb{R}}^{T}$ spanned by the images of no more than $d_{1}$ different points of the line ${\mathbb{RP}}^{1}.$ By the Caratheodory theorem, the latter union is homeomorphic to the sphere $S^{2d_{1}-1}.$ We can assume that our embedding $\chi:{\mathbb{RP}}^{1}\to{\mathbb{R}}^{T}$ is algebraic, and hence this sphere is semialgebraic. Take a generic $2d_{1}$-dimensional semialgebraic disc in ${\mathbb{R}}^{T}$ bounded by this sphere (e.g., the union of segments connecting the points of this sphere with a generic point in ${\mathbb{R}}^{T}$), and add the product of the point $0\in{\mathbb{R}}^{D}$ and this disc to the previous union of simplices $\Phi\times\Delta(\Phi)\subset{\mathbb{R}}^{D}\times{\mathbb{R}}^{T}$. The resulting closed subset in ${\mathbb{R}}^{D}\times{\mathbb{R}}^{T}$ will be denoted by $\sigma$ and called a simplicial resolution of $\Sigma$.
Lemma 4.
The obvious projection $\sigma\to\Sigma$ (induced by the projection of ${\mathbb{R}}^{D}\times{\mathbb{R}}^{T}$ onto the first factor) is proper, and the induced map between one-point compactifications of these spaces is a homotopy equivalence.
This follows easily from the fact that this projection is a stratified map of semialgebraic spaces, and the preimage of any point of $\Sigma$ is contractible: see [Vassiliev1994]; [Vassiliev1997]. $\square$
So, we can (and will) calculate the group ${\overline{H}}_{*}(\sigma)$ instead of ${\overline{H}}_{*}(\Sigma)$.
Remark 2.
There is a different construction of a simplicial resolution of $\Sigma$ in terms of “Hilbert schemes”. Namely, let $I_{p}$ be the space of all ideals of codimension $p$ in the space of smooth functions ${\mathbb{RP}}^{1}\to{\mathbb{R}}^{1}$ equipped with the natural “Grassmannian” topology. It is easy to see that $I_{p}$ is homeomorphic to the $p$-th symmetric power $S^{p}({\mathbb{RP}}^{1})=({\mathbb{RP}}^{1})^{p}/S(p){;}$ in particular, it contains the configuration space $B({\mathbb{RP}}^{1},p)$ as an open dense subset. Consider the disjoint union of these $d_{1}$ spaces $I_{1},\dots,I_{d_{1}}$ augmented with the one-point set $I_{\infty}$ symbolizing the zero ideal. The incidence of ideals makes this union a partially ordered set. Consider the continuous order complex $\Xi_{d_{1}}$ of this poset, i.e. the subset in the join $I_{1}*\dots*I_{d_{1}}*I_{\infty}$ consisting of simplices, whose all vertices are incident to one another. For any polynomial system $\Phi=(f_{1},\dots,f_{n})\in{\mathbb{R}}^{D}$, denote by $\Xi(\Phi)$ the subcomplex in $\Xi_{d_{1}}$ consisting of all simplices, whose all vertices correspond to ideals containing all polynomials $f_{1},\dots,f_{n}$. The simplicial resolution $\tilde{\sigma}\subset\Sigma\times\Xi_{d_{1}}$ is defined as the union of simplices $\Phi\times\Xi(\Phi)$ over all $\Phi\in\Sigma$.
This construction is homotopy equivalent to the previous one. In particular, the Caratheodory theorem has the following version (see [Kallel and Karoui2011]): the continuous order complex of the poset of all ideals of codimension $\leq r$ in the space of functions $S^{1}\to{\mathbb{R}}^{1}$ is homotopy equivalent to $S^{2r-1}$.
However, this construction is less convenient for our practical calculations than the one described above and used previously in [Vassiliev1994]; [Vassiliev1999] [and extended to some more complicated situations in [Gorinov2005]].
The space $\sigma$ has a natural increasing filtration $F_{1}\subset\dots\subset F_{d_{1}+1}=\sigma$: its term $F_{p},$ $p\leq d_{1},$ is the closure of the union of all simplices of the form $\Phi\times\Delta(\Phi)$ over all polynomial systems $\Phi$ having no more than $p$ lines of common zeros. Alternatively, it can be described as the union of all no more than $(p-1)$-dimensional faces of all simplices $\Phi\times\Delta(\Phi)$ over all systems $\Phi\in\Sigma{\setminus}0$, completed with all no more than $(p-1)$-dimensional simplices spanning some $\leq p$ points of the manifold $\{0\}\times\chi(\mathbb{RP}^{1})$.
Lemma 5.
For any $p=1,\ldots,d_{1},$ the term $F_{p}{\setminus}F_{p-1}$ of our filtration is the space of a locally trivial fiber bundle over the configuration space $B({\mathbb{RP}}^{1},p),$ with fibers equal to the direct product of a $(p-1)$-dimensional open simplex and a $(D-N(p))$-dimensional real space. The corresponding bundle of open simplices is orientable if and only if $p$ is odd $($i.e. exactly when the base configuration space is orientable$)$, and the bundle of $(D-N(p))$-dimensional spaces is orientable if and only if the index $\Upsilon(p)$ is even.
The last term $F_{d_{1}+1}{\setminus}F_{d_{1}}$ of this filtration is homeomorphic to an open $2d_{1}$-dimensional disc.
Indeed, to any configuration $(x_{1},\ldots,x_{p})\in B({\mathbb{RP}}^{1},p),$ $p\leq d_{1}$, there corresponds the direct product of the interior part of the simplex in ${\mathbb{R}}^{T}$ spanned by the images $\chi(x_{i})$ of points of this configuration, and the subspace of ${\mathbb{R}}^{D}$ consisting of polynomial systems that have solutions on corresponding $p$ lines in ${\mathbb{R}}^{2}.$ The codimension of the latter subspace is equal exactly to $N(p)$. The assertion concerning the orientations can be checked in a straightforward way. The description of $F_{d_{1}+1}{\setminus}F_{d_{1}}$ follows immediately from the construction and the Caratheodory theorem. $\square$
Consider the spectral sequence $E_{p,q}^{r},$ calculating the group ${\overline{H}}_{*}(\Sigma)$ and generated by this filtration. Its term $E_{p,q}^{1}$ is canonically isomorphic to the group ${\overline{H}}_{p+q}(F_{p}{\setminus}F_{p-1}).$ By Lemma 5, its column $E_{p,*}^{1},$ $p\leq d_{1},$ is as follows. If $\Upsilon(p)$ is even, then this column contains exactly two non-trivial terms $E_{p,q}^{1}$, both isomorphic to ${\mathbb{Z}}$, for $q$ equal to $D-N(p)+p-1$ and $D-N(p)+p-2$. If $\Upsilon(p)$ is odd, then this column contains only one non-trivial term $E_{p,q}^{1}$ isomorphic to ${\mathbb{Z}}_{2}$, for $q=D-N(p)+p-2$. Finally, the column $E^{1}_{d_{1}+1,*}$ contains only one non-trivial element $E^{1}_{d_{1}+1,d_{1}-1}\,{\cong}\,{\mathbb{Z}}$.
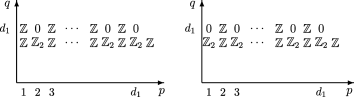
Before calculating the differentials and further terms $E^{r}$, $r>1$, let us consider several basic examples.
4.2 The Case $n=1$
If our system consists of only one polynomial of degree $d_{1}$, then the term $E^{1}$ of our spectral sequence looks as in Fig. 1; in particular, all non-trivial groups $E_{p,q}^{1}$ lie in two rows $q=d_{1}$ and $q=d_{1}-1$.
Lemma 6.
If $n=1$, then in both cases of even or odd $d_{1}$, all possible horizontal differentials $\partial_{1}:E_{p,d_{1}-1}^{1}\to E_{p-1,d_{1}-1}^{1}$ of the form ${\mathbb{Z}}\to{\mathbb{Z}}_{2}$, $p=d_{1}+1,d_{1}-1,d_{1}-3,\dots$ are epimorphisms, and all differentials $\partial_{2}:E_{p,d_{1}-1}^{2}\to E_{p-2,d_{1}}^{2}$ of the form ${\mathbb{Z}}\to{\mathbb{Z}}$, $p=d_{1}+1,d_{1}-1,d_{1}-3,\dots$ are isomorphisms. In particular, the unique surviving term $E_{p,q}^{3}$ for the “even” spectral sequence is $E_{1,d_{1}-1}^{3}\,{\cong}\,{\mathbb{Z}}$, and for the “odd” one it is $E_{2,d_{1}-1}^{3}\,{\cong}\,{\mathbb{Z}}$.
Indeed, in both cases we know the answer. In the “odd” case, the discriminant coincides with entire ${\mathbb{R}}^{D}={\mathbb{R}}^{d_{1}+1}$. In the “even” case, its complement consists of two contractible components, so that ${\overline{H}}_{*}(\Sigma)={\mathbb{Z}}$ in dimension $d_{1}$ and is trivial in all other dimensions. Therefore, all terms $E_{p,q}$ with $p+q$ not equal to $d_{1}+1$ (respectively, to $d_{1}$) in the odd- (respectively, even-) dimensional case should die at some stage; this is possible only if all assertions of our lemma hold. $\square$
4.3 The Case $n=2$
There are two very different situations depending on the parity of $d_{1}-d_{2}$. In Fig. 2, we demonstrate these situations in two particular cases: $(d_{1},d_{2})=(6,3)$ and $(7,3)$. However, the general situation is essentially the same; namely, the following is true.

If $n=2$ and $d_{1}-d_{2}$ is odd, then all indices $\Upsilon(p)$, $p=1,\dots,d_{2}+1$, are odd, and hence all non-trivial groups $E_{p,q}^{1}$ with such $p$ lie on the line $\{p+q=d_{1}+d_{2}\}$ only and are equal to ${\mathbb{Z}}_{2}$.
If $n=2$ and $d_{1}-d_{2}$ is even, then all indices $\Upsilon(p)$, $p=1,\dots,d_{2}+1$, are even, and hence all non-trivial groups $E_{p,q}^{1}$ with such $p$ lie on two lines $\{p+q=d_{1}+d_{2}\}$, $\{p+q=d_{1}+d_{2}+1\}$, and are all equal to ${\mathbb{Z}}$.
In both cases, all groups $E_{p,q}^{1}$ with $p>d_{2}$ are the same as in the case $n=1$ with the same $d_{1}$. Moreover, the differentials $\partial_{1}$ and $\partial_{2}$ between these groups are also the same as for $n=1$; therefore, all of these groups die at $E^{3}$ except for $E_{d_{2}+1,d_{1}-1}^{3}\,{\cong}\,{\mathbb{Z}}$ for even $d_{1}-d_{2}$, and $E_{d_{2}+2,d_{1}-1}^{3}\,{\cong}\,{\mathbb{Z}}$ for odd $d_{1}-d_{2}$.
In the case of even $d_{1}-d_{2}$, all other differentials between the groups $E_{p,q}^{r}$ are trivial, because otherwise the group $\tilde{H}^{0}({\mathbb{R}}^{D}{\setminus}\Sigma)$ would be smaller than ${\mathbb{Z}}^{d_{2}}$, in contradiction to $d_{2}+1$ different components of this space indicated in Example 1.
On the contrary, if $d_{1}-d_{2}$ is odd, then all the differentials $d_{r}:E_{d_{2}+2,d_{1}-1}^{r}\to E_{d_{2}+2-r,d_{1}-2+r}^{r}$, $r=1,\dots,d_{1}-d_{2}+1$, are epimorphic just because the integer cohomology group of the topological space ${\mathbb{R}}^{D}{\setminus}\Sigma$ cannot have non-trivial torsion subgroup in dimension 1. Therefore, the unique nontrivial group $E_{p,q}^{\infty}$ in this case is $E_{d_{2}+2,d_{1}-1}^{\infty}\,{\cong}\,{\mathbb{Z}}$.
This proves Theorem 1 for $n=2$.
4.4 The General Case
Now suppose that our systems (1) consist of $n\geq 3$ polynomials. Let again $\sigma$ be the simplicial resolution of the corresponding resultant variety constructed in Sect. 4.1, and $\sigma^{\prime}$ be the simplicial resolution of the resultant variety for $n=2$ and the same $d_{1}$ and $d_{2}$. The parts $\sigma{\setminus}F_{d_{3}}(\sigma)$ and $\sigma^{\prime}{\setminus}F_{d_{3}}(\sigma^{\prime})$ of these resolutions are canonically homeomorphic to one another as filtered spaces. In particular, $E_{p,q}^{1}(\sigma)=E_{p,q}^{1}(\sigma^{\prime})$ if $p>d_{3}$, and $E_{p,q}^{r}(\sigma)=E_{p,q}^{r}$ if $p\geq d_{3}+r$. All non-trivial terms $E_{p,q}^{r}(\sigma)$ with $p\leq d_{3}$ are placed in such a way that no non-trivial differentials $\partial_{r}$ can act between these terms, as well as no differentials can act to these terms from the cells $E_{p,q}^{r}$ with $p>d_{3}$, which have survived the differentials between these cells described in the previous subsection.
Therefore, the final term $E_{p,q}^{\infty}(\sigma)$ coincides with $E_{p,q}^{1}(\sigma)$ in the domain $\{p\leq d_{3}\}$, and coincides with the term $E_{p,q}^{\infty}(\sigma^{\prime})$ of the truncated spectral sequence calculating the Borel–Moore homology of $\sigma^{\prime}{\setminus}F_{d_{3}}(\sigma^{\prime})$ in the domain $\{p>d_{3}\}$. This completes the proof of Theorem 1. $\square$
5 Proof of Theorem 2
The simplicial resolution $\sigma_{{\mathbb{C}}}$ of $\Sigma_{{\mathbb{C}}}$ appears in the same way as its real analog $\sigma$ in the previous section. It also has a natural filtration $F_{1}\subset\dots\subset F_{d_{1}+1}=\sigma_{{\mathbb{C}}}$. For $p\in[1,d_{1}]$, its term $F_{p}{\setminus}F_{p-1}$ is fibered over the configuration space $B({\mathbb{CP}}^{1},p)$; its fiber over a configuration $(x_{1},\dots x_{p})$ is equal to the product of the space ${\mathbb{C}}^{D-N(p)}$ (consisting of all complex systems (1) vanishing at all lines corresponding to the points of this configuration) and the $(p-1)$-dimensional simplex whose vertices correspond to the points of the configuration. In particular, our spectral sequence calculating rational Borel-Moore homology of $\sigma_{{\mathbb{C}}}$ has $E^{1}_{p,q}\,{\cong}\,{\overline{H}}_{q-2(D-N(p))+1}(B({\mathbb{CP}}^{1},p);% \pm{\mathbb{Q}})$ for such $p$. By Lemma 3, only the following such groups are non-trivial: $E^{1}_{1,2(D-n)-1}\,{\cong}\,{\mathbb{Q}}$, $E^{1}_{1,2(D-n)+1}\,{\cong}\,{\mathbb{Q}}$, and (if $d_{1}>1$) $E^{1}_{2,2(D-2n)+1}\,{\cong}\,{\mathbb{Q}}$.
The last term $F_{d_{1}+1}{\setminus}F_{d_{1}}$ is homeomorphic to the cone over the $d_{1}$-th self-join $({\mathbb{CP}}^{1})^{*d_{1}}$ with the base of this cone removed (as it belongs to $F_{d_{1}}$). Therefore, by Lemma 2, the column $E^{1}_{d_{1}+1,*}$ is trivial if $d_{1}>1$, and contains a unique non-trivial group $E^{1}_{2,1}\,{\cong}\,{\mathbb{Q}}$ if $d_{1}=1$.
So, in any case, the first sheet $E^{1}$ of our spectral sequence has only three non-trivial terms $E^{1}_{1,2(D-n)-1}$, $E^{1}_{1,2(D-n)+1}$, and $E^{1}_{2,2(D-2n)+1}$, all of which are isomorphic to ${\mathbb{Q}}$. The differentials in it are obviously trivial; therefore, the group ${\overline{H}}_{*}(\sigma)$ has three non-trivial terms in dimensions $2(D-n)$, $2(D-n)+2$, and $2(D-2n)+3$. By Alexander duality in the space ${\mathbb{C}}^{D}$, this gives us three groups $\tilde{H}^{2n-3}\,{\cong}\,{\mathbb{Q}}$, $\tilde{H}^{2n-1}\,{\cong}\,{\mathbb{Q}}$, and $\tilde{H}^{4n-4}\,{\cong}\,{\mathbb{Q}}$, and zero in all other dimensions.
All assertions of Theorem 2 concerning the ring structure, realization of cohomology classes, and the weight filtration are well-known or obvious in the case $d_{1}=1$ (when $D=2n$ and ${\mathbb{C}}^{2n}{\setminus}\Sigma_{\mathbb{C}}$ is the space of pairs of linearly independent vectors in ${\mathbb{C}}^{n}$, and is homotopy equivalent to the Stiefel manifold $V_{2}({\mathbb{C}}^{n})$). The general case can be deduced from this one by the map $P:{\mathbb{C}}^{2n}{\setminus}\Sigma_{\mathbb{C}}\to{\mathbb{C}}^{D}{\setminus% }\Sigma_{\mathbb{C}}$ sending any collection of linear functions $(f_{1},\dots,f_{n})$ to $(f_{1}^{d_{1}},\dots,f_{n}^{d_{n}})$. Indeed, the realization of $(2n-1)$-dimensional classes follows from the commutative diagram
| $\require{AMScd}\begin{CD} {\mathbb{C}}^{2n}{\setminus}\Sigma_{\mathbb{C}}@>P>>{\mathbb{C}}^{D}{\setminus}\Sigma_{\mathbb{C}}\\ @VVV @VVV\\ {\mathbb{C}}^{n}{\setminus}0 @>>>{\mathbb{C}}^{n}{\setminus}0\end{CD},$ |
where the lower horizontal arrow is defined by
| $(z_{1},\dots,z_{n})\mapsto(z_{1}^{d_{1}},\dots,z_{n}^{d_{n}})$ |
and induces an isomorphism of $(2n-1)$-dimensional rational homology groups. The assertion on the realization of $(2n-3)$-dimensional classes is obvious. The statements on the multiplication and the weight filtration follow from the naturality of these structures. $\Box$
6 Proof of Theorem 3
The additive part of this theorem can be proved in almost the same way as that of Theorem 1: see [Vassiliev1998]. In particular, we construct a simplicial resolution $\sigma_{m}$ of the $m$-discriminant variety $\Sigma_{m}$. It has a natural filtration $\Phi_{1}\subset\dots\subset\Phi_{[d/m]}\subset\Phi_{[d/m]+1}=\sigma_{m}$. The term $\Phi_{p}{\setminus}\Phi_{p-1}$, $p\leq[d/m]$, of this filtration is the space of a fiber bundle with the base $B(\mathbb{CP}^{1},p)$. Its fiber over the collection of points $(z_{1},\dots,z_{p})\subset\mathbb{CP}^{1}$ is the product of an open $(p-1)$-dimensional simplex whose vertices are related with these $p$ points, and the subspace of codimension $mp$ in ${\mathbb{C}}^{d+1}$ consisting of all polynomials having $m$-fold zeros on the corresponding $p$ lines. The term $\Phi_{[d/m]+1}{\setminus}\Phi_{[d/m]}$ appears from the zero polynomial and is the cone over the space $(\mathbb{CP}^{1})^{*[d/m]}$ with the base of this cone removed. The term $E^{1}$ of the corresponding spectral sequence can be calculated immediately with the help of Lemmas 2 and 3. Its shape implies that all further differentials of the spectral sequence are trivial, with unique exception in the case $d=m$, when all non-zero (isomorphic to ${\mathbb{Q}}$) groups of $E^{1}$ are $E^{1}_{1,3}$, $E^{1}_{1,1}$, and $E^{1}_{2,1}$. In this case, the differential $\partial_{1}:E^{1}_{2,1}\to E^{1}_{1,1}$ is an isomorphism, because the zero section of the tautological bundle over ${\mathbb{CP}}^{1}$ defines a non-zero element of the 2-dimensional Borel–Moore homology group of the space of this bundle. Therefore, the only surviving term is $E^{2}_{1,3}\,{\cong}\,{\mathbb{Q}}$; by Alexander duality, it gives us a $(2m-3)$-dimensional cohomology class.
The remaining statements of Theorem 3 are based on the following comparison lemma. Consider the map $J:{\mathbb{C}}^{d+1}\to{\mathbb{C}}^{D}$, $D=m(d+2-m),$ sending any homogeneous polynomial ${\mathbb{C}}^{2}\to{\mathbb{C}}^{1}$ of degree $d$ to the collection of all its partial derivatives of order $m-1$.
Lemma 7.
For any $d\geq m>1$, $\Sigma_{m}=J^{-1}(\Sigma_{\mathbb{C}})$. For any $d\geq 2m-1$, the induced map of cohomology groups, $J^{*}:H^{*}({\mathbb{C}}^{D}{\setminus}\Sigma_{\mathbb{C}},{\mathbb{Q}})\to H^% {*}({\mathbb{C}}^{d+1}{\setminus}\Sigma_{m},{\mathbb{Q}}),$ is an isomorphism.
This is a standard comparison theorem of our spectral sequences: see especially Section IV.7 in [Vassiliev1994]; [Vassiliev1997]. $\square$
Now the assertions of Theorem 3 on the multiplication and weight filtrations follow from the similar assertions of Theorem 2 by the naturality of these structures. $\square$
Acknowledgements
I thank O. A. Malinovskaya for a useful discussion, and also the referee for suggesting to include the assertions on Hodge structure in Theorems 2 and 3.References
- [Arnold1970] Arnold, V.I.: On some topological invariants of algebraic functions. Trans. Moscow Math. Soc. 21, 30–52 (1970)
- [Arnold1989] Arnold, V.I.: Spaces of functions with moderate singularities. Funct. Anal. Appl. 23(3), 1–10 (1989)
- [Cohen et al.1991] Cohen, F.R., Cohen, R.L., Mann, B.M., Milgram, R.J.: The topology of the space of rational functions and divisors of surfaces. Acta Math. 166, 163–221 (1991)
- [Gorinov2005] Gorinov, A.: Real cohomology groups of the space of nonsingular curves of degree 5 in ${\mathbb{CP}}^{2}$. Ann. Fac. Toulouse Math. (6) 14(3), 395–434 (2005).
- [Kallel and Karoui2011] Kallel, S., Karoui, R.: Symmetric joins and weighted barycenters. Adv. Nonlinear Stud. 11, 117–143 (2011).
- [Kozlowski and Yamaguchi2000] Kozlowski, A., Yamaguchi, R.: Topology of complements of discriminants and resultants. J. Math. Soc. Jpn. 52(4), 949–959 (2000)
- [Vassiliev1994] Vassiliev, V.A.: Complements of Discriminants of Smooth Maps: Topology and Applications. Revised edition, Translation in Mathematical Monographs, vol. 98. AMS, Providence (1994)
- [Vassiliev1997] Vassiliev, V.A.: Topology of Complements of Discriminants. Moscow, Phasis, p. 552 (1997) (in Russian)
- [Vassiliev1998] Vassiliev, V.A.: Homology of spaces of homogeneous polynomials in ${\mathbb{R}}^{2}$ without multiple zeros. Proc. Steklov Math. Inst. 221, 143–148 (1998).
- [Vassiliev1999] Vassiliev, V.A.: How to calculte the homology of spaces of nonsingular algebraic projective hypersurfaces. Proc. Steklov Math. Inst. 225, 121–140 (1999).