On Maps Taking Lines to Plane Curves
vtimorin@hotmail.com; vtimorin@hse.ru
Abstract
We study cubic rational maps that take lines to plane curves. A complete description of such cubic rational maps concludes the classification of all planarizations, i.e., maps taking lines to plane curves.
Keywords
Acknowledgements
1 Introduction
Let $\mathbb{P}^{n}$ be the projective space of dimension $n$ over $\mathbb{R}$ or $\mathbb{C}$. In [Timorin2012], a planarization was defined as a mapping $\Phi:U\to\mathbb{P}^{n}$, where $U\subset\mathbb{P}^{2}$ is an open subset, such that $\Phi(\lambda\cap U)$ is a subset of a hyperplane, for every line $\lambda\subset\mathbb{P}^{2}$. Studying planarizations is closely related to studying maps taking lines to curves of certain linear systems; a classical result of this type is the Möbius–von Staudt theorem ([Möbius1885]; [von Staudt1847]) about maps taking lines to lines, sometimes called the Fundamental Theorem of Projective Geometry. We will always assume that the planarizations are sufficiently smooth, i.e., sufficiently many times differentiable. If the ground field is $\mathbb{C}$, then we assume analyticity. The main result of this paper, stated below, is a complete description of all planarizations in case $n=3$.
Before stating the main result, we recall the motivation for studying planarizations ([Timorin2012]). An interesting class of problems consists of finding all transformations of a planar domain into a (in general) different planar domain that take line segments to arcs of curves in a given linear system $\mathcal{L}$. Say, if $\mathcal{L}$ is the linear system of all circles, then we are finding transformations taking lines to circles (including degenerations, i.e., straight lines). This particular problem was initially motivated by Nomography ([Khovanskii1976]), and it was solved in [Khovanskii1980]. Maps taking lines to circles have also been investigated in higher dimensions ([Izadi2005]; [Timorin2003]; [Timorin2004]). Large classes of such maps are provided by generalized Hopf fibrations ([Timorin2006]) and, more generally, by quadratic rational parameterizations of spheres ([Timorin2005]). Another motivation comes from freeform architecture, for which surfaces formed by simple planar curves are of special interest, see [Deng et al.2011].
We now state the problem more precisely. Let $\mathcal{L}$ be a linear system of algebraic curves in $\mathbb{P}^{2}$, and let $U\subset\mathbb{P}^{2}$ be an open set. We say that a map $f:U\to\mathbb{P}^{2}$ takes all lines to $\mathcal{L}$-curves if $f(U\cap L)$ is a subset of a curve from $\mathcal{L}$, for every line $L\subset\mathbb{P}^{2}$. For various linear systems $\mathcal{L}$, we would like to know all sufficiently smooth maps that take lines to $\mathcal{L}$-curves. If a sufficiently smooth map $f:U\to\mathbb{P}^{2}$ takes lines to $\mathcal{L}$-curves, then it gives rise to a planarization $F=\Phi_{\mathcal{L}}\circ f:U\dashrightarrow\mathbb{P}^{n}$, where $\Phi_{\mathcal{L}}:\mathbb{P}^{2}\dashrightarrow\mathbb{P}^{n}$ is the rational map, whose homogeneous components are generating equations for $\mathcal{L}$. This was the original motivation for studying planarizations. For example, to describe maps taking line segments to conics, we need to consider planarizations with values in $\mathbb{P}^{5}$.
Main Theorem.
Let $\Phi:U\to\mathbb{P}^{3}$ be a planarization. Then there is a nonempty open subset $V\subset U,$ for which the planarization $\Phi|_{V}:V\to\mathbb{P}^{3}$ is trivial$,$ or co-trivial$,$ or quadratic$,$ or dual quadratic.
We need to explain the terminology. A planarization $\Phi:V\to\mathbb{P}^{3}$ is said to be trivial if $\Phi(V)$ is a subset of a plane. A planarization $\Phi:V\to\mathbb{P}^{3}$ is said to be co-trivial if there exists a point $b\in\mathbb{P}^{3}$ such that, for every line $\lambda\subset\mathbb{P}^{2}$, the set $\Phi(\lambda\cap V)$ lies in a plane containing $b$. Of course, logically, co-trivial planarizations include trivial planarizations. On the other hand, there are “more” trivial planarizations than co-trivial planarizations that are not trivial. This is one of the reasons for distinguishing trivial planarizations as a separate class; the second reason being a partial duality between trivial and co-trivial planarizations. Trivial planarizations can be described in terms of an arbitrary map from $\mathbb{P}^{2}$ to $\mathbb{P}^{2}$, and co-trivial planarizations can be described in terms of an arbitrary function on $\mathbb{P}^{2}$ (see Theorem 6.1).
A map $\Phi:V\to\mathbb{P}^{3}$ is said to be a quadratic rational map if in some (hence any) system of homogeneous coordinates it is given by quadratic homogeneous polynomials. In other words, there are quadratic homogeneous polynomials $Q_{0}$, $Q_{1}$, $Q_{2}$ and $Q_{3}$ in $x_{0}$, $x_{1}$, $x_{2}$ such that $\Phi$ maps a point with homogeneous coordinates $[x_{0}:x_{1}:x_{2}]$ to the point with homogeneous coordinates $[y_{0}:y_{1}:y_{2}:y_{3}]$, where
| $\displaystyle y_{\alpha}=Q_{\alpha}(x_{0},x_{1},x_{2}),\quad\alpha=0,1,2,3.$ |
It is easy to see that every quadratic rational map takes lines to conics, in particular, every quadratic rational map is a planarization. Some quadratic planarizations are neither trivial nor co-trivial.
Another class of examples is provided by duality. Let $\Phi:V\to\mathbb{P}^{3}$ be a planarization. Recall that the dual projective plane $\mathbb{P}^{2*}$ consists of lines in $\mathbb{P}^{2}$, and the dual projective space $\mathbb{P}^{3*}$ consists of planes in $\mathbb{P}^{3}$. Let $V^{*}$ be the subset of $\mathbb{P}^{2*}$ consisting of all lines $\lambda\subset\mathbb{P}^{2}$ with the following property: the set $\Phi(\lambda\cap V)$ lies in a unique plane $P_{\lambda}$. Note that the set $V^{*}$ is open, possibly empty. The dual planarization $\Phi^{*}:V^{*}\to\mathbb{P}^{3*}$ is by definition the map taking $\lambda$ to $P_{\lambda}$. Given a coordinate representation of $\Phi$, it is easy to write explicit formulas for $\Phi^{*}$. It turns out that a planarization dual to a quadratic rational map is a special kind of cubic rational map. Such planarization is called dual quadratic. It is rather obvious that the duality is symmetric: if $\Phi:V\to\mathbb{P}^{3}$ is a planarization, $\Phi^{*}:V^{*}\to\mathbb{P}^{3*}$ is the dual planarization with a nonempty domain $V^{*}$, and $V^{**}\cap V\neq\varnothing$, then $\Phi=\Phi^{**}$ on $V^{**}\cap V$.
It is proved in [Timorin2012] that a planarization $\Phi:U\to\mathbb{P}^{3}$ that is neither trivial nor co-trivial must be a rational map of degree two or three, at least on some nonempty open subset of $U$. Thus, to prove the Main Theorem, it suffices to describe all cubic planarizations. A cubic planarization is defined globally as a rational map from $\mathbb{P}^{2}$ to $\mathbb{P}^{3}$ (it may have some points of indeterminacy). Moreover, it suffices to assume that the ground field is $\mathbb{C}$.
It is natural to consider the following equivalence relation on the set of all planarizations. Given two planarizations $\Phi:V\to\mathbb{P}^{3}$, $\Phi^{\prime}:V^{\prime}\to\mathbb{P}^{3}$ we say that they are equivalent if they coincide on some nonempty open set after suitable projective coordinate changes in $\mathbb{P}^{2}$ and in $\mathbb{P}^{3}$. In other terms, there are projective automorphisms $\eta\in\mathrm{PGL}_{2}$, $\mu\in\mathrm{PGL}_{3}$, and a nonempty open subset $W\subset V\cap\eta^{-1}(V^{\prime})$ such that $\Phi=\mu\circ\Phi^{\prime}\circ\eta$ on $W$. In Sect. 6, we describe all equivalence classes of planarizations over real numbers by specifying a representative in each class. These representatives will also be called normal forms of planarizations, so that every planarization is projectively equivalent to some normal form. Of course, there are infinitely many classes of trivial and co-trivial planarizations. These classes can be described by means of function parameters, i.e., they depend on some arbitrary functions. Other than that, there are 16 classes. Our classification is based on the classification of equivalence classes of quadratic rational maps ([Coffman et al.1996]).
Studying planarizations for $n>3$ is also important, e.g., the case $n=5$ relates to studying maps that take lines to conics. As in the case $n=3$, we expect that, apart from (co-)trivial cases, planarizations must be rational maps of low degree. An explicit upper bound for the degree is easy to conjecture: $\frac{n(n-1)}{2}$. On the other hand, we do not know even a conjectural description of all planarizations for $n>3$.
Organization of the paper In Sect. 2, we recall some basic properties of cubic rational maps and the associated linear webs of plane cubic curves. In Sect. 3, we address specific properties of cubic planarizations. The main result of this section is that a cubic planarization that is neither trivial nor co-trivial and that has only finitely many points of indeterminacy must map $\mathbb{P}^{2}$ many-to-one to its image surface. In Sect. 4, we complete the description of all cubic planarizations thus proving the Main Theorem. Section 5 is a digression needed for a classification of all planarizations up to equivalence. In this section, we classify all quadratic planarizations. Finally, in Sect. 6, we give a list of normal forms for planarizations.
2 Cubic Maps and Base Points
Let us introduce some notation and conventions that will be used throughout the paper. First, all spaces and maps are defined over complex numbers. Let $\Phi:\mathbb{P}^{2}\dashrightarrow\mathbb{P}^{3}$ be a cubic rational map sending a point of $\mathbb{P}^{2}$ with homogeneous coordinates $[x_{0}:x_{1}:x_{2}]$ to a point of $\mathbb{P}^{3}$ with homogeneous coordinates $[y_{0}:y_{1}:y_{2}:y_{3}]$, where
| $\displaystyle y_{\alpha}=\varphi_{\alpha}(x_{0},x_{1},x_{2}),\quad\alpha=0,1,2 ,3,$ |
and $\varphi_{\alpha}$ is a homogeneous polynomial in three variables of degree 3. Recall that an indeterminacy point of $\Phi$ is a point $x$ in $\mathbb{P}^{2}$ such that $\varphi_{\alpha}(x)=0$ for all $\alpha=0$, 1, 2, 3. This is precisely a point that does not have an image under $\Phi$.
Recall that $\Phi$ defines a linear system $\mathcal{L}_{\Phi}$ of plane cubics of dimension 3 (a three-dimensional linear system is called a linear web). By definition, $\mathcal{L}_{\Phi}$ is generated by the cubics $\varphi_{\alpha}=0$, i.e., the equation of any cubic in $\mathcal{L}_{\Phi}$ has the form
| $\displaystyle c_{0}\varphi_{0}+c_{1}\varphi_{1}+c_{2}\varphi_{2}+c_{3}\varphi_ {3}=0,$ |
where the coefficients $c_{0}$, $c_{1}$, $c_{2}$, $c_{3}$ are complex numbers not vanishing simultaneously, thus $[c_{0}:c_{1}:c_{2}:c_{3}]$ can be thought of as a point in $\mathbb{P}^{3}$, or, in more invariant terms, as a point in the dual projective space $\mathbb{P}^{3*}$ defining a plane $P$ in $\mathbb{P}^{3}$. Indeterminacy points of $\Phi$ are also called the base points of $\mathcal{L}_{\Phi}$. We will write $B_{\Phi}$ for the set of all base points of $\mathcal{L}_{\Phi}$. Every cubic from $\mathcal{L}_{\Phi}$ contains the set $B_{\Phi}$. To each plane $P$ in $\mathbb{P}^{3}$, we may associate the set $\varkappa_{P}=B_{\Phi}\cup\Phi^{-1}(P)$ in $\mathbb{P}^{2}$; clearly, if $\varphi_{0},\ldots,\varphi_{3}$ are linearly independent, then $\varkappa_{P}$ is a plane cubic curve, possibly degenerate.
Lemma 2.1.
If $B_{\Phi}$ contains an irreducible curve $\beta,$ then this curve has degree at most three. Moreover$,$ the restriction of $\Phi$ to the complement $\mathbb{P}^{2}{\setminus}\beta$ coincides with a rational map of degree less than 3.
Proof.
Let $\xi=0$ be an irreducible equation defining the curve $\beta$. Note that the components of $\Phi$ are divisible by $\xi$. Therefore, the restriction of $\Phi$ to the complement of $\beta$ coincides with the rational map $\xi^{-1}\Phi$ of degree $3-\deg(\beta)$. $\square$
For this reason, we will mostly assume that $B_{\Phi}$ is a finite set of points. There is a natural way of assigning multiplicity to every point $b\in B_{\Phi}$. Namely, the multiplicity $m(b)$ is equal to the minimum intersection index of two cubics in $\mathcal{L}_{\Phi}$ at $b$. Since all cubics in $\mathcal{L}_{\Phi}$ pass through $b$, we have $m(b)\geq 1$. We will write $|B_{\Phi}|$ for the number of points in $B_{\Phi}$ counting multiplicities. In other terms, we have by definition
| $\displaystyle|B_{\Phi}|=\sum_{b\in B_{\Phi}}m(b).$ |
We will write $S_{\Phi}=\Phi(\mathbb{P}^{2}{\setminus}B_{\Phi})$ for the image of $\Phi$ and $\overline{S}_{\Phi}$ for its projective closure in $\mathbb{P}^{3}$. Note that if $\Phi$ is a planarization and dimension of $S_{\Phi}$ is one, then $S_{\Phi}$ is a planar curve, hence $\Phi$ is trivial. Thus, the case when $S_{\Phi}$ is a curve is not interesting.
In what follows, we recall how to define the topological degree of the map $\Phi$. Suppose that $B_{\Phi}$ is finite and that $S_{\Phi}$ has dimension two. By [Beauville1996], Theorem II.7 (elimination of indeterminacy), there exists a smooth compact projective surface $X$, a regular morphism $\pi:X\to\mathbb{P}^{2}$ that is a finite composition of blow-ups, and a regular morphism $\Psi:X\to\mathbb{P}^{3}$ with the property $\Psi=\Phi\circ\pi$, which holds where the right-hand side is defined. By the Specialization Principle, cf. [Mumford1976], Theorem (3.25), and since the dimension of $\Psi(X)\supset S_{\Phi}$ is 2, a generic point in $\Psi(X)$ has exactly $k$ preimages in $X$, where $k$ is the degree of the field extension $\mathbb{C}(X)/\Psi^{*}\mathbb{C}(\Psi(X))$. The difference $X{\setminus}\pi^{-1}(\mathbb{P}^{2}{\setminus}B_{\Phi})$ consists of exceptional curves, whose images under $\Psi$ lie in a proper Zariski closed subset of $\Psi(X)$. Therefore, a generic point of $S_{\Phi}$ has exactly $k$ preimages in $\mathbb{P}^{2}{\setminus}B_{\Phi}$. We will call the number $k$ the topological degree of $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$.
The following proposition is classical and well known but we recall the proof for completeness.
Proposition 2.2.
Suppose that $|B_{\Phi}|<\infty$ and $\dim(S_{\Phi})=2$. Let $k$ be the topological degree of $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$. Then the projective closure of $S_{\Phi}$ is a surface of degree $(9-|B_{\Phi}|)/k,$ in particular$,$ $|B_{\Phi}|<9$.
Proof.
Let $d$ denote the degree of the surface $\overline{S}_{\Phi}$. By the Kleiman transversality theorem, there is a proper Zariski closed set $\mathcal{Z}_{1}$ of lines in $\mathbb{P}^{3}$ such that every line $L\not\in\mathcal{Z}_{1}$ intersects the set $S_{\Phi}$ transversely at exactly $d$ points. There is some at most one-dimensional exceptional subvariety $E$ of $S_{\Phi}$ such that all points outside of $E$ have exactly $k$ preimages under $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$. There is a proper Zariski closed set $\mathcal{Z}_{2}$ of lines in $\mathbb{P}^{3}$ containing all lines intersecting $E$. Every line $L\subset\mathbb{P}^{3}$ defines a pencil $\mathcal{L}_{\Phi}(L)\subset\mathcal{L}_{\Phi}$ consisting of all cubics $\varkappa_{P}$, where $P$ runs through all planes containing $L$. Let $\nu(L)$ be the sum of intersection indices of two generic curves in $\mathcal{L}_{\Phi}(L)$ at points of $B_{\Phi}$. Clearly, there is a proper Zariski closed set $\mathcal{Z}_{3}$ of lines containing all lines $L$ with $\nu(L)\neq|B_{\Phi}|$.
Consider a line $L$ not in $\mathcal{Z}_{1}\cup\mathcal{Z}_{2}\cup\mathcal{Z}_{3}$. Then the set $S_{\Phi}\cap L$ consists of $d$ transverse intersection points. The line $L$ can be represented as the intersection of two planes $P_{1}$ and $P_{2}$. Note that the curves $P_{1}\cap S_{\Phi}$ and $P_{2}\cap S_{\Phi}$ intersect transversely, since all intersection points of $L=P_{1}\cap P_{2}$ and $S_{\Phi}$ are transverse. Let $\varkappa_{1}$ and $\varkappa_{2}$ be the corresponding cubics in $\mathcal{L}_{\Phi}$. Since $L\not\in\mathcal{Z}_{1}\cup\mathcal{Z}_{2}$, the intersection $\varkappa_{1}\cap\varkappa_{2}$ is a disjoint union of $dk$ intersection points and the set $B_{\Phi}$. At each of these $dk$ points, the intersection is transverse since $\Phi$ is locally a diffeomorphic embedding, and the images of $\varkappa_{1}$, $\varkappa_{2}$ intersect transversely. Since $L\not\in\mathcal{Z}_{3}$, the sum of intersection indices of $\varkappa_{1}$ and $\varkappa_{2}$ at points of $B_{\Phi}$ is equal to $|B_{\Phi}|$. By the Bezout theorem, we have $9=3^{2}=dk+|B_{\Phi}|$. $\square$
3 Planarizations
As before, we consider a cubic rational map $\Phi$. We now assume that $\Phi$ is a planarization, i.e., the $\Phi$-image of every line in $\mathbb{P}^{2}$ is a subset of some plane in $\mathbb{P}^{3}$. We say that $\Phi$ is strictly cubic if there is no Zariski open subset $U\subset\mathbb{P}^{2}$ such that the restriction of $\Phi$ to $U$ coincides with some quadratic rational map. It follows from Lemma 2.1 that for every strictly cubic planarization $\Phi$, the set $B_{\Phi}$ is finite.
The next proposition is needed to formulate the theorem we will prove in this section.
Proposition 3.1.
Suppose that $\Phi:\mathbb{P}^{2}\dashrightarrow\mathbb{P}^{3}$ is a strictly cubic planarization that is not co-trivial. Then the dimension of $S_{\Phi}$ is two.
To prove this proposition we need the following lemma.
Lemma 3.2.
Suppose that $\Phi$ is not co-trivial. Then all fibers of $\Phi$ are finite$,$ i.e.$,$ there is no semi-algebraic subset of dimension one in $\mathbb{P}^{2}$ mapping to a point.
Proof.
Suppose that $\Gamma\subset\mathbb{P}^{2}{\setminus}B_{\Phi}$ is a semi-algebraic subset of dimension one such that $\Phi(\Gamma)$ is a point. Note that a generic line $\lambda\subset\mathbb{P}^{2}$ intersects $\Gamma$. Therefore, the plane $P_{\lambda}$ passes through the point $\Phi(\Gamma)$. It follows that $\Phi$ is co-trivial. $\square$
Proof of Proposition 3.1.
Suppose that on the contrary $S_{\Phi}$ has dimension one. Then by the inverse function theorem and Sard’s lemma there is $x\in S_{\Phi}$ such that $\Phi^{-1}(x)$ in $\mathbb{P}^{2}$ is semi-algebraic set of dimension one, contradiction to the Lemma 3.2. $\square$
The following theorem is proved in this section.
Theorem 3.3.
Suppose that $\Phi:\mathbb{P}^{2}\dashrightarrow\mathbb{P}^{3}$ is a strictly cubic planarization$,$ which is not co-trivial. Then the topological degree of $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ is greater than one.
Note that, under the assumptions of Theorem 3.3, the topological degree of $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ is well defined by Proposition 3.1.
First, we examine general properties of strictly cubic planarizations that are needed to prove Theorem 3.3.
Lemma 3.4.
Suppose that $\Phi$ is a strictly cubic planarization. For a generic choice of line $\lambda$ in $\mathbb{P}^{2},$ the curve $\Phi(\lambda)$ is cubic.
Proof.
Suppose that the degree of $\Phi(\lambda)$ is at most 2, for a Zariski open set of lines $\lambda$. Then, by [Timorin2012], Lemma 2.8, the map $\Phi$ is not strictly cubic, a contradiction. $\square$
We will write $J_{\Phi}$ for the semi-algebraic set in $\mathbb{P}^{2}$, on which the Jacobian of $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ vanishes. In other terms, $J_{\Phi}$ consists of all points $p\in\mathbb{P}^{2}$ such that the differential $d_{p}\Phi$ of $\Phi$ at $p$ is degenerate, i.e., has a nontrivial kernel. Note that if $\Phi$ is strictly cubic and not co-trivial, then, by Proposition 3.1, $S_{\Phi}$ has dimension two. Then, by the Sard lemma, the Jacobian of $\Phi$ cannot vanish everywhere. Therefore, the dimension of $J_{\Phi}$ is at most one.
Proposition 3.5.
Suppose that $\Phi$ is not co-trivial and $\dim(J_{\Phi})=1$. Then every component of $J_{\Phi}$ of dimension one is mapped to a subset of a plane.
To prove Proposition 3.5, we need the following simple and general lemma:
Lemma 3.6.
If a germ of a holomorphic curve $T\subset\mathbb{P}^{3}$ has the property that all tangent lines of $T$ pass through some point $b\in\mathbb{P}^{3},$ then in fact $T$ lies in a line passing through $b$.
Proof.
We may choose homogeneous coordinates in $\mathbb{P}^{3}$ so that $b=[0:0:0:1]$. In the affine chart $(x_{1},x_{2},x_{3})\mapsto[1:x_{1}:x_{2}:x_{3}]$, the lines passing through $b$ are tangent to the vertical line field. The only integral curves of the vertical line field are vertical lines. $\square$
Proof of Proposition 3.5.
Let $K$ be a component of $J_{\Phi}$, whose dimension is one. The set $\Phi(K)$ is not a point, by Lemma 3.2. Since $K$ is not mapped to a point under $\Phi$, the restriction of $\Phi$ to $K$ has only finitely many critical points. Note that, if $K$ lies in a line, then the statement follows from the definition of a planarization. Thus, we may assume that $K$ is not a subset of a line.
We now define three proper Zariski closed subsets $\mathcal{Z}_{1}$, $\mathcal{Z}_{2}$ and $\mathcal{Z}_{3}$ of $K\times K$. The set $\mathcal{Z}_{1}$ is defined as the set of pairs $(p,q)\in K\times K$ such that $p$ or $q$ is a critical point of $\Phi|_{K}$. Since $\Phi|_{K}$ has finitely many critical points, $\mathcal{Z}_{1}$ is a proper Zariski closed subset of $K\times K$. The set $\mathcal{Z}_{2}$ is by definition the closure of the set of pairs $(p,q)\in K\times K$ with $p\neq q$ such that the line connecting $p$ and $q$ is non-special, i.e., the image of this line is not a subset of a line. This set is closed by definition. Since a generic line is non-special (by the Möbius–von Staudt theorem), the set $\mathcal{Z}_{2}$ is proper. Finally, we define the set $\mathcal{Z}_{3}$ as the closure of the set of pairs $(p,q)\in K\times K$ with the following properties: there is a unique line $\lambda$ connecting $p$ and $q$; the restriction of the differential $d_{p}\Phi$ to the tangent line of $\lambda$ at $p$ vanishes or the restriction of the differential $d_{q}\Phi$ to the tangent line of $\lambda$ at $q$ vanishes. By definition, $\mathcal{Z}_{3}$ is closed. Since the restriction of $\Phi$ to a generic line has finitely many critical points, the set $\mathcal{Z}_{3}$ is proper.
We now assume that $(p,q)$ does not belong to $\mathcal{Z}_{1}\cup\mathcal{Z}_{2}\cup\mathcal{Z}_{3}$. Since $p$, $q\in J_{\Phi}$, the curve $\Phi(K)$ is tangent to $\Phi(\lambda)$ at points $\Phi(p)$ and $\Phi(q)$. Moreover, since $(p,q)\not\in\mathcal{Z}_{1}\cup\mathcal{Z}_{3}$, the point $\Phi(p)$ is nonsingular for $\Phi(K\cap U_{p})$ and $\Phi(\lambda\cap U_{p})$, where $U_{p}$ is a small neighborhood of $p$, and the point $\Phi(q)$ is nonsingular for $\Phi(K\cap U_{q})$ and $\Phi(\lambda\cap U_{q})$, where $U_{q}$ is a small neighborhood of $q$. Therefore, the submanifolds $\Phi(K\cap U_{p})$, $\Phi(\lambda\cap U_{p})$ have well-defined tangent lines at $\Phi(p)$, and similarly for $q$.
It follows that the curve $\Phi(K)$ is tangent to the plane $P_{\lambda}$ at $\Phi(p)$ and $\Phi(q)$. Tangent lines of $\Phi(K)$ at $\Phi(p)$ and $\Phi(q)$ lie in the same plane $P_{\lambda}$, hence they intersect. Since this is true for a Zariski dense set of pairs $(p,q)$, it follows that every pair of tangent lines of $\Phi(K)$ intersect. Fix two tangent lines $\Lambda_{1}$ and $\Lambda_{2}$ of $\Phi(K)$. Any other tangent line $\Lambda$ of $\Phi(K)$ must intersect both $\Lambda_{1}$ and $\Lambda_{2}$. Thus, either $\Lambda$ lies in the plane containing $\Lambda_{1}\cup\Lambda_{2}$, or $\Lambda$ passes through the intersection point $\Lambda_{1}\cap\Lambda_{2}$. We see that the only possibilities for $\Phi(K)$ are that
-
1.
all tangent lines of this curve lie in the same plane, OR
-
2.
all tangent lines of this curve pass through the same point.
In case (2), we have that $\Phi(K)$ is a subset of some line by Lemma 3.6, therefore, $\Phi(K)$ is a subset of a plane. In case (1), we have that all tangent lines of $\Phi(K)$ belong to the same plane, therefore, the curve $\Phi(K)$ itself lies in this plane. $\square$
Corollary 3.7.
Suppose that $\Phi$ is not co-trivial and $K$ is one-dimensional component of $J_{\Phi}$ that is not contained in any line. Then the $\Phi$-image of a generic line $\lambda\subset\mathbb{P}^{2}$ is tangent to $\Phi(K)$ at two or more points.
Proof.
By the assumption, the curve $K$ has degree at least two. Hence, a generic line $\lambda\subset\mathbb{P}^{2}$ intersects $K$ at two different points $p$, $q$ with a property $\Phi(p)\neq\Phi(q)$. Thus, $\Phi(\lambda)$ is tangent to $\Phi(K)$ at $\Phi(p),\Phi(q)$. $\square$
Proposition 3.8.
Suppose that $\Phi$ is strictly cubic$,$ not co-trivial$,$ and not dual quadratic. Suppose also that the topological degree of $\Phi$ is equal to one. Then the set $J_{\Phi}$ is finite$,$ possibly empty.
To prove this proposition, we need the following lemma:
Lemma 3.9.
Suppose that $\Phi$ is strictly cubic$,$ the topological degree of $\Phi$ is one$,$ and $S_{\Phi}$ is a two-dimensional subset of some surface of degree 2 or 3. Then $\Phi$ is trivial or co-trivial.
We need to introduce some terminology. A line $\lambda\subset\mathbb{P}^{2}$ is called non-special for a planarization $\Phi$ if $\Phi(\lambda)$ is not a line. By the Möbius–von Staudt theorem and since $\Phi$ is strictly cubic, a generic line in $\mathbb{P}^{2}$ is non-special for $\Phi$. Since $\Phi$ is a planarization, for every non-special line $\lambda$, there is a unique plane $P_{\lambda}$ in $\mathbb{P}^{3}$ containing $\Phi(\lambda)$. If $\Phi$ is cubic and not (co)-trivial, then the preimage $\Phi^{-1}(P_{\lambda})$ lies in a unique cubic curve $\varkappa_{\lambda}\in\mathcal{L}_{\Phi}$ containing $\lambda$. In fact, $\Phi^{-1}(P_{\lambda})$ coincides with $\varkappa_{\lambda}{\setminus}B_{\Phi}$. Then $\varkappa_{\lambda}=\lambda\cup\sigma_{\lambda}$, where $\sigma_{\lambda}$ is a conic. The curves $\Phi(\lambda)$ and $\Phi(\sigma_{\lambda})$ are two plane curves in $\mathbb{P}^{3}$.
Proof of Lemma 3.9.
Suppose that $S_{\Phi}$ is a two-dimensional subset of some surface of degree 3. By Proposition 2.2, we have $|B_{\Phi}|=6$. Suppose that $\Phi$ is not co-trivial, then for every non-special line $\lambda\subset\mathbb{P}^{2}$ disjoint from $B_{\Phi}$, consider the corresponding conic $\sigma_{\lambda}$. Then $\sigma_{\lambda}$ contains the set $B_{\Phi}$. Moreover, we have $(\sigma_{\lambda}\cdot\varkappa)_{B_{\Phi}}\geq 6$, where $\varkappa$ is any cubic from the linear web $\mathcal{L}_{\Phi}$, and $(\sigma_{\lambda}\cdot\varkappa)_{B_{\Phi}}$ denotes the sum of the intersection multiplicities of $\sigma_{\lambda}$ and $\varkappa$ at all points of $B_{\Phi}$. Indeed, if $\lambda\cap B_{\Phi}=\varnothing$, then the inequality $(\sigma_{\lambda}\cdot\varkappa)_{B_{\Phi}}\geq 6$ follows from $((\sigma_{\lambda}+\lambda)\cdot\varkappa)_{B_{\Phi}}\geq 6$. The latter inequality holds by definition of $|B_{\Phi}|$: any pair of cubics from the linear system $\mathcal{L}_{\Phi}$ intersects at $|B_{\Phi}|$ or more points of $B_{\Phi}$, counting multiplicities. The case when $\lambda\cap B_{\Phi}\neq\varnothing$ follows from the upper-semicontinuity of the intersection multiplicities.
If a line $\lambda^{\prime}$ is disjoint from $B_{\Phi}$, then $(\sigma_{\lambda}\cdot\sigma_{\lambda^{\prime}})_{B_{\Phi}}=(\sigma_{\lambda} \cdot\varkappa_{\lambda^{\prime}})_{B_{\Phi}}\geq 6$. On the other hand, two different conics either share a line component or intersect by at most 4 points, counting multiplicities. It follows that all conics $\sigma_{\lambda}$ share a line component $\lambda_{0}$, in particular, all $\sigma_{\lambda}$ have a point $a\notin B_{\Phi}$ in common. Then, for every line $\lambda\subset\mathbb{P}^{2}$, the plane $P_{\lambda}$ containing the image of $\lambda$ contains also $\Phi(a)$, which means that $\Phi$ must be co-trivial.
The same proof by contradiction works for the case of degree 2. $\square$
Proof of Proposition 3.8.
Assume the contrary: there is a component $K$ of $J_{\Phi}$ that has dimension one. By Proposition 3.5, the image $\Phi(K)$ is a plane curve. Consider the following cases.
First, suppose that neither $K$ nor $\Phi(K)$ is a subset of a line. We will write $P$ for the plane containing $\Phi(K)$. By the Corollary 3.7, the image of a generic line $\lambda\subset\mathbb{P}^{2}$ under the map $\Phi$ is tangent to $\Phi(K)$ at two or more points. Moreover, we may assume that the tangent lines of $\Phi(K)$ at these points do not coincide and therefore define a unique plane. It follows that $P_{\lambda}=P$. Since $\lambda$ is generic, this implies that $\Phi$ is trivial and hence co-trivial, a contradiction.
Second, suppose now that $\Phi(K)$ lies in a line $L\subset\mathbb{P}^{3}$. Then, since, for a generic line $\lambda\subset\mathbb{P}^{2}$, the curve $\Phi(\lambda)$ is tangent to $\Phi(K)$, the plane $P_{\lambda}$ must contain $L$. It follows that $\Phi$ is co-trivial, a contradiction.
Finally, suppose that $K$ is a subset of a line but $\Phi(K)$ is not a subset of a line. Then $\Phi(K)$ lies in a plane algebraic curve $\Xi$ of degree two or three. Consider the dual planarization $\Phi^{*}$. If $\Phi$ is strictly cubic, then $\Phi^{*}$ is defined on some nonempty Zariski open subset of $\mathbb{P}^{2*}$. If $\Phi^{*}$ is trivial, then $\Phi$ must be co-trivial. If $\Phi^{*}$ is co-trivial, then $\Phi$ must be trivial. Thus we may assume that $\Phi^{*}$ is neither trivial nor co-trivial. Note that, for a generic line $\lambda\subset\mathbb{P}^{2}$, the image $\Phi(\lambda)$ is tangent to $\Phi(K)$ at the point $\Phi(\lambda\cap K)$. It follows that the plane $P_{\lambda}$ is tangent to $\Phi(K)$. We see that the image $\Phi^{*}(\mathbb{P}^{2*}{\setminus}B_{\Phi^{*}})$ lies in the set of all tangent planes of $\Xi$.
The set $\Xi^{*}$ of all tangent planes of $\Xi$ is a cone in $\mathbb{P}^{3*}$ (indeed, every plane in $\Xi^{*}$ is an element of a linear pencil of planes, i.e., of a line in $\mathbb{P}^{3*}$, containing the plane of $\Xi$). A plane section of the cone $\Xi^{*}$ not passing through the vertex of this cone is a curve projectively equivalent to the dual curve of $\Xi$. Since $\Phi^{*}$ is a planarization that is neither co-trivial nor dual quadratic, it must be a strictly cubic planarization by [Timorin2012], Theorem 1.1. It follows that the projectively dual curve of $\Xi$ has degree at most three. Indeed, the image of a line under a cubic rational map lies in a curve of degree at most three. Then the degree of the surface $\Xi^{*}$ is also at most three. By Proposition 3.1, we may assume that $\Phi^{*}(\mathbb{P}^{2*}{\setminus}B_{\Phi^{*}})$ has dimension two, i.e., includes an open subset of $\Xi^{*}$. It now follows from Lemma 3.9 that the planarization $\Phi$ is trivial or co-trivial, a contradiction. $\square$
By Lemma 3.4, if $\Phi$ is a strictly cubic planarization then the image $\Phi(\lambda)$ of a generic line $\lambda\subset\mathbb{P}^{2}$, is a cubic curve. We need the following proposition.
Proposition 3.10.
Suppose $\Phi$ is strictly cubic, not co-trivial and not dual quadratic. Assume also that the topological degree of $\Phi$ is one. Then the set of all lines $\lambda\subset\mathbb{P}^{2},$ such that their $\Phi$-images are cuspidal cubics$,$ is not Zariski dense.
Proof.
We will write $\gamma$ for the Zariski closure of the set of all points $p$ with the following property: there is a line $\lambda\ni p$, whose $\Phi$-image is a cuspidal cubic curve, the point $\Phi(p)$ being the cusp of this curve. If $p$ and $\lambda$ are as above, then $p\in J_{\Phi}$. It follows that $\gamma\subset J_{\Phi}$ has dimension at most one. Since a generic line intersects $\gamma$, we conclude that $\gamma$ is a curve rather than a finite set of points. But this contradicts the results of Proposition 3.8, which states that $J_{\Phi}$ and hence $\gamma$ are finite sets. $\square$
A plane rational cubic curve is either nodal or cuspidal. Let $\Omega_{\Phi}$ denote the set of lines $\lambda\subset\mathbb{P}^{2}$, such that the cubic $\Phi(\lambda)$ is nodal. For every line $\lambda\in\Omega_{\Phi}$, we let $\Sigma(\lambda)$ be the set of points of $\lambda$ mapping to the singular point of the unique nodal cubic curve containing $\Phi(\lambda)$. Thus the set $\Sigma(\lambda)$ consists of pairs of points such that each pair is mapped to the node of the unique nodal cubic containing $\Phi(\lambda)$. Let $\Gamma_{\Phi}$ be the Zariski closure of the union of $\Sigma(\lambda)$ over all lines $\lambda\in\Omega_{\Phi}$.
Lemma 3.11.
Suppose that $\Phi$ is a non co-trivial planarization such that the set $\Omega_{\Phi}$ is non-empty and Zariski open. Then the set $\Gamma_{\Phi}$ coincides with the whole of $\mathbb{P}^{2}$ and the topological degree of $\Phi$ is greater than one.
Proof.
Assume the contrary: the set $\Gamma_{\Phi}$ has dimension one or less. Then the set $\mathcal{Z}$ of lines $\lambda$ such that $\Phi:\lambda\cap\Gamma_{\Phi}\to\mathbb{P}^{3}$ is not injective has dimension at most one. Indeed, given a point $a\in\Gamma_{\Phi}$, there are only finitely many lines connecting $a$ with some other point in the finite set $\Phi^{-1}(\Phi(a))$ (the latter set is finite by Lemma 3.2). Consider a line $\lambda\not\in\mathcal{Z}$. Moreover, we may assume that $\Phi(\lambda)$ is a nodal cubic and $\lambda\cap B_{\Phi}=\varnothing$. Then the set $\Sigma(\lambda)$ contains some point $b\neq a$. This is a contradiction with the fact that $\Phi$ is injective on the set $\lambda\cap\Gamma_{\Phi}$. Thus, the set $\Gamma_{\Phi}$ coincides with the whole of $\mathbb{P}^{2}$. In turn, this means that a generic point of $S_{\Phi}$ is a node of some nodal cubic lying on $S_{\Phi}$. Hence, the topological degree of $\Phi$ is greater than one. $\square$
We are now ready to give the proof of Theorem 3.3.
Proof of Theorem 3.3.
First, suppose $\Phi$ is a dual quadratic planarization satisfying all the assumptions of Theorem 3.3. Then we prove that the topological degree of $\Phi$ is greater than one, i.e. in this case the conclusion of Theorem 3.3 holds.
Indeed, let $\Phi^{*}$ be the dual planarization of $\Phi$. It is defined on some nonempty Zariski open subset of $\mathbb{P}^{2*}$. Since $\Phi$ is dual quadratic, the map $\Phi^{*}$ is a quadratic rational map. Recall that lines in $\mathbb{P}^{2*}$ correspond to points in $\mathbb{P}^{2}$: namely, a point $a\in\mathbb{P}^{2}$ defines the line $a^{*}\in\mathbb{P}^{2*}$ consisting of all lines in $\mathbb{P}^{2}$ passing through $a$. If a line $a^{*}\subset\mathbb{P}^{2*}$ is non-special for $\Phi^{*}$, we will write $P^{*}_{a}$ for the plane in $\mathbb{P}^{3*}$ containing the set $\Phi^{*}(a^{*}{\setminus}B_{\Phi^{*}})$. The plane $P^{*}_{a}$, of course, identifies with the point $\Phi^{**}(a)=\Phi(a)$. Taking a $\Phi^{*}$-preimage of the plane $P^{*}_{a}$ in $\mathbb{P}^{3*}$ defines a conic in $\mathbb{P}^{2*}$ containing $a^{*}$. This conic consists of $a^{*}$ and another line $a_{1}^{*}$. Clearly, we have $a_{1}\neq a$ for a generic $a\in\mathbb{P}^{2}$ (there is no nontrivial linear systems of double lines in $\mathbb{P}^{2}$) and that $\Phi(a_{1})=\Phi(a)$. It follows that the topological degree of $\Phi$ is greater than one.
The remaining part is proved by contradiction based on the above results. Namely, let $\Phi$ be a strictly cubic planarization that is not co-trivial and not dual quadratic. Assume that the topological degree of $\Phi$ equals one. By Proposition 3.10, we know that, for a generic line $\lambda$, the cubic $\Phi(\lambda)$ is not cuspidal. Therefore, the set $\Omega_{\Phi}$ is non-empty and Zariski open. Now, it follows from Lemma 3.11 that the topological degree of the map $\Phi$ is strictly greater than one, a contradiction. This concludes the proof of Theorem 3.3. $\square$
4 Description of Cubic Planarizations
In this section, we give a complete description of cubic planarizations thus completing the description of all planarizations. We will assume throughout this section that $\Phi$ is a strictly cubic planarization that is neither trivial nor co-trivial. Then $S_{\Phi}$ has dimension two, and the set $B_{\Phi}$ is finite. By Theorem 3.3, the topological degree of the map $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ is at least two. We can now make this result stronger.
Proposition 4.1.
If $\Phi$ is not dual quadratic$,$ then the topological degree of the map $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ is equal to three.
Proof.
Consider the dual planarization $\Phi^{*}$. Recall that it is defined on some nonempty Zariski open subset of $\mathbb{P}^{2*}$. By the [Timorin2012], Theorem 1.1, the map $\Phi^{*}$ must be cubic. Moreover, $\Phi^{*}$ is neither trivial, nor co-trivial (otherwise $\Phi$ would be trivial or co-trivial).
Consider the set $B_{\Phi^{*}}\subset\mathbb{P}^{2*}$ of all indeterminacy points of $\Phi^{*}$. Since $\Phi$ is not dual quadratic, the planarization $\Phi^{*}$ is strictly cubic. It follows by Lemma 2.1 that the set $B_{\Phi^{*}}$ is finite.
All facts established earlier for $\Phi$ apply also to $\Phi^{*}$. In particular, a generic fiber of the map $\Phi^{*}$ consists of at least two points by Theorem 3.3, and a generic line $a^{*}\subset\mathbb{P}^{2*}$ is mapped to a cubic under $\Phi^{*}$ by Lemma 3.4. If a line $a^{*}\subset\mathbb{P}^{2*}$ is non-special for $\Phi^{*}$, then we will write $P^{*}_{a^{*}}$ for the unique plane in $\mathbb{P}^{3*}$ containing $\Phi^{*}(a^{*})$. Recall that $P^{*}_{a^{*}}$ is identified with $\Phi(a)$ under the natural identification between $\mathbb{P}^{3**}$ and $\mathbb{P}^{3}$. Similarly to the properties of $\Phi$, the full preimage of $P^{*}_{a^{*}}$ under $\Phi^{*}$ is a cubic curve $\varkappa^{*}_{a^{*}}$ consisting of $a^{*}$ and some conic $\sigma^{*}_{a^{*}}$.
Since the topological degree of $\Phi$ is at least two, we know that, for a generic line $a_{1}^{*}\subset\mathbb{P}^{2*}$, there is another line in $\mathbb{P}^{2*}$ mapping to the same plane $P^{*}_{a_{1}^{*}}$ under $\Phi^{*}$. Hence the conic $\sigma^{*}_{a_{1}^{*}}$ splits into the union of two lines. We will write $a_{2}^{*}$ and $a_{3}^{*}$ for these two lines. Thus, the cubic $\varkappa^{*}_{a_{1}^{*}}$ splits into the union of the three lines $a_{1}^{*}$, $a_{2}^{*}$ and $a_{3}^{*}$. Generically, these three lines are different, and they map to the same plane $P^{*}_{a_{1}^{*}}$. This property of $\Phi^{*}$ translates to the following property of $\Phi$: a generic point of $S_{\Phi}$ (corresponding to the plane $P^{*}_{a_{1}^{*}}$) has exactly three preimages $a_{1}$, $a_{2}$, $a_{3}$. $\square$
We also need the following lemma.
Lemma 4.2.
Let $\Phi$ be a strictly cubic$,$ not co-trivial planarization. Suppose a line $\lambda\subset\mathbb{P}^{2}$ does not contain base points of $\Phi$. Then the following assertions hold.
-
1.
The line $\lambda$ cannot be mapped by $\Phi$ to an irreducible conic $;$
-
2.
If the line $\lambda$ is mapped by $\Phi$ to a line $L\subset\mathbb{P}^{3},$ then the map $\Phi|_{\lambda}:\lambda\to L$ is three-to-one.
Proof.
To prove the first assertion, consider a conic $C$ that coincides with $\Phi(\lambda)$. A generic plane $P\subset\mathbb{P}^{3}$ intersects the conic $C$ in two points. The cubic $\varkappa_{P}$ intersects the line $\lambda$ in three points counting multiplicities. Therefore, we must have $3=2k$, where $k$ is the topological degree of the branch covering $\Phi|_{\lambda}:\lambda\to C$. Thus, by way of this contradiction the first assertion is proved.
To prove the second one, consider a point $p\in L$ and a generic plane $P\subset\mathbb{P}^{3}$, such that $P\cap L=p$. We may assume that $\varkappa_{P}=\Phi^{-1}(P)$ is a cubic curve. The set $\varkappa_{P}\cap\lambda$ consists of three points counting multiplicities. Moreover, a multiple intersection point is necessarily a critical point of $\Phi|_{\lambda}$ since the intersection of $P$ and $L$ is transverse. This proves the second assertion. $\square$
Proof of the Main Theorem.
We now assume that $\Phi$ is not dual quadratic. Then, by Proposition 4.1, the topological degree of the map $\Phi:\mathbb{P}^{2}{\setminus}B_{\Phi}\to S_{\Phi}$ is equal to three, and the same is true for the dual planarization $\Phi^{*}$. Let $d$ denote the degree of the surface $\overline{S}_{\Phi}$. By Proposition 2.2, we have $3d=9-|B_{\Phi}|$. It follows that $d$ is at most three, i.e., the surface $\overline{S}_{\Phi}$ is at most cubic.
If the degree of $\overline{S}_{\Phi}$ is at most two, then $\overline{S}_{\Phi}$ must be an irreducible quadric (because we assume $\Phi$ is not trivial). Since the $\Phi$-image of every line is a plane curve, this plane curve must be a conic, possibly degenerate. According to [Timorin2012], Lemma 2.8, such a map $\Phi$ (a rational map of degree at most 3 that takes lines to conics) is a rational map of degree at most two, unless $\Phi(\mathbb{P}^{2}{\setminus}B_{\Phi})$ is contained in a line. Thus, from now on, we may assume that $\overline{S}_{\Phi}$ is a cubic surface.
All of the above is applicable to the dual planarization $\Phi^{*}$. Hence, it follows by Proposition 2.2 that the sets $B_{\Phi}$ and $B_{\Phi^{*}}$ are empty, hence $S_{\Phi}$ (and $S_{\Phi^{*}}$) is compact. It is a classical fact that $S_{\Phi}$ contains at least one line (recall that a smooth cubic surface contains 27 lines, and any cubic surface can be approximated by smooth cubic surfaces). Let $L$ be a line contained in $S_{\Phi}$.
We claim that the set $\Phi^{-1}(L)$ is a union of at most three lines. Indeed, let $L^{*}$ be the line in $\mathbb{P}^{3*}$ consisting of all planes in $\mathbb{P}^{3}$ that contain the line $L$. The line $L^{*}$ must intersect the surface $\Phi^{*}(\mathbb{P}^{2*})$ at some point $b^{*}$. Let $P_{b^{*}}$ be the plane in $\mathbb{P}^{3}$ corresponding to the point $b^{*}\in\mathbb{P}^{3*}$. Clearly, $L\subset P_{b^{*}}$, therefore, $\Phi^{-1}(L)\subset\Phi^{-1}(P_{b^{*}})$ and the set $\Phi^{-1}(P_{b^{*}})$ is the union of at most three lines. Let $\lambda\subset\Phi^{-1}(P_{b^{*}})$ be a line that is mapped to $L$.
We will now argue that this $\lambda$ must be a point of indeterminacy for $\Phi^{*}$. Choose any point $p\in\lambda$ and let $p^{*}$ be the corresponding line in $\mathbb{P}^{2*}$. As a set of lines in $\mathbb{P}^{2}$, it consists of all lines through $p$. In [Timorin2012], Proposition 2.1, a cubic rational map $\Psi_{p^{*}}$ from $p^{*}$ to $\mathbb{P}^{3*}$ was constructed that coincides with $\Phi^{*}$ almost everywhere on $p^{*}$ and that has $\lambda$ as a point of indeterminacy. If $\lambda$ is not a point of indeterminacy for $\Phi^{*}$, then $\Phi^{*}|_{p^{*}}$ must coincide with some quadratic rational map, so that the expression for $\Psi_{p^{*}}$ in homogeneous coordinates has a nontrivial polynomial factor common to all components. The image $\Phi^{*}(p^{*})$ is then a subset of a conic or of a line. The first option is impossible by the first assertion of Lemma 4.2. If $\Phi^{*}(p^{*})$ is a subset of a line, then, by the second assertion of Lemma 4.2 the dual planarization $\Phi^{*}$ must map $p^{*}$ three-to-one to its image. However, this is impossible for a quadratic rational map: the topological degree of a quadratic rational map is at most two.
It follows that $\lambda$ is a point of indeterminacy for $\Phi^{*}$, which contradicts the fact that $B_{\Phi^{*}}=\varnothing$. $\square$
5 Quadratic Planarizations
Throughout this section, we suppose that $\Phi:\mathbb{P}^{2}\dashrightarrow\mathbb{P}^{3}$ is a quadratic rational map such that the image of $\Phi$ lies in some quadratic surface $S$ but does not lie in a plane. We will classify all such quadratic maps up to projective equivalence. The classification must be classical but we failed to find a modern reference. The following theorem describes the classification over $\mathbb{C}$.
Theorem 5.1.
Suppose that the ground field is $\mathbb{C}$. Then $\Phi$ is projectively equivalent to one and only one of the following three maps$:$
| $\displaystyle\Phi_{1}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_{ 2}:x_{1}x_{2}],$ | |||
| $\displaystyle\Phi_{2}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{0}x_{2}],$ | |||
| $\displaystyle\Phi_{3}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}^{2}].$ |
The planarizations $\Phi_{1}$ and $\Phi_{2}$ are co-trivial. The dual planarization of $\Phi_{3}$ is projectively equivalent to $\Phi_{3}$.
The corresponding real classification differs only in that the complex equivalence class of $\Phi_{1}$ splits into two real equivalence classes $\Phi_{1a}$ and $\Phi_{1b}$.
Theorem 5.2.
Suppose that the ground field is $\mathbb{R}$. Then $\Phi$ is projectively equivalent to one and only one of the following four maps$:$
| $\displaystyle\Phi_{1a}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_ {2}:x_{1}x_{2}],$ | |||
| $\displaystyle\Phi_{1b}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_ {2}:x_{1}^{2}+x_{2}^{2}],$ | |||
| $\displaystyle\Phi_{2}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{0}x_{2}],$ | |||
| $\displaystyle\Phi_{3}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}^{2}].$ |
The planarizations $\Phi_{1a},\Phi_{1b}$ and $\Phi_{2}$ are co-trivial. The dual planarization of $\Phi_{3}$ is projectively equivalent to $\Phi_{3}$.
5.1 Complex Classification
In this section, we assume that the ground field is $\mathbb{C}$. The proof of Theorem 5.1 consists of several lemmas. We first assume that the quadric $S$ is non-degenerate.
Lemma 5.3.
If the surface $S$ is given by the equation $u_{0}u_{1}=u_{2}u_{3}$ with respect to some system of homogeneous coordinates $[u_{0}:u_{1}:u_{2}:u_{3}]$ in $\mathbb{P}^{3},$ then $\Phi$ has the form
| $\displaystyle[x_{0}:x_{1}:x_{2}]\mapsto[\psi_{0}\psi_{1}:\psi_{2}\psi_{3}:\psi _{0}\psi_{2}:\psi_{1}\psi_{3}],$ |
where $\psi_{\alpha},\alpha=0,\ldots,3,$are homogeneous linear forms in $x_{0},x_{1},x_{2}.$
Proof.
The map $\Phi$ can be written in coordinates as $u_{\alpha}=\varphi_{\alpha}(x_{0},x_{1},x_{2})$, where $x_{0}$, $x_{1}$, $x_{2}$ are homogeneous coordinates in $\mathbb{P}^{2}$, $\varphi_{\alpha}$ are quadratic forms not vanishing identically, and the index $\alpha$ runs from 0 to 3.
We claim that every quadratic polynomial $\varphi_{\alpha}$ is reducible. Indeed, if one of these polynomials, say, $\varphi_{0}$ is irreducible, then, since $\varphi_{0}\varphi_{1}=\varphi_{2}\varphi_{3}$ by the unique factorization property, $\varphi_{2}$ or $\varphi_{3}$ is divisible by $\varphi_{0}$, hence is proportional to $\varphi_{0}$. It follows however that the image of $\Phi$ lies in a plane, a contradiction. Thus every $\varphi_{\alpha}$ is a product of two linear factors. We write $\varphi_{0}$ as $\psi_{0}\psi_{1}$, where $\psi_{0}$ and $\psi_{1}$ are linear homogeneous polynomials in $x_{0}$, $x_{1}$, $x_{2}$. Then $\varphi_{2}$ or $\varphi_{3}$ is divisible by $\psi_{0}$. Relabeling $\varphi_{2}$ and $\varphi_{3}$ if necessary, we may assume that $\varphi_{2}$ is divisible by $\psi_{0}$. Set $\varphi_{2}=\psi_{0}\psi_{2}$, where $\psi_{2}$ is some linear polynomial. It now follows from the identity $\varphi_{0}\varphi_{1}=\varphi_{2}\varphi_{3}$ that $\psi_{1}\varphi_{1}=\psi_{2}\varphi_{3}$. The forms $\psi_{1}$ and $\psi_{2}$ are not proportional, since otherwise $\varphi_{0}$ and $\varphi_{2}$ are also proportional, and the image of $\Phi$ is a subset of a plane. We see that $\varphi_{3}$ is divisible by $\psi_{1}$, therefore, $\varphi_{3}$ can be written as $\psi_{1}\psi_{3}$. It follows that $\varphi_{1}=\psi_{2}\psi_{3}$. $\square$
We can now classify all maps $\Phi$, for which $S$ is non-singular.
Lemma 5.4.
Suppose that $S$ is nonsingular. Then $\Phi$ is equivalent to the following map$:$
| $\displaystyle\Phi_{1}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_{ 2}:x_{1}x_{2}].$ |
In particular$,$ $\Phi$ is co-trivial.
Proof.
There is a system of homogeneous coordinates $u_{0}$, $u_{1}$, $u_{2}$, $u_{3}$ in the target space $\mathbb{P}^{3}$ such that the surface $S$ is given by the equation $u_{0}u_{1}=u_{2}u_{3}$. By Lemma 5.3, the map $\Phi$ has the form $[x_{0},x_{1},x_{2}]\mapsto[\psi_{0}\psi_{1}:\psi_{2}\psi_{3}:\psi_{0}\psi_{2}: \psi_{1}\psi_{3}]$, where $\psi_{\alpha}$ are linear forms in $x_{0}$, $x_{1}$, $x_{2}$. The set of indeterminacy points of $\Phi$ is equal to $B_{\Phi}=\{\psi_{0}=\psi_{3}=0\}\cup\{\psi_{1}=\psi_{2}=0\}$. Indeed, if $\psi_{0}\neq 0$, then we must have $\psi_{1}=\psi_{2}=0$, and if $\psi_{1}\neq 0$, then we must have $\psi_{0}=\psi_{3}=0$.
We claim that the set $B_{\Phi}$ consists of exactly two points. The system of equations $\psi_{0}=\psi_{3}=0$ defines a point $a$. Indeed, otherwise the linear functionals $\psi_{0}$ and $\psi_{3}$ must be proportional, and we may assume $\psi_{0}=\psi_{3}$. In this case, we have $\varphi_{0}=\varphi_{3}$, which means that the image of $\Phi$ lies in a plane section of $S$, a contradiction with our assumption that $S$ is non-singular. Similarly, the system of equations $\psi_{1}=\psi_{2}=0$ defines a point $b$. It remains to show that $a\neq b$. Indeed, otherwise the map $\Phi$ factors through the central projection of $\mathbb{P}^{2}{\setminus}\{a\}$ onto $\mathbb{P}^{1}$. It follows that the image of $\Phi$ lies in a conic, a contradiction with our assumption. Thus we have $B_{\Phi}=\{a,b\}$.
Consider the linear web of conics $\mathcal{L}_{\Phi}$ associated with $\Phi$. All conics of $\mathcal{L}_{\Phi}$ pass through $a$ and $b$. On the other hand, the linear system $\mathcal{L}$ of all conics passing through $a$ and $b$ has dimension 3. Therefore, $\mathcal{L}_{\Phi}=\mathcal{L}$. We can now choose homogeneous coordinates $[x_{0}:x_{1}:x_{2}]$ in $\mathbb{P}^{2}$ so that $a=[0:1:0]$ and $b=[0:0:1]$. Then $\mathcal{L}$ is spanned by the following degenerate conics: $x_{0}^{2}=0$, $x_{0}x_{1}=0$, $x_{0}x_{2}=0$ and $x_{1}x_{2}=0$. The map $\Phi$ corresponding to this choice of generators coincides with $\Phi_{1}$, as desired. The planarization $\Phi_{1}$ is co-trivial: indeed, every line is mapped under $\Phi_{1}$ to a plane passing through $[0:0:0:1]$. $\square$
Continuing the complex classification of quadratic planarizations, we now assume that $S$ is contained in a degenerate quadric.
Lemma 5.5.
Suppose that $S$ is given by the equation $u_{1}^{2}=u_{0}u_{2}$ with respect to some system of homogeneous coordinates $[u_{0}:u_{1}:u_{2}:u_{3}]$ in $\mathbb{P}^{3}$. Then$,$ possibly after a projective coordinate change in $\mathbb{P}^{2}$ and $\mathbb{P}^{3},$ the map $\Phi$ has the form
| $\displaystyle[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2},\varphi _{3}(x_{0},x_{1},x_{2})],$ |
where $\varphi_{3}$ is some homogeneous quadratic form in the variables $x_{0},x_{1},x_{2}.$
Proof.
Suppose that $\Phi$ is given by the equations $u_{\alpha}=\varphi_{\alpha}(x_{0},x_{1},x_{2})$. As before, we argue that $\varphi_{1}$ is reducible, otherwise it would be proportional either to $\varphi_{0}$ or to $\varphi_{2}$. Similarly, $\varphi_{0}$ and $\varphi_{2}$ are reducible. We can write $\varphi_{1}$ as $\psi_{0}\psi_{1}$, where $\psi_{0}$ and $\psi_{1}$ are linear functions. Then $\varphi_{0}$ or $\varphi_{2}$ is divisible by $\psi_{0}$; we may assume the former and write $\varphi_{0}=\psi_{0}\tilde{\psi}_{0}$. It follows from the equation $\varphi_{1}^{2}=\varphi_{0}\varphi_{2}$ that $\psi_{0}\psi_{1}^{2}=\tilde{\psi}_{0}\varphi_{2}$. Therefore, $\tilde{\psi}_{0}$ is proportional to $\psi_{0}$ or to $\psi_{1}$. In the former case, we have $\varphi_{0}=\psi_{0}^{2}$ and $\varphi_{2}=\psi_{1}^{2}$, up to a projective coordinate change in $\mathbb{P}^{3}$ (multiplying the homogeneous coordinates by different constants). In the latter case, $\varphi_{0}$ would be proportional to $\varphi_{1}$, a contradiction with our assumption.
Thus we have $\varphi_{1}=\psi_{0}\psi_{1}$, $\varphi_{0}=\psi_{0}^{2}$, $\varphi_{2}=\psi_{1}^{2}$ for some non-proportional linear forms $\psi_{0}$, $\psi_{1}$. We can choose the homogeneous coordinates $[x_{0}:x_{1}:x_{2}]$ in $\mathbb{P}^{2}$ so that $\psi_{0}=x_{0}$ and $\psi_{1}=x_{1}$. The map $\Phi$ now takes the form $[x_{0}:x_{1}:x_{3}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2}:\varphi_{3}(x_{0},x_ {1},x_{2})]$, where $\varphi_{3}$ is a quadratic form in the variables $x_{0}$, $x_{1}$, $x_{2}$, as desired. $\square$
The following lemma provides normal forms for $\Phi$ in the case, where $S$ is an irreducible cone.
Lemma 5.6.
Suppose that $S$ is a singular irreducible quadric$,$ i.e.$,$ a quadratic cone. Then $\Phi$ is equivalent to at least one of the maps
| $\displaystyle\Phi_{2}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}x_{0}]$ | |||
| $\displaystyle\Phi_{3}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}^{2}].$ |
Proof.
There is a homogeneous coordinate system $u_{0}$, $u_{1}$, $u_{2}$, $u_{3}$ in the space $\mathbb{P}^{3}$ such that the cone $S$ is given by the equation $u_{1}^{2}=u_{0}u_{2}$. By Lemma 5.5, we may assume that the map $\Phi$ has the form $[x_{0}:x_{1}:x_{3}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2}:\varphi_{3}(x_{0},x_ {1},x_{2})]$, where $\varphi_{3}$ is a quadratic form in the variables $x_{0}$, $x_{1}$, $x_{2}$. We may change $\varphi_{3}$ by adding any linear combination of $x_{0}^{2}$, $x_{0}x_{1}$, $x_{1}^{2}$, i.e., by adding any quadratic form in $x_{0}$, $x_{1}$ only: this can be implemented by means of a projective coordinate change in the target space $\mathbb{P}^{3}$. Thus we may assume that $\varphi_{3}(x_{0},x_{1},x_{2})=x_{2}(a_{0}x_{0}+a_{1}x_{1}+a_{2}x_{2})$.
Suppose first that $a_{2}=0$. Then at least one of the coefficients $a_{0}$, $a_{1}$ is nonzero. Assume e.g. that $a_{0}\neq 0$ (the case $a_{1}\neq 0$ is obtained from this case by interchanging $x_{0}$ and $x_{1}$). Then we set $\widetilde{x}_{0}=a_{0}x_{0}+a_{1}x_{1}$, $\widetilde{x}_{1}=x_{1}$, $\widetilde{x}_{2}=x_{2}$. In the new variables, the map $\Phi$ has the form $\Phi:[\widetilde{x}_{0}:\widetilde{x}_{1}:\widetilde{x}_{2}]\mapsto[U_{0}:U_{1 }:U_{2}:\widetilde{x}_{2}\widetilde{x}_{0}]$, where $U_{0}$, $U_{1}$ and $U_{2}$ are linearly independent quadratic forms in $\widetilde{x}_{0}$, $\widetilde{x}_{1}$. Since the space of quadratic forms in $\widetilde{x}_{0}$, $\widetilde{x}_{1}$ is three-dimensional, the monomials $\widetilde{x}_{0}^{2}$, $\widetilde{x}_{0}\widetilde{x}_{1}$, $\widetilde{x}_{1}^{2}$ can be represented as linear combinations of $U_{0}$, $U_{1}$, $U_{2}$. Therefore, changing homogeneous coordinates in the target space $\mathbb{P}^{3}$, we can reduce $\Phi$ to the form $\Phi:[\widetilde{x}_{0}:\widetilde{x}_{1}:\widetilde{x}_{2}]\mapsto[\widetilde {x}_{0}^{2}:\widetilde{x}_{0}\widetilde{x}_{1}:\widetilde{x}_{1}^{2}: \widetilde{x}_{2}\widetilde{x}_{0}]$, i.e., to the form $\Phi_{2}$.
Suppose now that $a_{2}\neq 0$. Then we make the following change of variables: $x_{0}=\widetilde{x}_{0}$, $x_{1}=\widetilde{x}_{1}$, $x_{2}=c_{0}\widetilde{x}_{0}+c_{1}\widetilde{x}_{1}+c_{2}\widetilde{x}_{2}$. In the new variables, the map $\Phi$ has the form
| $\displaystyle[\widetilde{x}_{0}:\widetilde{x}_{1}:\widetilde{x}_{2}]\mapsto[ \widetilde{x}_{0}^{2}:\widetilde{x}_{0}\widetilde{x}_{1}:\widetilde{x}_{1}^{2} :\widetilde{\varphi}_{3}(\widetilde{x}_{0},\widetilde{x}_{1},\widetilde{x}_{2} )],$ | |||
| $\displaystyle\widetilde{\varphi}_{3}(\widetilde{x}_{0},\widetilde{x}_{1}, \widetilde{x}_{2})=(c_{0}\widetilde{x}_{0}+c_{1}\widetilde{x}_{1}+c_{2} \widetilde{x}_{2})((a_{0}+a_{2}c_{0})\widetilde{x}_{0}+(a_{1}+a_{2}c_{1}) \widetilde{x}_{1}+a_{2}c_{2}\widetilde{x}_{2})$ | |||
| $\displaystyle\quad=c_{2}\widetilde{x}_{2}((a_{0}+2a_{2}c_{0})\widetilde{x}_{0} +(a_{1}+2a_{2}c_{1})\widetilde{x}_{1}+a_{2}c_{2}\widetilde{x}_{2})+\cdots$ |
The dots mean a quadratic form in $\widetilde{x}_{0}$, $\widetilde{x}_{1}$. We now set
| $\displaystyle c_{0}=-\frac{a_{0}}{2a_{2}},\quad c_{1}=-\frac{a_{1}}{2a_{2}}, \quad c_{2}=\frac{1}{\sqrt{a_{2}}}$ |
(we choose any one of the two complex values of $\sqrt{a_{2}}$). Then we have $\widetilde{\varphi}_{3}=\widetilde{x}_{2}^{2}+\cdots$, where dots mean a quadratic form in $\widetilde{x}_{0}$, $\widetilde{x}_{1}$. The latter can be killed by a suitable change of variables in the target space (more precisely, by adding a certain linear combination of the coordinates $u_{0}$, $u_{1}$, $u_{2}$ to the last coordinate $u_{3}$). Thus we reduced $\Phi$ to the form $[\widetilde{x}_{0}:\widetilde{x}_{1}:\widetilde{x}_{2}]\mapsto[\widetilde{x}_{ 0}^{2}:\widetilde{x}_{0}\widetilde{x}_{1}:\widetilde{x}_{1}^{2}:\widetilde{x}_ {2}^{2}]$, i.e., to the form $\Phi_{3}$. $\square$
Proof of Theorem 5.1.
Finally, we need to distinguish between $\Phi_{2}$ and $\Phi_{3}$, i.e., to prove that these two maps are not equivalent. To this end, it suffices to compute the dual planarizations of $\Phi_{2}$ and $\Phi_{3}$ and observe that equivalent planarizations must have equivalent dual planarizations. The planarization $\Phi_{2}$ is co-trivial: the image of every line is contained in a plane passing through $[0:0:1:0]$. On the other hand, a straightforward computation shows that the dual planarization of $\Phi_{3}$ is equivalent to $\Phi_{3}$, in particular, is not trivial. This concludes the proof of Theorem 5.1. $\square$
5.2 Real Classification
In this subsection, we assume that the ground field is $\mathbb{R}$. The proof of Theorem 5.2 splits into the following two lemmas.
Lemma 5.7.
Suppose that $S$ is nonsingular. Then $\Phi$ is equivalent to one and only one of the following maps$:$
| $\displaystyle\Phi_{1a}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_ {2}:x_{1}x_{2}],$ | |||
| $\displaystyle\Phi_{1b}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{0}x_ {2}:x_{1}^{2}+x_{2}^{2}].$ |
Proof.
Consider the linear web of conics $\mathcal{L}_{\Phi}$ associated with the complexification of $\Phi$. By the proof of Lemma 5.4, the web $\mathcal{L}_{\Phi}$ has two different complex base points $a\neq b$ and consists of all conics passing through $a$ and $b$. There are two possibilities: $a$ and $b$ can be real or complex conjugate. Suppose first that $a$ and $b$ are real. Then, as in the proof of Lemma 5.4, we show that $\Phi$ is equivalent to $\Phi_{1a}$. Suppose now that $a$ and $b$ are complex conjugate. Performing a suitable change of homogeneous coordinates $[x_{0}:x_{1}:x_{2}]$ in $\mathbb{P}^{2}$ over real numbers, we may assume that $a=[0:1:i]$ and $b=[0:1:-i]$. Then the web of all conics passing through $a$ and $b$ is spanned by the degenerate conics $x_{0}^{2}=0$, $x_{0}x_{1}=0$, $x_{0}x_{2}=0$ and $x_{1}^{2}+x_{2}^{2}=0$. Indeed, these four degenerate conics are given by linearly independent quadratic forms and do pass through $a$ and $b$. Note that, in the affine chart $x_{0}=1$ with affine coordinates $x_{1}$, $x_{2}$, the web $\mathcal{L}_{\Phi}$ is exactly the web of all circles (including degenerate ones). With this choice of generating conics, $\Phi$ coincides with $\Phi_{1b}$.
The maps $\Phi_{1a}$ and $\Phi_{1b}$ are not equivalent over reals because the corresponding linear webs of conics have different number of real base points. $\square$
Lemma 5.8.
Suppose that $S$ is singular but irreducible. Then $\Phi$ is equivalent to one and only one of the following maps$:$
| $\displaystyle\Phi_{2}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}x_{0}]$ | |||
| $\displaystyle\Phi_{3}:[x_{0}:x_{1}:x_{2}]\mapsto[x_{0}^{2}:x_{0}x_{1}:x_{1}^{2 }:x_{2}^{2}].$ |
Proof.
The proof of Lemma 5.6 applies verbatim over reals, except that it is not always possible to take $\sqrt{a_{2}}$. If $a_{2}<0$, then we set instead $c_{2}=1/\sqrt{-a_{2}}$ and reduce $\Phi$ to the form $[\widetilde{x}_{0}:\widetilde{x}_{1}:\widetilde{x}_{2}]\mapsto[\widetilde{x}_{ 0}^{2}:\widetilde{x}_{0}\widetilde{x}_{1}:\widetilde{x}_{1}^{2}:-\widetilde{x} _{2}^{2}]$. However, changing sign of the last coordinate in $\mathbb{P}^{3}$ gets it back to the form $\Phi_{3}$. Since $\Phi_{2}$ and $\Phi_{3}$ are not equivalent over complex numbers, neither are they over reals. $\square$
6 Normal Forms of Planarizations
In this section, we give a complete list of local normal forms of planarizations. We assume that the ground field is $\mathbb{R}$.
Theorem 6.1.
Suppose that $U\subset\mathbb{P}^{2}$ is an open subset and $\Phi:U\to\mathbb{P}^{3}$ is
a planarization. Then$,$ for every open subset $V\subset U$ there
exists a $($possibly smaller$)$ open subset $W\subset V$ such that
$\Phi:W\to\mathbb{P}^{3}$ is projectively equivalent to at least one of the
following normal forms$:$
$(T){:}$
$[x:y:z]\mapsto[f(x,y,z):g(x,y,z):h(x,y,z):0]$
$(CT){:}$
$[x:y:z]\mapsto[x:y:z:f(x,y,z)]$
$(Q_{1}){:}$
$[x:y:z]\mapsto[xy:xz:yz:x^{2}+y^{2}+z^{2}]$
$(Q_{2}){:}$
$[x:y:z]\mapsto[xy:xz:yz:x^{2}-y^{2}+z^{2}]$
$(Q_{3}){:}$
$[x:y:z]\mapsto[x^{2}+y^{2}:y^{2}+z^{2}:xz:yz]$
$(Q_{4}){:}$
$[x:y:z]\mapsto[x^{2}-y^{2}:xy:yz:z^{2}]$
$(Q_{5}){:}$
$[x:y:z]\mapsto[xz-yz:x^{2}:y^{2}:z^{2}]$
$(Q_{6}){:}$
$[x:y:z]\mapsto[x^{2}:xz-y^{2}:yz:z^{2}]$
$(Q_{7}){:}$
$[x:y:z]\mapsto[y^{2}-z^{2}:xy:xz:yz]$
$(Q_{8}){:}$
$[x:y:z]\mapsto[xy:xz:y^{2}:z^{2}]$
$(Q_{9}){:}$
$[x:y:z]\mapsto[xy:xz-y^{2}:yz:z^{2}]$
$(Q_{10}){:}$
$[x:y:z]\mapsto[x^{2}:xy:y^{2}:z^{2}]$
$(C_{1}){:}$
$[x:y:z]\mapsto[z(x^{2}+y^{2}):y(x^{2}+z^{2}):x(y^{2}+z^{2}):xyz]$
$(C_{2}){:}$
$[x:y:z]\mapsto[z(x^{2}-y^{2}):y(x^{2}+z^{2}):x(y^{2}-z^{2}):xyz]$
$(C_{3}){:}$
$[x:y:z]\mapsto[x^{2}z:z(x^{2}+y^{2}):x(x^{2}+y^{2}-z^{2}):y(x^{2}+y^{2}+z^{2})]$
$(C_{4}){:}$
$[x:y:z]\mapsto[x^{2}y:x(x^{2}-y^{2}):z(x^{2}+y^{2}):yz^{2}]$
$(C_{5}){:}$
$[x:y:z]\mapsto[x^{2}(x+y):y^{2}(x+y):z^{2}(x-y):xyz]$
$(C_{6}){:}$
$[x:y:z]\mapsto[x^{3}:xy^{2}:2xyz-y^{3}:z(xz-y^{2})]$.
Here $f,g$ and $h$ are sufficiently smooth degree 1
homogeneous functions of $x,y,z$. In normal form $(T),$ the
mapping $[x:y:z]\mapsto[f:g:h]$ represents an arbitrary
sufficiently smooth embedding of $W$ into $\mathbb{P}^{2}$.
In Theorem 6.1, the form $(T)$ represents all trivial planarizations, and the form $(CT)$ represents all co-trivial planarizations that are not trivial. These items correspond to infinitely many projective equivalence classes. However, note that there are finitely many classes of nontrivial non-co-trivial planarizations.
Proof.
By the Main Theorem, every point $a\in U$ has a neighborhood $V\subset U$ such that the planarization $\Phi:V\to\mathbb{P}^{3}$ is trivial, co-trivial, quadratic or dual quadratic. Suppose first that $\Phi:V\to\mathbb{P}^{3}$ is trivial. This means by definition that there is a plane $P\subset\mathbb{P}^{3}$ such that $\Phi(V)\subset P$. By a projective coordinate change, we may assume that the plane $P$ is given in homogeneous coordinates $[u_{0}:u_{1}:u_{2}:u_{3}]$ by $u_{3}=0$. Then the map $\Phi:V\to\mathbb{P}^{3}$ has form $(T)$.
Suppose now that the planarization $\Phi:V\to\mathbb{P}^{3}$ is co-trivial but not trivial. Then, by definition, there is a point $b\in\mathbb{P}^{3}$ such that, for every line $L\subset\mathbb{P}^{2}$, there is a plane $P_{L}$ containing the set $\Phi(L\cap V)\cup\{b\}$. We may assume that $b=[0:0:0:1]$. There is a nonempty open subset $W\subset V$ such that $\Phi(W)\not\ni b$. Let $\mathbb{P}^{2}(b)$ be the projective plane formed by all lines in $\mathbb{P}^{3}$ passing through $b$, and let $\pi:\mathbb{P}^{3}{\setminus}\{b\}\to\mathbb{P}^{2}(b)$ be the canonical projection mapping a point $c\neq b$ to the line $bc$. Note that the map $\Psi=\pi\circ\Phi:W\to\mathbb{P}^{2}(b)$ has the following property. For every line $L\subset\mathbb{P}^{2}$, the set $\Psi(W\cap L)$ is a subset of a line. By the Möbius–von Staudt theorem, a map with this property must be a restriction of a projective transformation or a mapping from $W$ to a line, possibly after replacing $W$ with a smaller open set. In the second case, $\Phi:W\to\mathbb{P}^{3}$ is trivial, and therefore is equivalent to the form $(T)$. In the first case, the map $\Psi$ is given by $[x:y:z]\mapsto[x:y:z]$ provided that we choose a suitable system of projective coordinates in $\mathbb{P}^{2}(b)$. Then the map $\Phi:W\to\mathbb{P}^{3}$ is given by $[x:y:z]\mapsto[x:y:z:f(x,y,z)]$ for some (sufficiently smooth) function $f$.
Suppose now that the planarization $\Phi:V\to\mathbb{P}^{3}$ is quadratic but neither trivial nor co-trivial. Note that the image $\Phi(V)$ lies in a surface $S$ of degree 2, 3 or 4. Indeed, since $\Phi$ is not trivial, the degree is greater than one; on the other hand, the image of the plane under a quadratic rational map lies in a surface of degree at most four. If $S$ has degree 2, then $\Phi$ is equivalent to one of the maps $\Phi_{1a}$, $\Phi_{1b}$, $\Phi_{2}$, $\Phi_{3}$ from Theorem 5.2. Since, by our assumption, $\Phi$ is not co-trivial, it must be equivalent to $\Phi_{3}$; the latter is redenoted by $(Q_{10})$ in the statement of the theorem. Suppose now that $S$ has degree 3 or 4. In this case, we refer to the results of [Coffman et al.1996]. By [Coffman et al.1996], every quadratic rational map $\Phi$ such that $\Phi(\mathbb{P}^{2}{\setminus}B_{\Phi})$ is dense in a surface of degree 3 or 4 is equivalent to one of the maps $(Q_{1})$–$(Q_{9})$.
Finally, suppose that the planarization $\Phi:V\to\mathbb{P}^{3}$ is dual quadratic but not trivial, not co-trivial, and not quadratic. Then its dual planarization is equivalent to one of the maps $(Q_{1})$–$(Q_{9})$. A straightforward computation shows that the dual planarizations to $(Q_{1})$–$(Q_{6})$ are equivalent, respectively, to $(C_{1})$–$(C_{6})$. The planarizations $(Q_{7})$–$(Q_{9})$, characterized by the property that the corresponding surfaces in $\mathbb{P}^{3}$ are cubic, turn out to be equivalent to their dual planarizations. In particular, the dual planarizations of $(Q_{7})$–$(Q_{9})$ are quadratic. $\square$
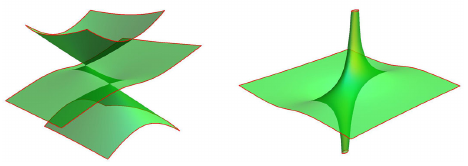
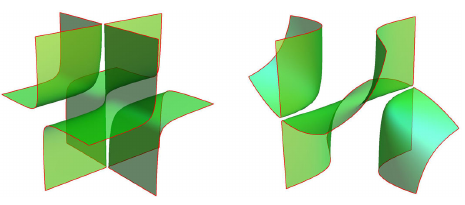
The equations of the surfaces parameterized by dual-quadratic planarizations $(C_{1})$–$(C_{6})$ are
$(C_{1})$: $4t^{3}-t(u^{2}+v^{2}+w^{2})+uvw=0$
$(C_{2})$: $4t^{3}+t(u^{2}-v^{2}+w^{2})+uvw=0$
$(C_{3})$: $4vu^{2}+u(t^{2}-4v^{2}+w^{2})-vw^{2}=0$
$(C_{4})$: $4tu^{2}-uw^{2}+tv^{2}=0$
$(C_{5})$: $u(vw-t^{2})+vt^{2}=0$
$(C_{6})$:
$u(4tv-w^{2})+v^{3}=0$,
where $[u:v:w:t]$ are homogeneous coordinates in $\mathbb{P}^{3}$. These
equations are obtained by eliminating the three variables $x$, $y$,
$z$ from the four equations
We used Mathematica to perform the computations. We provide
figures of these surfaces below, see Figs. 1, 2 and 3.
$\displaystyle[u:v:w:t]=\Phi[x:y:z].$
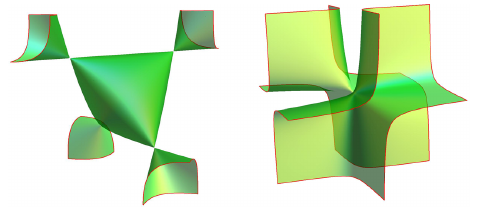
References
- [Beauville1996] Beauville, A.: Complex Algebraic Surfaces. Cambridge University Press, Cambridge (1996)
- [Coffman et al.1996] Coffman, A., Schwartz, A., Stanton, C.: The algebra and geometry of Steiner and other quadratically parametrizable surfaces. Comput. Aided Geom. Des. 13, 257–286 (1996)
- [Deng et al.2011] Deng, B., Pottmann, H., Wallner, J.: Functional webs for freeform architecture. Comput. Graph. Forum 30(5), 1369–1378 (2011)
- [Izadi2005] Izadi, F.A.: On rectification of circles and an extension of Beltrami’s theorem. Rocky Mt. J. Math. 34(3), 881–899 (2005)
- [Khovanskii1976] Khovanskii, G.S.: Foundations of Nomography (in Russian). Nauka, Moscow (1976)
- [Khovanskii1980] Khovanskii, A.G.: Rectification of circles. Sib. Math. J. 21, 649–652 (1980)
- [Möbius1885] Möbius, A.F.: Der barycentrische Calcul, 1827, In: Hirzel, S. (ed.) August Ferdinand Möbius, gesammelte Werke, vol. 1. Leipzig (1885)
- [Mumford1976] Mumford, D.: Algebraic Geometry I: Complex Projective Varieties. Springer, Berlin (1976)
- [Timorin2003] Timorin, V.: Rectification of circles and quaternions. Mich. Math. J. 51, 153–167 (2003)
- [Timorin2004] Timorin, V.: Circles and clifford algebras. Funct. Anal. Appl. 38(1), 45–51 (2004)
- [Timorin2005] Timorin, V.: Circles and quadratic maps between spheres. Geometriae Dedicata 115, 19–32 (2005)
- [Timorin2006] Timorin, V.: Maps that take lines to circles, in dimension 4. Funct. Anal. Appl. 40(2), 108–116 (2006)
- [Timorin2012] Timorin, V.: Planarizations and maps taking lines to linear webs of conics. Math. Res. Lett. 19(4), 899–907 (2012)
- [von Staudt1847] von Staudt, KGCh.: Geometrie der Lage. Verlag von Bauer und Raspe, Nürnberg (1847)