Volumes of Strata of Abelian Differentials
and Siegel–Veech Constants in Large Genera
eskin@math.uchicago.edu Anton Zorich Institut de mathématiques de Jussieu Institut Universitaire de France Université Paris 7 Paris France
Anton.Zorich@gmail.com
Abstract
We state conjectures on the asymptotic behavior of the volumes of moduli spaces of Abelian differentials and their Siegel–Veech constants as genus tends to infinity. We provide certain numerical evidence, describe recent advances and the state of the art towards proving these conjectures.
Keywords
Introduction
The first efficient approach for computing volumes of the strata in the moduli spaces of Abelian differentials was found by [Eskin and Okounkov2001] about 15 years ago. The algorithm was implemented by A. Eskin in a rather efficient computer code which already at this time allowed to compute volumes of all strata up to genus 10, and volumes of some strata, like the principal one, up to genus 60 (or more).
About the same time together with H. Masur we expressed the Siegel–Veech constant $c_{\mathit{area}}$ of any stratum of Abelian differentials in terms of an explicit polynomial in volumes of the “principal boundary” strata devided by the volume of the the original stratum, see [Eskin et al.2003]. The sum of the Lyapunov exponents of the Hodge bundle over the Teichmüller geodesic flow can be expressed by a simple formula in terms of the Siegel–Veech constant $c_{\mathit{area}}$ [this formula, is recently proved by M. Kontsevich and the authors in [Eskin et al.2014]].
Direct computations of volumes of the strata in genera accessible at this time combined with numerical experiments with the Lyapunov exponents providing an approximate value of $c_{\mathit{area}}$ inspired two conjectures on asymptotic behavior of volumes of the strata and of the corresponding Siegel–Veech constant $c_{\mathit{area}}$; these conjectures were stated at the end of 2003.
During the last decade we have shared this conjecture with colleagues who were interested in it, but the fact that it was never published lead to some misinterpretations due to misundersting in conventions on normalization. Now, when the formula [Eskin et al.2014] for the sum of the Lyapunov exponents is finally proved, the conjectures become much more important. Besides, there are recent encouraging advances with these conjectures, so it is an occasion to state the conjectures and describe the state of the art.
1 Background Material and Motivations
Holomorphic 1-forms on a given Riemann surface $C$ of genus $g$ form a complex $g$-dimensional vector space, so the moduli space ${\mathcal{H}}$ of pairs (Riemann surface $C$, holomorphic 1-form $\omega$ on $C$) is a total space of complex $g$-dimensional Hodge bundle over the moduli space of complex curves ${\mathcal{M}}_{g}$. The moduli space ${\mathcal{H}}$ is called the moduli space of Abelian differentials. A holomorphic 1-form $\omega$ on a Riemann surface of genus $g$ has $2g-2$ zeroes counting multiplicities. For example, a holomorphic 1-form on a Riemann surface of genus two might have either two simple zeroes or a single zero of order 2. The moduli space ${\mathcal{H}}$ gets naturally stratified by the strata ${\mathcal{H}}(m_{1},\dots,m_{n})$ of pairs (Riemann surface $C$, holomorphic 1-form $\omega$ on $C$ with zeroes of orders $m_{1},\dots,m_{n}$), where $m_{1}+\dots+m_{n}=2g-2$. For example, in genus two there are only two such strata, namely, the principal stratum ${\mathcal{H}}(1,1)$ and the stratum ${\mathcal{H}}(2)$.
Note that, in general, individual strata do not carry any bundle structure over ${\mathcal{M}}_{g}$. The dimension of the stratum is computed as
| $\displaystyle\dim_{{\mathbb{C}}}{\mathcal{H}}(m_{1},\dots,m_{n})=2g+n-1\,.$ |
In particular, the dimension of the minimal stratum ${\mathcal{H}}(2g-2)$ is $2g$ while the dimension of the moduli space of curves ${\mathcal{M}}_{g}$ is $3g-3$.
The strata are not necessarily connected: they might have up to three connected components. In genera greater than or equal to four the classifying invariants are the parity of the spin structure applicable to strata ${\mathcal{H}}(2k_{1},\dots,2k_{n})$ for which all entries $m_{i}=2k_{i}$ are even, and hyperellipticity applicable to two special strata, namely, to ${\mathcal{H}}(g-1,g-1)$ and to ${\mathcal{H}}(2g-2)$, see [Kontsevich and Zorich2003].
Denote by $P_{1},\dots,P_{n}\in C$ the points of the Riemann surface $C$, where the holomorphic 1-form has zeroes. The vector space $H^{1}(C,\{P_{1},\dots,P_{n}\};{\mathbb{C}})$ provides canonical local period coordinates in the stratum ${\mathcal{H}}(m_{1},\dots,m_{n})$. The lattice $H^{1}(C,\{P_{1},\dots,P_{n}\};{\mathbb{Z}}\oplus i{\mathbb{Z}})$ defines a canonical volume element $d\nu$ in the stratum. This volume element induces a natural volume element on the real hypersurface ${\mathcal{H}}_{1}(m_{1},\dots,m_{n})\subset{\mathcal{H}}(m_{1},\dots,m_{n})$ given by the equation
| $\displaystyle\frac{i}{2}\int_{C}\omega\wedge\bar{\omega}=1\,.$ |
The group $\operatorname{GL}^{+}(2,{\mathbb{R}})$ acts naturally on every stratum: in period coordinates
| $\displaystyle H^{1}(C,\{P_{1},\ldots,P_{n}\};{\mathbb{C}})\simeq H^{1}(C,\{P_{ 1},\ldots,P_{n}\};{\mathbb{R}})\otimes{\mathbb{R}}^{2}$ |
$\operatorname{GL}^{+}(2,{\mathbb{R}})$ acts on the second term in the tensor product. The subgroup $\operatorname{SL}(2,{\mathbb{R}})$ preserves the volume element $d\nu_{1}$. By the fundamental theorem of Masur ([Masur1982]) and Veech ([Veech1982]) the total volume $\nu_{1}({\mathcal{H}}_{1}(m_{1},\dots,m_{n}))$ of any stratum is finite, and the action of $\operatorname{SL}(2,{\mathbb{R}})$ is ergodic on every connected component of the stratum with respect to the invariant measure $d\nu_{1}$.
A holomorphic 1-form $\omega$ defines a flat metric on a Riemann surface $C$ with conical singularities at the zeroes of $\omega$. Such flat metrics appear, for example, by unfolding rational billiard tables. It is very useful to apply the following technology in the study of behavior of geodesics on flat surfaces of this kind. Consider the $\operatorname{GL}^{+}(2,{\mathbb{R}})$-orbit of the point $(C,\omega)$ in the ambient stratum of Abelian differentials and find the orbit closure $\overline{\operatorname{GL}^{+}(2,{\mathbb{R}})\cdot(C,\omega)}$. The geometry of the orbit closure provides you with important information on geometry and dynamics of the original flat surface. The theorem of H. Masur and of W. Veech tells that for almost all flat surfaces in each stratum, such orbit closure is the entire ambient connected component of the stratum. In particular, several important characteristics of individual flat surfaces (such as Siegel–Veech constants discussed in Sect. 3) are expressed in terms of the volumes of the connected components of the strata.
For a deeper presentation of these ideas we recommend a short and extremely accessible introductory article [Wright2016] and more detailed survey papers [Masur and Tabachnikov2002], [Wright2015], [Zorich2006].
2 Conjectural Asymptotics for the Volumes of the Strata of Abelian Differentials
Let $m=(m_{1},\ldots,m_{n})$ be an unordered partition of an even number $2g-2$, i.e., let $|m|=m_{1}+\dots+m_{n}=2g-2$. Denote by $\Pi_{2g-2}$ the set of all such partitions.
Main Conjecture 1.
For any $m\in\Pi_{2g-2}$ one has
| $\operatorname{Vol}{\mathcal{H}}_{1}(m_{1},\ldots,m_{n})=\cfrac{4}{(m_{1}+1) \cdot\dots\cdot(m_{n}+1)}\cdot(1+\varepsilon_{1}(m)),$ | (1) |
where
| $\displaystyle\lim_{g\to\infty}\max_{m\in\Pi_{2g-2}}|\varepsilon_{1}(m)|=0.$ |
Remark 1.
It was proved in [Eskin and Okounkov2001] that for any partition $m\in\Pi_{2g}$ one has
| $\displaystyle\cfrac{\operatorname{Vol}{\mathcal{H}}_{1}(m_{1},\dots,m_{n})}{ \pi^{2g}}\in{\mathbb{Q}}.$ |
Note, however, that the number $\pi$ is not involved in the asymptotic formula (1) anymore.
Remark 2.
We use the normalization of volumes from [Eskin et al.2003]. In particular, all the zeroes are “named”. In notations of [Eskin and Okounkov2001] the formula for the volume should be read as
| $\operatorname{Vol}({\mathcal{H}}_{1}(m))=2\cdot{\bf c}(m+\vec{1})$ |
We conjecture that convergence (1) is sufficiently fast.
Conjecture 1.
There exists a universal constant $C$ such that for all $g$ and all $m\in\Pi_{g}$ one has
| $|\epsilon_{1}(m)|\leq\frac{C}{\sqrt{g}}\,.$ | (2) |
Consider any fixed collection of positive integers $m_{1},..,m_{n}$, and let $|m|=m_{1}+\dots+m_{n}$. For any integer $g$ such that $2g-2>|m|$ define $m(g)$ as $m$ completed by $2g-2-|m|$ entries 1,
| $m(g):=(m_{1},\dots,m_{n},\underbrace{1,\dots,1}_{2g-2-|m|})$ | (3) |
We expect that the convergence is faster than (2) for strata (3) when $g\to+\infty$.
Remark 3.
In the conjectures above we considered the asymptotics with respect to the genus $g$ of the stratum. We could also consider the asymptotics with respect to the dimension of the stratum. Since the complex dimensions of the strata in a given genus $g$ vary from $2g$ to $4g-3$ the corresponding asymptotics are, basically, equivalent.
Note that some strata of Abelian differentials contain several connected components [Kontsevich and Zorich2003]. The conjecture on the asymptotics of the volumes is stated for the total volume of such strata. However, it can be easily specified for the individual components. The result in [Athreya et al.2012] provides the exact value for the hyperelliptic connected components (and, more generally, for all hyperelliptic loci), namely:
| $\displaystyle\operatorname{Vol}{\mathcal{H}}^{hyp}_{1}(2g-2)$ | $\displaystyle=\cfrac{2\pi^{2g}}{(2g+1)!}\cdot\cfrac{(2g-3)!!}{(2g-2)!!}\sim \cfrac{1}{\pi^{2}g}\left(\frac{\pi e}{2g+1}\right)^{2g+1}\,.$ | ||
| $\displaystyle\operatorname{Vol}{\mathcal{H}}^{hyp}_{1}(g-1,g-1)$ | $\displaystyle=\cfrac{4\pi^{2g}}{(2g+2)!}\cdot\cfrac{(2g-2)!!}{(2g-1)!!}\sim \cfrac{1}{\pi^{2}g}\left(\frac{\pi e}{2g+2}\right)^{2g+2}\,.$ |
The above formulae show that the volume of the hyperelliptic connected components is negligible in comparison with the conjectural volume (1) of the stratum when genus is sufficiently large.
Conjecture 2.
For any $k\in\Pi_{g-1}$ one has
| $\cfrac{\operatorname{Vol}{\mathcal{H}}^{even}_{1}(2k_{1},\dots,2k_{n})}{ \operatorname{Vol}{\mathcal{H}}^{odd}_{1}(2k_{1},\dots,2k_{n})}=(1+\varepsilon _{2}(k)),$ | (4) |
where
| $\displaystyle\lim_{g\to\infty}\max_{k\in\Pi_{g-1}}\varepsilon_{2}(k)=0.$ |
This Conjecture might be approached by a crude estimate since we expect that the difference between $\operatorname{Vol}{\mathcal{H}}^{even}_{1}(2k_{1},\dots,2k_{n})$ and $\operatorname{Vol}{\mathcal{H}}^{odd}_{1}(2k_{1},\dots,2k_{n})$ is much smaller than their values.
2.1 Numerical Evidence
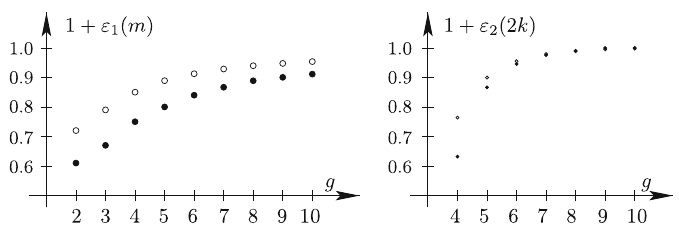
Actually, in the context of the Main Conjecture 1, the infinity does not seem to be very far. We present in Fig. 1 the graphs of exact numerical data for
| $\displaystyle\max_{m\in\Pi_{2g-2}}\left(1+\epsilon_{i}(m)\right)\text{ and } \min_{m\in\Pi_{2g-2}}\left(1+\epsilon_{i}(m)\right),\ i=1,2\,.$ |
for genera $g\leq 10$. The reader can see that at least for this range of genera, one always has $\epsilon_{i}(m)<0$ and that both maximal and minimal value of $\epsilon_{i}(m)$ over all strata in a given genus monotonously tend to zero as genus grows.
For any given genus in the range $2\leq g\leq 10$ the minimum of $|\epsilon_{1}(m)|$ is always attained on the principal stratum ${\mathcal{H}}(1^{2g-2})$ and the maximum of $|\epsilon_{1}(m)|$ is always attained on the (non connected for $g>2$) stratum ${\mathcal{H}}(2g-2)$. In other words (at least for this range of genera) the convergence in (1) is the best for the principal stratum and the worst for the disconnected stratum ${\mathcal{H}}(2g-2)$.
We have $\epsilon_{2}(2k)<0$ for all partitions $k$ in genera in the range from 4 to 10. The minimum of $|\epsilon_{2}(2k)|$ [best convergence in (4)] over all partitions $k\in\Pi_{g-1}$ for any fixed genus in this range is always attained on the stratum ${\mathcal{H}}(2^{g-1})$ and the maximum of $|\epsilon_{2}(2k)|$ (worst convergence in (4)) is always attained on the stratum ${\mathcal{H}}(2g-2)$.
2.2 State of the Art
The Main Conjecture 1 was recently proved by Chen, Möller and Zagier for the principal stratum ${\mathcal{H}}(1^{2g-2})$. They use and develop quasimodularity properties of a new all genera generating function for volumes.
3 Conjectural Universality of the Siegel–Veech Constant for Strata of Abelian Differentials of Large Genus
Main Conjecture 2.
For all nonhyperelliptic connected components ${\mathcal{H}}$ of all strata ${\mathcal{H}}(m)$ of Abelian differentials, where $m\in\Pi_{2g-2}$, one has
| $\displaystyle\lim_{g\to\infty}c_{\mathit{area}}({\mathcal{H}})=\frac{1}{2}\,.$ |
Conditional Corollary 1.
Applying the formula from [[Eskin et al.2014]] for the sum of the Lyapunov exponents of the Hodge bundle over the Teichmüller geodesic flow in any nonhyperelliptic connected component of a stratum ${\mathcal{H}}_{1}(m)$ of Abelian differentials we get
| $\lambda_{1}+\dots+\lambda_{g}\ =\ \cfrac{1}{12}\cdot\sum_{m_{i}\in m}\cfrac{m_ {i}(m_{i}+2)}{m_{i}+1}\ +\ \frac{\pi^{2}}{6}+\epsilon_{3}(m)\,,$ | (5) |
where $\lim_{g\to+\infty}\max_{m\in\Pi_{2g-2}}|\epsilon_{3}(m)|\to 0$.
Recall that the original definition of the Siegel–Veech constant comes from counting of closed geodesics. Regular simple closed geodesics on translation surfaces appear in families; every such family fills a maximal flat cylinder having at least one conical singularity on each of the two boundary components. Consider a translation surface of unit area, and let $N_{\mathit{area}}(S,L)$ be the weighted number of regular simple closed geodesics of length at most $L$, where the weight is the area of the associated maximal flat cylinder. Morally, we pretend that the geodesic is thick, and the weight measures its thickness. By the result of [Eskin and Masur2001], for almost all flat surfaces $S$ of unit area in any connected component ${\mathcal{H}}$ of any stratum of Abelian differentials, the weighted number $N_{\mathit{area}}(S,L)$ of regular simple closed geodesics has quadratic asymptotics
| $\displaystyle N_{\mathit{area}}(S,L)=c_{\mathit{area}}({\mathcal{H}})\cdot\pi L ^{2}+o(L^{2})\ \text{ as }L\to+\infty\,.$ |
Morally, Conjecture 2 claims that for a random translation surface of sufficiently large genus, the asymptotics of $N_{\mathit{area}}(S,L)$ is, basically, universal no matter what is the genus and what are the number and types of conical singularities of $S$.
Remark 4.
Due to a misunderstanding in the normalization, the conjectural value of $c_{\mathit{area}}$ indicated in [Chen2013] differs from the actual one by a constant factor.
Remark 5.
The hyperelliptic connected components excluded in the statements above exhibit completely different behavior [see [Eskin et al.2014]]:
| $\displaystyle c_{\mathit{area}}({\mathcal{H}}^{hyp}_{1}(2g-2))$ | $\displaystyle=\cfrac{(2g+1)g}{\pi^{2}(2g-1)}$ | ||
| $\displaystyle c_{\mathit{area}}({\mathcal{H}}^{hyp}_{1}(g-1,g-1))$ | $\displaystyle=\cfrac{(2g+1)(g+1)}{\pi^{2}(2g)}\,.$ |
3.1 Numerical Evidence
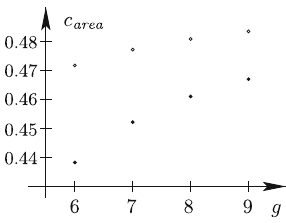
There are two sources of strong numerical evidence supporting the above conjecture. On the one hand we have exact values of $c_{\mathit{area}}({\mathcal{H}})$ for all connected components of all strata up to genus $g=9$. For this range of genera we have $c_{\mathit{area}}({\mathcal{H}})<\frac{1}{2}$ for all non hyperelliptic components of all strata. The maximal value of $c_{\mathit{area}}$ (closest to $\frac{1}{2}$) in this range of genera is attained for the principal stratum; the minimal value—for the component ${\mathcal{H}}^{odd}(2g-2)$, and both are already close to $\frac{1}{2}$, see Fig. 2.
Numerical evidence which covers strata of larger genera comes from numerical simulations for the sums of the Lyapunov exponents. For those strata where we have exact values of $c_{\mathit{area}}$, these simulations give up to five digits of precision, which gives a hope that they are sufficiently reliable in higher genera. Also, from [Eskin et al.2014] we know the exact value of $c_{\mathit{area}}({\mathcal{H}}^{hyp})$ for all genera, and it matches the numerical simulations based on evaluation of Lyapunov exponents. These kind of numerical simulations do not seem to be sensitive to a particular stratum.
3.2 State of the Art
The Main Conjecture 2 was recently proved by Chen et al. for the principal stratum ${\mathcal{H}}(1,\dots,1)$. The proof is also based on quasimodularity properties of a new generating function which the authors elaborate for $c_{\mathit{area}}$. The method is applicable to strata (3) as $g\to+\infty$.
We have an alternative conditional straightforward proof of the Main Conjecture 2 for the principal stratum ${\mathcal{H}}(1,\dots,1)$ relying on its strong version (2) proved in Chen et al. and on the original formula from [Eskin et al.2003] for $c_{\mathit{area}}$ in terms of the polynomial in volumes. The same method works for strata (3) as $g\to+\infty$ as soon as the Main Conjecture is proved in the strong form (2) for the initial stratum ${\mathcal{H}}(m(g))$ and for all analogous strata obtained by replacing any subcollection of $m_{i}$ by all possible partitions of $m_{i}-1$.
Acknowledgements
We are grateful MPIM in Bonn for constant hospitality along many years of development of this project. We thank D. Chen, M. Möller and D. Zagier for their interest to the conjectures and for important conversations. Research of Alex Eskin is partially supported by NSF Grant. Research of Anton Zorich is partially supported by IUF and by ANR.References
- [Athreya et al.2012] Athreya, J., Eskin, A., Zorich,A.: Right-angled billiards and volumes of moduli spaces of quadratic differentials on ${\mathbb{C}}{\rm P}^{1}$, (2012), pp. 1–55,
- [Chen2013] Chen, D.: Covers of the projective line and the moduli space of quadratic differentials. Geom Dedicata 163, 105–125 (2013)
- [Chen et al.0000] Chen, D., Möller, M., Zagier, D.: Work in progress
- [Eskin et al.2014] Eskin, A., Kontsevich, M., Zorich, A.: Sum of Lyapunov exponents of the Hodge bundle with respect to the Teichmüller geodesic flow. Publications de l’IHES 120(1), 207–333 (2014)
- [Eskin and Masur2001] Eskin, A., Masur, H.: Asymptotic formulas on flat surfaces. Ergod. Theory Dyn. Syst. 21(2), 443–478 (2001)
- [Eskin et al.2003] Eskin, A., Masur, H., Zorich, A.: Moduli spaces of Abelian differentials: the principal boundary, counting problems, and the Siegel–Veech constants. Publications de l’IHES 97(1), 61–179 (2003)
- [Eskin and Okounkov2001] Eskin, A., Okounkov, A.: Asymptotics of number of branched coverings of a torus and volumes of moduli spaces of holomorphic differentials. Invent. Math. 145(1), 59–104 (2001)
- [Kontsevich and Zorich2003] Kontsevich, M., Zorich, A.: Connected components of the moduli spaces of Abelian differentials with prescribed singularities. Invent. Math. 153(3), 631–678 (2003)
- [Masur1982] Masur, H.: Interval exchange transformations and measured foliations. Ann. Math. 115, 169–200 (1982)
- [Masur and Tabachnikov2002] Masur, H., Tabachnikov, S.: Rational billiards and flat structures. In: Hasselblatt, B., Katok, A. (eds.) Handbook of dynamical systems, vol. 1A, pp. 1015–1089. Elsevier, Amsterdam (2002)
- [Veech1982] Veech, W.: Gauss measures for transformations on the space of interval exchange maps. Ann. Math. 115, 201–242 (1982)
- [Wright2015] Wright, A.: Translation surfaces and their orbit closures: an introduction for a broad audience. EMS Surv. Math. Sci 2(1), 63–108 (2015)
- [Wright2016] Wright, A.: From rational billiards to dynamics on moduli spaces. Bull. AMS 53(1), 41–56 (2016)
- [Zorich2006] Zorich, A.: Flat surfaces. In: Julia, B., Vanhove, P. (eds.) Frontiers in Number Theory, Physics and Geometry. On Random Matrices, Zeta Functions and Dynamical systems; Ecole de physique des Houches, France, vol. 1, pp. 439–586. Springer, Berlin (2006)