Generalizations of Tucker–Fan–Shashkin Lemmas
School of Mathematical and Statistical Sciences
University of Texas Rio Grande Valley,
One West University Boulevard
Brownsville TX 78520 USA
oleg.musin@utrgv.edu
Abstract
Tucker and Ky Fan’s lemma are combinatorial analogs of the Borsuk–Ulam theorem (BUT). In 1996, Yu. A. Shashkin proved a version of Fan’s lemma, which is a combinatorial analog of the odd mapping theorem (OMT). We consider generalizations of these lemmas for BUT–manifolds, i.e. for manifolds that satisfy BUT. Proofs rely on a generalization of the OMT and on a lemma about the doubling of manifolds with boundaries that are BUT–manifolds.
Keywords
1 Tucker’s, Fan’s and Shashkin’s Lemmas
Throughout this paper the symbol ${\mathbb{R}}^{d}$ denotes the Euclidean space of dimension $d$. We denote by ${\mathbb{B}}^{d}$ the $d$-dimensional unit ball and by ${\mathbb{S}}^{d}$ the $d$-dimensional unit sphere. If we consider ${\mathbb{S}}^{d}$ as the set of unit vectors $x$ in ${\mathbb{R}}^{d+1}$, then points $x$ and $-x$ are called antipodal and the symmetry given by the mapping $x\to-x$ is called the antipodality on ${\mathbb{S}}^{d}$.
1.1 Tucker and Fan’s Lemma
Let $T$ be a triangulation of the $d$-dimensional ball ${\mathbb{B}}^{d}$. We call $T$ antipodally symmetric on the boundary if the set of simplices of $T$ contained in the boundary of ${\mathbb{B}}^{d}={\mathbb{S}}^{d-1}$ is an antipodally symmetric triangulation of ${\mathbb{S}}^{d-1}$; that is if $s\subset{\mathbb{S}}^{d-1}$ is a simplex of $T$, then $-s$ is also a simplex of $T$.
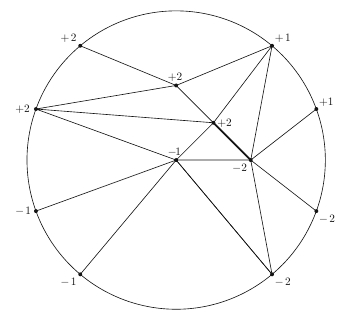
Tucker’s Lemma [Tucker1945] Let $T$ be a triangulation of ${\mathbb{B}}^{d}$ that is antipodally symmetric on the boundary. Let
| $\displaystyle L:V(T)\to\{+1,-1,+2,-2,\ldots,+d,-d\}$ |
be a labelling of the vertices of $T$ that is antipodal (i. e. $L(-v)=-L(v)$) for every vertex $v$ on the boundary. Then there exists an edge in $T$ that is complementary, i.e., its two vertices are labelled by opposite numbers.
(In Fig. 1 is given an illustration of Tucker’s lemma.)
There is also a version of Tucker’s lemma for spheres:
Spherical Tucker’s Lemma Let $T$ be a centrally symmetric triangulation of the sphere ${\mathbb{S}}^{d}$. Let
| $\displaystyle L:V(T)\to\{+1,-1,+2,-2,\ldots,+d,-d\}$ |
be an antipodal labelling. Then there exists a complementary edge.
Tucker’s lemma was extended by [Fan1952]:
Ky Fan’s Lemma Let $T$ be a centrally symmetric triangulation of the sphere ${\mathbb{S}}^{d}$. Suppose that each vertex $v$ of $T$ is assigned a label $L(v)$ from $\{\pm 1,\pm 2,\ldots,\pm n\}$ in such a way that $L(-v)=-L(v)$. Suppose this labelling does not have complementary edges. Then there are an odd number of $d$-simplices of $T$ whose labels are of the form $\{k_{0},-k_{1},k_{2},\ldots,(-1)^{d}k_{d}\}$, where $1\leq k_{0}<k_{1}<\cdots<k_{d}\leq n$. In particular, $n\geq d+1$.
1.2 Shashkin’s Lemma
In the 1990s, Yu. A. Shashkin published several works related to discrete versions of classic fixed point theorems ([Shashkin1991]; [Shashkin1994]; [Shashkin1996a]; [Shashkin1996b]; [Shashkin1999]). In [Shashkin1996b] he proved the following theorem:
Shashkin’s Lemma Let $T$ be a triangulation of a planar polygon that is antipodally symmetric on the boundary. Let
| $\displaystyle L:V(T)\to\{+1,-1,+2,-2,+3,-3\}$ |
be a labelling of the vertices of $T$ that satisfies $L(-v)=-L(v)$ for every vertex $v$ on the boundary. Suppose that this labelling does not have complementary edges. Then for any numbers $a,b,c$, where $|a|=1,\;|b|=2,\;|c|=3$, the total number of triangles in $T$ with labels $(a,b,c)$ and $(-a,-b,-c)$ is odd.
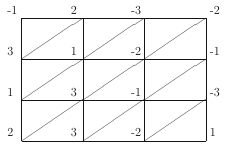
Remark.
In other words, Shashkin proved that if $(a,b,c)=(1,2,3),\,(1,-2,3),{}(1,2,-3)$ and $(1,-2,-3)$, then the number of triangles with labels $(a,b,c)$ or $(-a,-b,-c)$ is odd. Denote this number by ${\rm SN}(a,b,c)$. Then in Fig. 2 we have
| $\displaystyle{\rm SN}(1,2,3)=3,\;{\rm SN}(1,-2,3)=1,\;{\rm SN}(1,2,-3)=3,\;{ \rm SN}(1,-2,-3)=3.$ |
Note that this result was published only in Russian and only for two–dimensional case. Moreover, Shashkin attributes this theorem to [Fan1952].
Actually, Shashkin’s lemma can be derived from Ky Fan’s lemma for $n=d+1$. However. Shashkin’s proof is different and relies on the odd mapping theorem (OMT). In fact, this lemma is a discrete version of the OMT. That is why we distinguish this result as Shashkin’s lemma.
The following is a spherical version of Shashkin’s lemma.
Spherical Shashkin’s Lemma Let $T$ be a centrally symmetric triangulation of ${\mathbb{S}}^{d}$. Let
| $\displaystyle L:V(T)\to\Pi_{d+1}:=\{+1,-1,+2,-2,\ldots,+(d+1),-(d+1)\}$ |
be an antipodal labelling of $T$. Suppose that this labelling does not have complementary edges. Then for any set of labels $\Lambda:=\{\ell_{1},\ell_{2},\ldots,\ell_{d+1}\}\subset\Pi_{d+1}$ with $|\ell_{i}|=i$ for all $i$, the number of $d$–simplices in $T$ that are labelled by $\Lambda$ is odd.
1.3 Main Results
In [Musin2012] we invented BUT (Borsuk–Ulam Type) – manifolds. Theorems 3.1–3.4 in this paper extend Tucker’s and Shashkin’s lemmas for BUT–manifolds. Namely, Theorem 3.1 and Theorem 3.2 are extensions of the spherical Tucker and Shahskin lemmas, where ${\mathbb{S}}^{d}$ is substituted by a BUT–manifold. Theorems 3.3 and 3.4 are extensions of the original Tucker and Shashkin lemmas, where ${\mathbb{B}}^{d}$ is substituted by a manifold $M$ with boundary $\partial M$ that is a BUT–manifold.
Our proof of Theorem 3.2 is relies on a generalization of the odd mapping theorem for BUT–manifolds:
Theorem 2.1.
Let $(M_{1},A_{1})$ and $(M_{2},A_{2})$ be BUT–manifolds. Then any odd continuous mapping $f:M_{1}\to M_{2}$ has odd degree.
Theorems 3.3 and 3.4 follow from Theorems 3.1 and 3.2 by using Lemma 3.1, which is about the doubling of manifolds with boundaries that are BUT–manifolds.
In Section 4 we extend for BUT–manifolds Shaskin’s proof of two Tucker’s theorems about covering families from [Tucker1945]. Actually, these theorems are corollaries of Theorem 3.2.
2 The Odd Mapping Theorem
We say that a mapping $f:{\mathbb{S}}^{d}\to{\mathbb{S}}^{d}$ is odd or antipodal if $f(-x)=-f(x)$ for all $x\in{\mathbb{S}}^{d}$. If $f$ is a continuous mapping, then $\deg{f}$ (the degree of $f$) is well defined.
Let $f:M_{1}\to M_{2}$ be a continuous map between two closed manifolds $M_{1}$ and $M_{2}$ of the same dimension. The degree is a number that represents the amount of times that the domain manifold wraps around the range manifold under the mapping. Then $\operatorname{deg_{2}}2(f)$ (the degree modulo 2) is 1 if this number is odd and 0 otherwise. It is well known that $\operatorname{deg_{2}}2(f)$ of a continuous map $f$ is a homotopy invariant [see ([Milnor1969])].
The classical odd mapping theorem states that
Every continuous odd mapping $f:{\mathbb{S}}^{d}\to{\mathbb{S}}^{d}$ has odd degree.
[Shashkin1996b] (see also [[Matoušek2003], Proposition 2.4.1]) gives a proof of this theorem for simplicial mappings $f:{\mathbb{S}}^{d}\to{\mathbb{S}}^{d}$. [Conner and Floyd1960] considered Theorem 2.1 for a wide class of spaces. Here we extend the odd mapping theorem for BUT–manifolds. In our paper [Musin2012], we extended the Borsuk–Ulam theorem for manifolds.
Let $M$ be a connected compact PL (piece-wise linear) $d$-dimensional manifold without boundary with a free simplicial involution $A:M\to M$, i. e. $A^{2}(x)=A(A(x))=x$ and $A(x)\neq x$. We say that a pair $(M,A)$ is a BUT (Borsuk-Ulam Type) manifold if for any continuous $g:M\to{\mathbb{R}}^{d}$ there is a point $x\in M$ such that $g(A(x))=g(x)$. Equivalently, if a continuous map $f:M\to{\mathbb{R}}^{d}$ is antipodal, i.e. $f(A(x))=-f(x)$, then the set of zeros $Z_{f}:=f^{-1}(0)$ is not empty.
In [Musin2012], we found several equivalent necessary and sufficient conditions for manifolds to be BUT. In particular,
$M$ is a $d$–dimensional BUT–manifold if and only if $M$ admits an antipodal continuous transversal to zeros mapping $h:M\to{\mathbb{R}}^{d}$ with $|Z_{h}|=2\;\;(\mathop{{\rm mod}}4)$.
A continuous mapping $h:M\to{\mathbb{R}}^{d}$ is called transversal to zero if there is an open set $U$ in ${\mathbb{R}}^{d}$ such that $U$ contains 0, $U$ is homeomorphic to the open $d$-ball and $h^{-1}(U)$ consists of a finite number open sets in $M$ that are homeomorphic to open $d$-balls.
The class of BUT–manifolds is sufficiently large. It is clear that $({\mathbb{S}}^{d},A)$ with $A(x)=-x$ is a BUT-manifold. Suppose that $M$ can be represented as a connected sum $N\#N$, where $N$ is a closed PL manifold. Then $M$ admits a free involution. Indeed, $M$ can be “centrally symmetrically” embedded to ${\mathbb{R}}^{k}$, for some $k$, and the antipodal symmetry $x\to-x$ in ${\mathbb{R}}^{k}$ implies a free involution $A:M\to M$ [[Musin2012], Corollary 1]. For instance, orientable two-dimensional manifolds $M^{2}_{g}$ with even genus $g$ and non-orientable manifolds $P^{2}_{m}$ with even $m$, where $m$ is the number of Möbius bands, are BUT-manifolds.
Let $M_{i},\;i=1,2$, be a manifold with a free involution $A_{i}$. We say that a mapping $f:M_{1}\to M_{2}$ is antipodal (or odd, or equivariant) if $f(A_{1}(x))=A_{2}(f(x))$ for all $x\in M_{1}$.
Theorem 2.1.
Let $(M_{1},A_{1})$ and $(M_{2},A_{2})$ be $d$-dimensional BUT–manifolds. Then any odd continuous mapping $f:M_{1}\to M_{2}$ has odd degree.
Proof.
Since $(M_{2},A_{2})$ is BUT, there is a continuous antipodal transversal to zeros mapping $g:M_{2}\to{\mathbb{R}}^{d}$ with $|Z_{g}|=4m_{2}+2$ [[Musin2012], Theorem 2].
Let $h:=g\circ f$. Then $h:M_{1}\to{\mathbb{R}}^{d}$ is continuous and antipodal. Since the degree of a mapping is a homotopy invariant, without loss of generality we may assume that $h$ is a transversal to zero mapping (see [Musin2012], [Lemma 3]). Therefore $|Z_{h}|=4m_{1}+2$. On the other hand,
| $\displaystyle|Z_{h}|=\sum\limits_{x\in Z_{g}}{|f^{-1}(x)|}.$ |
Then
| $\displaystyle 2m_{1}+1=(2m_{2}+1)\operatorname{deg_{2}}2{f}\;\;(\mathop{{\rm mod }}2).$ |
Thus, the degree of ${f}$ is odd. $\square$
3 Tucker’s and Shashkin’s Lemmas for BUT–Manifolds
In our papers [Musin2012]; [Musin2015], [Musin and Volovikov2015] are considered extensions of Tucker’s lemma. Here we consider generalizations of Tucker’s and Shashkin’s lemmas for manifolds with and without boundaries.
Let $T$ be an antipodally symmetric (or antipodal) triangulation of a BUT–manifold $(M,A)$. This means that $A:T\to T$ sends simplices to simplices. Denote by $\Pi_{n}$ the set of labels $\{+1,-1,+2,-2,\ldots,+n,-n\}$ and let $L:V(T)\to\Pi_{n}$ be a labeling of $T$. We say that this labelling is antipodal if $L(A(v))=-L(v)$. An edge $uv$ in $T$ is called complementary if $L(u)=-L(v)$.
Theorem 3.1.
([Musin2015], Theorem 4.1) Let $(M,A)$ be a $d$-dimensional BUT–manifold. Let $T$ be an antipodal triangulation of $M$. Then for any antipodal labelling $L:V(T)\to\Pi_{d}$ there exists a complementary edge.
Any antipodal labelling $L:V(T)\to\Pi_{n}$ of an antipodally symmetric triangulation $T$ of $M$ defines a simplicial map $f_{L}:T\to{\mathbb{R}}^{n}$. Let $\{e_{1},-e_{1},e_{2},-e_{2},\ldots,e_{n},-e_{n}\}$ be the standard orthonormal basis in ${\mathbb{R}}^{n}$. For $v\in V(T)$, set $f_{L}(v):=e_{i}$ if $L(v)=i$ and $f_{L}(v):=-e_{i}$ if $L(v)=-i$. Since $f_{L}$ is defined on $V(T)$, it defines a simplicial mapping $f_{L}:T\to{\mathbb{R}}^{n}$ (see details in [[Matoušek2003], Sect. 2.3].)
The following theorem is a version of Shashkin’s lemma for manifolds without boundary.
Theorem 3.2.
Let $(M,A)$ be a $d$-dimensional BUT–manifold. Let $T$ be an antipodally symmetric triangulation of $M$. Let $L:V(T)\to\Pi_{d+1}$ be an antipodal labelling of $T$. Suppose that this labelling does not have complementary edges. Then for any set of labels $\Lambda:=\{\ell_{1},\ell_{2},\ldots,\ell_{d+1}\}\subset\Pi_{d+1}$ with $|\ell_{i}|=i$ for all $i$, the number of $d$–simplices in $T$ that are labelled by $\Lambda$ is odd.
Proof.
Since $L$ has no complimentary edges, $f_{L}:T\to{\mathbb{R}}^{d+1}$ is an antipodal mapping of $M$ to the boundary of the crosspolytope $C^{d+1}$ that is the convex hull ${\rm conv}{\{e_{1},-e_{1},\ldots,e_{d+1},-e_{d+1}\}}.$ Note that $\partial C^{d+1}$ is a simplicial sphere ${\mathbb{S}}^{d}$, which is a BUT-manifold. Therefore, Theorem 2.2 implies that the number of preimages of the simplex in $\partial C^{d+1}$ with indexes from $\Lambda$ is odd. It completes the proof. $\square$
Remark.
Theorem 3.1 can be proved using the same arguments. Indeed, suppose that $L:V(T)\to\Pi_{d}$ has no complementary edges. Then $f_{L}$ sends $M$ to $\partial C^{d}$. Since $\dim{\partial C^{d}}=d-1$, $\deg{f_{L}}=0$. This contradicts Theorem 2.1.
Now we extend Tucker’s and Shashkin’s lemmas for the case when $M$ is a manifold with boundary that is a BUT–manifold. But first, prove that there exists a “double” of $M$ that is a BUT-manifold.
Lemma 3.1.
Let $M$ be a compact PL manifold with boundary $\partial M$. Suppose $(\partial M,A)$ is a BUT–manifold. Then there is a BUT–manifold $(\tilde{M},\tilde{A})$ and a submanifold $N$ in $\tilde{M}$ such that $N\simeq M$, $\tilde{A}|_{\partial N}\simeq A$, $(N{\setminus}\partial N)\cap\tilde{A}(N{\setminus}\partial N)=\emptyset$ and
| $\displaystyle\tilde{M}\simeq(N{\setminus}\partial N)\cup\partial N\cup\tilde{A }(N{\setminus}\partial N).$ |
Proof.
-
1.
First we prove the following statement: Let $X$ be a finite simplicial complex. Let $Y$ be a subcomplex of $X$ with a free involution $A:Y\to Y$ . Then there is a simplicial embedding $F$ of $X$ into ${\mathbb{R}}^{q}_{+}:=\{(x_{1},\ldots,x_{q})\in{\mathbb{R}}^{q}:x_{1}\geq 0\}$ , where $q$ is sufficiently large, such that $Y$ is centrally symmetrically embedded in ${\mathbb{R}}^{q}$ , i.e. $F(A(y))=-F(y)$ for all $y\in Y$ , and $X{\setminus}Y$ is mapped into the interior of ${\mathbb{R}}^{q}_{+}$ .
Indeed, let $v_{1},v_{-1},\ldots,v_{m},v_{-m}$ denote vertices of $Y$ such that $A(v_{k})=v_{-k}$ . Let $\{v_{m+1},\ldots,v_{n}\}$ be the set of vertices of $X{\setminus}Y$ .
Denote by $C^{n}$ the $n$ –dimensional crosspolytope that is the boundary of convex hull
$\displaystyle{\rm conv}{\{e_{1},-e_{1},\ldots,e_{n},-e_{n}\}}$ of the vectors of the standard orthonormal basis and their negatives.
Now define an embedding $F:X\to C^{n}$ . Let $F(v_{k}):=e_{k}$ , $F(v_{-k}):=e_{-k}$ , where $1\leq k\leq m$ , $F(v_{k}):=e_{k}$ , and $k=m+1,\ldots,n$ . Since $F$ is defined for all of the vertices of $X$ , it uniquely defines a simplicial (piecewise linear) mapping $F:X\to C^{n}\subset{\mathbb{R}}^{n}$ . Then
$\displaystyle F(Y)\subset C^{m}\subset{\mathbb{R}}^{m}=\{(x_{1},\ldots,x_{n}) \in{\mathbb{R}}^{n}:x_{i}=0,\;i=m+1,\ldots,n\},$ $F(A(y))=-F(y)$ for all $y\in Y$ and
$\displaystyle F(X{\setminus}Y)\subset{\mathbb{R}}^{n-1}_{+}:=\{(x_{1},\ldots,x _{n})\in{\mathbb{R}}^{n}:x_{m+1}+\cdots+x_{n}>0\},$ as required.
-
2.
Let $X=M$ and $Y=\partial M$ . Then it follows from 1 that there is an embedding $F:M\to{\mathbb{R}}^{q}_{+}$ with $F(\partial M)\subset{\mathbb{R}}^{q}$ and $F(A(y))=-F(y)$ for all $y\in\partial M$ , where $q=n-1$ . Let
$\displaystyle\tilde{M}$ $\displaystyle:=$ $\displaystyle F(M)\cup(-F(M))\subset{\mathbb{R}}^{q+1}={\mathbb{R}}^{q}_{+} \cup(-{\mathbb{R}}^{q}_{+})\;\mbox{ and }$ $\displaystyle\tilde{A}(x)$ $\displaystyle:=$ $\displaystyle-x\mbox{ for all }x\in\tilde{M}.$ It is clear that $\tilde{M}\simeq(N{\setminus}\partial N)\cup\partial N\cup\tilde{A}(N{\setminus }\partial N),$ where $N:=F(M).$
-
3.
Let us prove that $(\tilde{M},\tilde{A})$ is BUT. Indeed, since $(\partial M,A)$ is BUT, there is a continuous antipodal transversal to zeros mapping $g:\partial M\simeq\partial N\to{\mathbb{R}}^{d-1}$ with $|Z_{g}|=4m+2$ , where $d:=\dim{M}.$ We extend this mapping to $h:\tilde{M}\to{\mathbb{R}}^{d}$ with $h|_{\partial N}=g$ and $|Z_{h}|=|Z_{g}|=4m+2$ .
Let $v=(x_{1},\ldots,x_{n})\in{\mathbb{R}}^{n}$ be a vertex of $\tilde{M}$. If $v\in\partial N$, then put
| $\displaystyle h(v):=(g(v),0)\in{\mathbb{R}}^{d}.$ |
For $v\in\tilde{M}{\setminus}\partial N$ define
| $\displaystyle h(v):=(0,\ldots,0,x_{m+1}+\cdots+x_{n})\in{\mathbb{R}}^{d}.$ |
Then $h:\tilde{M}\to{\mathbb{R}}^{d}$ is an antipodal transversal to
zeros mapping and $h^{-1}(0)=g^{-1}(0)$.
$\square$
Theorem 3.3.
Let $M$ be a $d$–dimensional compact PL manifold with boundary $\partial M$. Suppose $(\partial M,A)$ is a BUT–manifold. Let $T$ be a triangulation of $M$ that antipodally symmetric on $\partial M$. Let $L:V(T)\to\Pi_{d}$ be a labelling of $T$ that is antipodal on the boundary. Then there is a complementary edge in $T$.
Theorem 3.4.
Let $M$ be a $d$–dimensional compact PL manifold with boundary $\partial M$. Suppose $(\partial M,A)$ is a BUT–manifold. Let $T$ be a triangulation of $M$ that antipodally symmetric on $\partial M$. Let $L:V(T)\to\Pi_{d+1}$ be a labelling of $T$ that is antipodal on the boundary and has no complementary edges. Then for any set of labels $\Lambda:=\{\ell_{1},\ell_{2},\ldots,\ell_{d+1}\}\subset\Pi_{d+1}$ with $|\ell_{i}|=i$ for all $i$, the number of $d$–simplices in $T$ that are labelled by $\Lambda$ or $(-\Lambda)$ is odd.
Proof.
By Lemma 3.1 there is a BUT–manifold $(\tilde{M},\tilde{A})$ that is the double of $M$. We can extend $T$ and $L$ from $M$ to an antipodal triangulation $\tilde{T}:=T\cup\tilde{A}(T)$ of $\tilde{M}$ and an antipodal labelling $\tilde{L}:V(\tilde{T})\to\Pi_{n}$, where $n=d$ in Theorem 3.3 and $n=d+1$ in Theorem 3.4, such that $\tilde{L}|_{T}=L$.
Thus, for the case $n=d$ Theorem 3.3 follows from Theorem 3.1 and for $n=d+1$ Theorem 3.2 yields Theorem 3.4. $\square$
4 Shashkin’s Proof of Tucker’s Theorems
In this section we consider two Tucker’s theorems about covering families. Note that [Tucker1945] obtained these theorem only for ${\mathbb{S}}^{2}$. [Bacon1966] proved that statements in Theorems 4.1 and 4.2 are equivalent to the Borsuk–Ulam theorem for normal topological spaces $X$ with free continuous involutions $A:X\to X$. [See also Theorem 2.1 in our paper ([Musin and Volovikov2015])]. Actually, these theorems can be proved from properties of Schwarz’s genus ([Svarc1966]) or Yang’s cohomological index ([Karasev2009]; [Musin and Volovikov2015]).
For the two–dimensional case in the book [Shashkin1999] Shashkin derives Tucker’s theorems from his lemma. Here we extend his proof for BUT–manifolds of all dimensions.
Theorem 4.1.
Let $(M,A)$ be a $d$-dimensional BUT–manifold. Consider a family of closed sets $\{B_{i},B_{-i}\},\,i=1,\ldots,d+1$, where $B_{-i}:=A(B_{i})$, is such that $B_{i}\cap B_{-i}=\emptyset$ for all $i$. If this family covers $M$, then for any set of indices $\{k_{1},k_{2},\ldots,k_{d+1}\}\subset\Pi_{d+1}$ with $|k_{i}|=i$ for all $i$, the intersection of all $B_{k_{i}}$ is not empty.
Proof.
Note that any PL manifold admits a metric. For a triangulation $T$ of $M$, the norm of $T$, denoted by $|T|$, is the diameter of the largest simplex in $T$.
Let $T_{1},T_{2},\ldots$ be a sequence of antipodal triangulations of $M$ such that $|T_{i}|\to 0$. Now for all $i$ define an antipodal labelling $L_{i}:V(T_{i})\to\Pi_{d+1}$. For every $v\in V(T_{i})\subset M$ set
| $\displaystyle L_{i}(v):=\ell,\quad\mbox{where}\,v\in B_{\ell}\mbox{ and }|\ell |=\min{\{|k|:v\in B_{k}\}}.$ |
Then $L_{i}$ satisfies the assumptions in Theorem 3.2 and $T_{i}$ contains a simplex $s_{i}$ with labels $\{k_{1},k_{2},\ldots,k_{d+1}\}\subset\Pi_{d+1}$.
Since $M$ is compact and $|s_{i}|\to 0$, the sequence $\{s_{i}\}$ contains a converging subsequence $P$ with limit $w\in M$. Then for $s_{i}\in P$ we have $V(s_{i})\to w$.
By assumption, all $B_{k}$ are closed sets. Therefore $w\in B_{k_{j}}$ for all $j=1,\ldots,d+1$, and thus $w\in\cap_{j}{B_{k_{j}}}$. $\square$
Theorem 4.2.
Let $(M,A)$ be a $d$-dimensional BUT–manifold. Suppose that $M$ is covered by a family $\mathcal{F}$ of $d+2$ closed subsets $C_{1},\ldots,C_{d+2}$. Suppose that all $C_{i}$ have no antipodal pairs $(x,A(x))$, in other words, $C_{i}\cap A(C_{i})=\emptyset$. Let $0<k<d+2$. Then any $k$ subsets from $\mathcal{F}$ intersect and there is a point $x$ in this intersection such that $A(x)$ belongs to the intersection of the remaining $(d+2-k)$ subsets in $\mathcal{F}$.
Proof.
Without loss of generality, we can assume that $k\geq(d+2)/2$ and that the $k$ subsets from $\mathcal{F}$ are $C_{1},\ldots,C_{k}$. Therefore, we have to prove that there is $x\in M$ such that
| $\displaystyle x\in\bigcap\limits_{i=1}^{k}{C_{i}}\;\mbox{ and }\;A(x)\in \bigcap\limits_{i=k+1}^{d+2}{C_{i}}$ |
Set $C_{-i}:=A(C_{i})$. Let $m:=\lceil{d/2}\rceil,$
| $\displaystyle B_{1}:=C_{1}\cap(C_{-2}\cup\cdots\cup C_{-(m+1)}\cup C_{-(d+2)}),$ |
| $\displaystyle B_{2}:=C_{2}\cap(C_{-3}\cup\cdots\cup C_{-(m+2)}\cup C_{-(d+2)}),$ |
| $\displaystyle\vdots$ |
| $\displaystyle B_{d}:=C_{d}\cap(C_{-(d+1)}\cup C_{-1}\cup\cdots\cup C_{-(m-1)} \cup C_{-(d+2)}),$ |
| $\displaystyle B_{d+1}:=C_{d+1}\cap(C_{-1}\cup\cdots\cup C_{-m}\cup C_{-(d+2)}).$ |
If $B_{-i}:=A(B_{i})$, then
| $\displaystyle\bigcup\limits_{i=1}^{d+1}{B_{i}\cup B_{-i}}=\bigcup\limits_{i=1} ^{d+2}{C_{i}\cap(C_{1}\cup\cdots\cup C_{d+2})}=\bigcup\limits_{i=1}^{d+2}{C_{i }\cap M}=\bigcup\limits_{i=1}^{d+2}{C_{i}}=M.$ |
On the other hand, $B_{i}\subset C_{i}$ and $B_{-i}\subset C_{-i}$, hence $B_{i}\cap B_{-i}=\emptyset$. Therefore, the family of subsets $\{B_{i}\}$ satisfies the assumptions of Theorem 4.1. It follows that
| $\displaystyle Q:=B_{1}\cap\cdots\cap B_{k}\cap B_{-(k+1)}\cap\cdots\cap B_{-(d +1)}\neq\emptyset.$ |
Let $x\in Q$. Then
| $\displaystyle x\in C_{1}\cap\ldots\cap C_{k}\,\mbox{ and }\,A(x)\in C_{-(k+1)} \cap\cdots\cap C_{-(d+1)}.$ |
Since $k\geq m+1$ and $x\in B_{1}=C_{1}\cap(C_{-2}\cup\ldots\cup C_{-(m+1)}\cup C_{-(d+2)})$, we have $x\in C_{-(d+2)}$, i.e. $A(x)\in C_{d+2}$. $\square$
Corollary 4.1.
Let $(M,A)$ be a $d$-dimensional BUT–manifold. Then $M$ cannot be covered by $d+1$ closed sets, none containing a pair $(x,A(x))$ of antipodal points.
Note that the case $M={\mathbb{S}}^{d}$ was first considered by Lusternik and Schnirelmann in 1930.
Proof.
Suppose the converse, so $M$ can be covered by closed subsets $C_{1},\ldots,C_{d+1}$. Let $C_{d+2}:=C_{1}$. Then this covering satisfies the assumptions of Theorem 4.2. So there is $x$ such that
| $\displaystyle x\in\bigcap\limits_{i=1}^{d+1}{C_{i}}\;\mbox{ and }\;A(x)\in C_{ d+2},\quad\mbox{i.e.}\;(x,A(x))\in C_{1},$ |
a contradiction. $\square$
Acknowledgements
I wish to thank Frédéric Meunier for helpful discussions and comments.References
- [Bacon1966] Bacon, P.: Equivalent formulations of the Borsuk-Ulam theorem. Canad. J. Math. 18, 492–502 (1966)
- [Conner and Floyd1960] Conner, P.E., Floyd, E.E.: Fixed points free involutions and equivariant maps. Bull. Amer. Mat. Soc. 60, 416–441 (1960)
- [Fan1952] Fan, K.: A generalization of Tucker’s combinatorial lemma with topological applications. Ann. of Math. 56, 431–437 (1952)
- [Karasev2009] Karasev, R.N.: Theorems of Borsuk-Ulam type for flats and common transversals of families of convex compact sets. Sb. Math. 200, 1453–1471 (2009)
- [Matoušek2003] Matoušek, J.: Using the Borsuk-Ulam theorem. Springer-Verlag, Berlin (2003)
- [Milnor1969] Milnor, J.W.: Topology from the differentiable viewpoint. The University Press of Virginia, Charlottesville, Virginia (1969)
- [Musin2012] Musin, O.R.: Borsuk-Ulam type theorems for manifolds. Proc. Amer. Math. Soc. 140, 2551–2560 (2012)
- [Musin2015] Musin, O.R.: Extensions of Sperner and Tucker’s lemma for manifolds. J. of Combin. Theory Ser. A 132, 172–187 (2015)
- [Musin and Volovikov2015] Musin, O.R., Volovikov, A.Yu.: Borsuk-Ulam Type spaces. Mosc. Math. J. 15(4), 749–766 (2015)
- [Shashkin1991] Shashkin, Yu.A.: Fixed points. American Mathematical Society, Providence, RI (1991)
- [Shashkin1994] Shashkin, Yu.A.: Local degrees of simplicial mappings. Publ. Math. Debrecen 45, 407–413 (1994)
- [Shashkin1996a] Shashkin, Yu.A.: Remark on local degrees of simplicial mappings. Publ. Math. Debrecen 49, 301–304 (1996)
- [Shashkin1996b] Shashkin, Yu.A.: Variants of Tucker’s combinatorial lemma. Proc. IMM UrB of RAS 4, 127–132 (1996). (in Russian)
- [Shashkin1999] Shashkin, Yu.A.: Combinatorial lemmas and simplicial mappings. Ural State University Press, Yekaterinburg (1999). (in Russian)
- [Svarc1961] Švarc, A.S.: The genus of a fiber space. Trudy Moskov. Mat. Obsc. 10, 217–272 (1961)
- [Svarc1962] Švarc, A.S.: The genus of a fiber space. Trudy Moskov. Mat. Obsc. 11, 99–126 (1962)
- [Svarc1966] Švarc, A.S. (Russian), English translation in Amer. Math. Soc. Translat., II. Ser., 55, 49–140 (1966)
- [Tucker1945] Tucker, A.W.: Some topological properties of the disk and sphere. In: Proc. of the First Canadian Math. Congress, Montreal, 285–309 (1945)