Hénon maps: a list of open problems

\[ H_{a,c} (x,y) := (ay+x^2+c, a x) \]

are arguably the simplest examples. Here \(a\) and \(c\) are fixed parameters and \(x,y\) are affine coordinates The exact definition of (quadratic) Hénon maps may differ from section to section in these notes, as one might want to conjugate them by affine transformations to exploit various aspects of the original equations.× ¹ . These maps can be analyzed over the real numbers using techniques from smooth dynamical systems, or over the complex numbers and then complex analysis and geometry play crucial roles. They are amenable to generalizations, by replacing \(x^2+c\) by higher degree polynomials, or even transcendental maps, and we may consider finite composition of such maps. We may also consider them with coefficients in number fields, and look at them from the perspective of arithmetic dynamics. Many of the most recent breakthroughs were actually made by combining several techniques coming from these different fields. It was delightful to attend series of talks blending so many different ideas. Many interesting questions were raised during the conference, a fact which encouraged us to collect them in a single text.

Hénon introduced his family of maps in the real domain as a simplified model of the Poincaré section of the first return map of the Lorenz flow  [87] . In 1976, Hénon made numerical experiments for the map \(H_{\sqrt {0.3}, -1.4}\) Hénon actually considered the map \(h(x,y)=(1-1.4\cdot x^2+y\, , \, 0.3\cdot x)\) which is affinely conjugate to it.× ² and observed that an initial point of the plane either approaches a set of points known since then as the Hénon strange attractor, or diverges to infinity under iterations. The Hénon attractor has a fractal nature: it is smooth in the unstable direction and has a Cantor-like structure in the transversal direction. This led Hénon to conjecture the existence of an ergodic measure which restricts to the Lebesgue measure in the smooth direction (a.k.a. an SRB measure). In 1981, Jakobson [95] proved the existence of a set of positive Lebesgue measure of parameters \(c\) for which \(x^2+c\) displays an SRB measure. In the 90's, Benedicks and Carleson [24] reworked Jakobson's theorem and further generalized it to describe the dynamics of Hénon maps. They proved \(H_{a,c}\) display a strange attractor for \(a\) small and for a set of parameters \(c\) of positive Lebesgue measure. Benedicks-Carleson's breakthrough has been further developed by Mora-Viana [119] , Wang-Young [149] , and Takahasi [141] .

In 1996, during his inaugural lecture at Collège de France, Yoccoz proposed an alternative approach to prove the Hénon conjecture, with Sinai's positive entropy conjecture lying in the horizon. To this end, he introduced a combinatorial and topological approach, based on the notion of strong regularity, that he used to give yet another proof of Jakobson's theorem [153] . The second step of Yoccoz' program was completed more recently by Berger in [25] who generalized this notion of strong regularity, leading him in particular to an alternative proof of Benedicks-Carleson theorem.

The theory of Hénon maps in the complex domain started with the seminal work of Friedland and Milnor [81] , who used Jung's theorem to show that every polynomial automorphism of the complex affine plane is affinely conjugate to either an affine map, or a map preserving the pencil \(x=\mathrm {cst}\), or to a finite compositions of generalized Hénon maps (the latter class being usually called complex Hénon maps nowadays). In the early 90's Hubbard and his collaborators developed a topological approach to the study of Hénon maps giving description of the Fatou sets [90, 92] . Hubbard pointed out that Hénon maps appeared as natural generalizations of quadratic polynomials (by taking \(a \to 0\) in \(H_{a,c}\)), which he used with Oberste-Vorth to give topological description of Julia sets  [91] .

An important breakthrough was the introduction of pluripotential techniques to construct invariant currents by Fornæss and Sibony  [79] and by Bedford and Smillie  [17] . The latter authors, partly with Lyubich, further developed in a series of influential papers (e.g.,  [18] , [16] , [15] ) a thorough study of the ergodic properties of Hénon mappings and of their stability properties linked to hyperbolicity. These works were pursued and generalized to other invertible maps by many others including Diller, Cantat, Dujardin, Dinh and Sibony  [55] , [42] , [69] , [68] , [58] , [62] . Very recently, Bianchi and Dinh [31] made significant progress in the study of the fine statistical properties of the maximal entropy measure.

It is intriguing to see in retrospect how these seemingly simple maps have produced such an elaborate and successful theory. Note however that the results obtained so far are most complete in the case of dissipative maps (that is \(|a|<1\)), while the understanding of the conservative case (that is \(|a|=1\)) remains less developed.

In the past decade, the algebraic and arithmetic aspects of dynamical systems defined by rational maps have also been developed extensively. We refer to the survey  [23] in which one can find a large set of open problems in this emerging field. For Hénon maps defined over a number field or over a function field, Silverman [140] , and later Kawaguchi [99] , constructed a suitable height function that lead to interesting analogs of the Northcott property (see also [93] ). Hénon maps have also been the testing ground of some important conjectures in arithmetic dynamics like the Kawaguchi-Silverman conjecture on arithmetic degrees [100] , or the dynamical Manin-Mumford problem which was partially solved by Dujardin and Favre using both height and Pesin theories [73] . Deep connections exist between the arithmetic of these systems and pluripotential theoretic techniques: it is for instance possible to retrieve the equidistribution of repelling periodic orbits using a theorem on the equidistribution of points of small height by Yuan [155] .

The study of Hénon maps is still very active, as shown by the recent breakthroughs in the study of wandering domains. On the one hand, Ou  [125] has proved the absence of wandering domains for strongly dissipative doubly infinitely period-doubling renormalizable real Hénon maps. On the other hand, Berger and Biebler [27] exhibited wandering domains for complex Hénon maps in 2023 by mixing deep techniques coming from both real and complex dynamics. We also witness exciting new developments extending the already rich theory of Hénon maps to more general systems such as transcendental diffeomorphisms of the complex plane  [4] , [5] , [6] , or higher dimensional invertible rational maps, [54] , [60] , [63] , [64] , [85] , where questions arising from complex dynamics led to profound developments in complex geometry such as PB currents, density currents and superpotential theory. Several developments have been made also in the context of higher dimensional unfoldings of homoclinic tangencies with a rank one saddle point, [127, 147, 150] . We hope that gathering these questions and open problems at one place will reinforce the community and attract new generations of researchers to work on these beautiful and rich objects.

Acknowledgments The idea to collect this list of problem arose after holding a problem session at a BIRS conference which was lively chaired by M. Abate. We thank all participants of this session and the other contributors to this list to have generously shared their ideas and problems on Hénon maps. We are also grateful to Zin Arai, André de Carvalho, Sébastien Gouëzel, Stéphane Lamy, Misha Lyubich, Joseph Silverman, Liz Vivas, and the referee for their careful reading and their comments on previous versions of this manuscript.

We propose a set of questions on the dynamics of Hénon maps in the real domain, or more generally on entire diffeomorphisms of \(\mathbb {R}^2\).

2.1. Strange attractors

Attractors play an important role in the study of dynamical systems since the 60's (Lorenz attractor, Hénon strange attractor, etc.). This notion is quite flexible and can cover many different situations in which a substantial set of points (either in the topological or measurable sense) is converging to some invariant compact subset. We refer to Milnor  [113] for a discussion of various possible definitions of attractors. For instance, a measure-theoretical attractor is an invariant compact subset which attracts a set of Lebesgue positive measure and which is minimal with this property.

In the case of unimodal interval dynamics, measure-theoretical attractors can be classified into four types: cyclic, solenoidal, interval and wild (see, e.g.,  [36] ). The latter two classes are arguably the most interesting. Jakobson  [95] proved the abundance of quadratic maps displaying a stochastic interval of attractors (induced by an SRB measure). On the other hand, Bruin-Keller-Nowicki-van Strien  [39] showed the existence of a polynomial unimodal map displaying a wild attractor: an invariant Cantor set attracting Lebesgue almost every point and included in a transitive interval.

Van Strien  [145], Question 1.9 asked whether a suitable analog of wild attractors could exist for Hénon maps (of some degree). More precisely, one can ask:

Question 1.

Can we find a Hénon map which admits a wild attractor, i.e., a Cantor set which attracts a set of Lebesgue positive measure and which is strictly included in a transitive set ?

Avila and Lyubich have announced a positive answer to this problem in the quadratic Hénon family.

Returning to stochastic attractors, observe that the existence of a parameter \(c\in \mathbb {R}\) for which the quadratic map \(x \mapsto x^2+c\) displays an absolutely continuous measure is easy to ensure. It suffices to pick a parameter \(c\) such that the post-critical orbit is finite but not periodic. In fact, much more is known. Lyubich ruled out the existence of wild attractors for real quadratic maps [107] . He also showed in  [108] the following “regular or stochastic Dichotomy”: for Lebesgue almost every quadratic map, almost all orbits either converge to an attracting cycle, or they are equidistributed with respect to an absolutely continuous invariant measure with positive entropy.

In dimension \(2\), the existence of a positive measure set of parameters of Hénon maps displaying an attractor supporting an invariant SRB measure i.e., a measure whose conditional measures along unstable curves are absolutely continuous.× ³ is a fundamental result, whose proof still remains difficult and lengthy ( [24] , [25] , [141] , [149] ).

Question 2.

Is there a quick proof for the existence of SRB for some parameters of the Hénon maps?

A positive answer to this question might help finding new examples of stochastic attractors in the Hénon maps.

2.2. Non-statistical behavior

Let \(f\) be any smooth dynamical system. We say that a point \(x\) has a non-statistical behavior (or simply is non-statistical) if its sequence of empirical measures \(e_n(x):= \tfrac 1n \sum _{k=0}^{n-1} \delta _{x_n} \) is not converging. We say that \(f\) is non-statistical if there is a positive Lebesgue measure set of points with non convergent empirical measures. Ruelle  [134] asked whether non-statistical dynamics could exist persistently Ruelle used another terminology and talked about historical behavior.× ⁴ .

In polynomial dynamics, two phenomena give rise to non-statistical dynamics. The first one was discovered by Hofbauer and Keller:

  

Theorem 1 ([88]) .

There exist uncountably many \(c\in \mathbb {R}\) such that the quadratic polynomial \(P_c(x):= x^2+c\) has non-statistical dynamics. More precisely, Lebesgue almost every non-escaping point \(x\) has non-statistical behavior.

In [142] , Talebi gave a counterpart of this result for rational functions on the Riemann sphere. In these two results, the set of non-statistical points is of full measure, but of empty interior.

The second occurrence of non-statistical dynamics is related to the notion of wandering stable component that we now introduce.

Definition 1.

A stable domain of \(f\) is a connected open subset \(U\) such that

\[\lim _{n\to \infty }d(f^n(x), f^n(y))= 0\]

for all \(x,y\in U\). A stable component is a maximal stable domain. A stable component is wandering if it is not preperiodic.

Colli and Vargas [48] gave the first example of a smooth dynamical system having a wandering stable component formed by points with non-statistical behavior. In [101] , Kiriki and Soma constructed a locally dense set of such dynamics in the \(C^r\)-category with \(r<\infty \). This also occurs for polynomial maps:

[27] " class="Theorem TheoremMain" onclick="('container5')">   

Theorem 2 ( [27] ) .

There is a locally dense set of real sextic polynomials \(P(x)= x^6+ a_4 x^4 + \cdots + a_0\), for which the map \((x, y)\mapsto (P(x)-b y,x)\) displays a wandering stable component containing only points with non-statistical behavior.

The proof of this theorem actually implies the existence of a wandering Fatou component at the same parameters for its complex counterpart. This is in sharp contrast with the one-dimensional situation for which no wandering Fatou components exist by Sullivan's theorem.

Conversely, we can ask whether a counterpart of Hofbauer-Keller phenomenon appears within the Hénon family. We can formulate this question in more precise terms.

Question 3.

Do there exist \(\varepsilon >0\) and a locally dense set i.e., whose closure has non-empty interior.× ⁵ \(E\) of quadratic Hénon maps for which every point starting in some set of Lebesgue measure at least \(\varepsilon \) has non-statistical behavior?

By [142], Theorem 1.14 , this would imply the existence of a generic set of the closure of \(E\) of non-statistical dynamics.

2.3. Conservative dynamics

Let \(f\colon S \to S\) be any homeomorphism of a closed surface \(S\). An annular rotation domain for \(f\) is by definition an \(f\)-invariant open annulus that does not contain any periodic points. Such domains play an important role in conservative dynamics. The next result can be deduced from the works of [80] , [102] , [103] , [152] (Le Calvez, private communication).

Theorem 3.

Let \(S\) be a closed surface endowed with a symplectic form. Let \(f\colon S \to S\) be any symplectomorphism of class \(C^r\) with \(r\ge 1\) that contains at least one periodic point and satisfying the following conditions.

1. Any eigenvalue of any periodic point does not belong to \(\{e^{2\pi ip/q}: p/q\in \mathbb Q\}\).
2. For every hyperbolic periodic points \(P, Q\in \mathrm {Per}(f)\), \(W^s(P)\) is transverse to \(W^u(Q)\).
3. Every elliptic point \(P\in \mathrm {Per}(f)\) is surrounded by arbitrarily close KAM circles.
4. There are no annular rotation domain.

Then \(\bigcup _{P\in \mathrm {Per}(f)} W^s(P)\) is dense in \(S\).

It is natural to ask whether the third condition is superfluous. The recent result [124] suggests that this may be the case.

Question 4.

Is there a real, conservative, polynomial Hénon map with an annular rotation domain? Is there an open set of such real, conservative, polynomial Hénon maps?

An annular rotation domain is said to be trivial when the whole dynamics is conjugate to a rotation.

Question 5.

Is there an entire i.e., an analytic map which extends to a holomorphic map of \(\mathbb {C}^2\).× ⁶ symplectomorphism of \(\mathbb {R}^2\) with a non trivial annular rotation domain?

Recently, an entire map of the cylinder \(\mathbb {R}\times \mathbb {R}/\mathbb {Z}\) having a bounded rotation domain on which the dynamics is not conjugate to a rotation has been exhibited in [26] , thereby disproving a conjecture by Birkhoff [32] . The construction in [26] also gives an example of a symplectic entire automorphism of \(\mathbb {C}\times \mathbb {C}/\mathbb {Z}\) without periodic point and with a non-empty set of (Lyapunov) unstable points an orbit \((x_n)_{n\ge 0} \) is Lyapunov stable if for any \(y_0\) close enough to \(x_0\), then \(y_n\) stays close to \(x_n\) for all \(n\ge 0\).× ⁷ . Hence Question 9 may shed light on the following intriguing problem.

Problem 1.

Construct an entire symplectic automorphism of \(\mathbb {C}^2\) without periodic point and with non-empty set of (Lyapunov) unstable points with bounded orbit.

Kneading theory is a combinatorial tool to understand the dynamics of a piecewise monotone map from the interval to itself and was developed by Milnor and Thurston  [114] . Applications extend from the topological classification to the computation of the entropy, to the counting of periodic orbits, and the construction of measures of maximal entropy. We propose several problems connected to the extension of this theory to real Hénon maps and the Lozi maps \(\tH _{a,b}, L_{a,b} \colon \mathbb {R}^2 \to \mathbb {R}^2\),

\[\tH _{a,b}(x,y) = (1 + y - ax^2, bx), \quad L_{a,b}(x,y) = (1 + y - a|x|, bx),\]

respectively observe that \(\tH _{a,b}\) is affinely conjugated to \(H_{\sqrt {b},-a}\) from the introduction× ⁸ . The Lozi maps are piecewise affine map that display the same fold and bend behavior as the Hénon maps, but are usually easier to analyze technically  [76] , [116] .

In [117] , the authors developed a kneading theory for the Lozi maps \(L_{a,b}\) with \((a,b) \in \mathcal {M}\), where \(\mathcal {M} = \{ (a,b) \in \mathbb {R}^2 : b > 0, \ a\sqrt {2} - b > 2, \ 2a + b < 4 \}\) is a set of parameters for which Misiurewicz proved the existence of a strange attractor (for details see [117] and [118] ). A kneading sequence \(\bar k\) is defined as the itinerary of a turning point \(T\), where turning points are points of transversal intersections of the \(x\)-axis and the unstable manifold \(W^u\) of the fixed point \(X\) of the attractor. Any kneading sequence is a bi-infinite sequence of \(+\) and \(-\).

The kneading set \(\mathfrak {K} = \{ \bar k^n : n \in \mathbb {Z}\}\) is the set of all kneading sequences \(\bar k^n\), \(n \in \mathbb {Z}\), and every kneading sequence \(\bar k = \bar k^n\), for some \(n \in \mathbb {Z}\), has the following form:

\[\bar k = \hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} w \pm \sq \overrightarrow k_{\hspace {-.1cm} 0},\]

where \(\hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} = \dots + + +\), \(w = w_0 \dots w_m\), for some \(m \in \mathbb {N}_0\), \(\overrightarrow k_{\hspace {-.1cm} 0} = k_0 k_1 k_2 \dots \), \(w_0 = -\), \(k_0 = +\), \(w_i, k_j \in \{ -, + \}\) for \(i = 1, \dots , m\) and \(j \in \mathbb {N}\), and the little black square \(\sq \) indicates where the 0th coordinate is located. Here for \(\pm \) one can substitute any of \(+\) and \(-\).

In [117] , the authors prove that \(\mathfrak {K}\) characterizes all itineraries of all points of the attractor of \(L_{a,b}\). The proof is given in two steps. We say that an itinerary is \(W^u\)-admissible if it is realized by a point on the unstable manifold \(W^u\). We first have:

In [94] , Ishii developed formulas that can be used to obtain a relation between parameters \(a, b\), a turning point \(T = (x_T, 0)\) of the Lozi map \(L_{a,b}\), and its itinerary \(\bar k\) (that is a kneading sequence of \(L_{a,b}\)). This relation is \(p(a, b, \bar k) = x_T = q(a, b, \bar k)\), where \(p = p(a, b, \bar k)\) is given in formula [93], (4.2) and \(q = q(a, b, \bar k)\) is given in formula [93], (4.3) . Therefore, every kneading sequence \(\bar k\) gives an equation

\begin{equation} p(a, b, \bar k) = q(a, b, \bar k). \end{equation}

Numerical experiments show that if one has two kneading sequences, \(\bar k^0\) of the rightmost turning point \(T_0\) and \(\bar k^{-1}\) of the leftmost turning point \(T_{-1}\), and if these two turning points lie in the stable manifolds of some periodic points with small periods, then it is possible to calculate \(a\) and \(b\) from the corresponding two equations, implying that these two kneading sequences govern all other kneading sequences.

4.0.1. Example

Let \(\bar k^0 = \hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} \pm \sq + - - +^{\hspace {-.1cm}\infty }\) and \(\bar k^{-1} = \hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} - \pm \sq (+ -)^\infty \). The equation \(p(a, b, \bar k^0) = q(a, b, \bar k^0)\) reads

\(\seteqnumber{0}{}{1}\)

\begin{equation} a^4 - 6a^2 -4a + 4 b^2 + a^2b + (a^3 + 2a - ab)\sqrt {4 b + a^2} = 0, \end{equation}

and the equation \(p(a, b, \bar k^{-1}) = q(a, b, \bar k^{-1})\) reads

\(\seteqnumber{0}{}{2}\)

\begin{equation} \frac {4(-a^2-2b^2+2b+a \sqrt {a^2-4b})}{a-2b-\sqrt {a^2-4b}} - \left (2+a-\sqrt {a^2+4b}\right )\left (3a-\sqrt {a^2+4b}\right )=0. \end{equation}

Using the “NSolve” command of Wolfram Mathematica produces a unique solution to this system of equations in the region \(a\in [1,2]\), \(b\in [0,1]\). This solution is approximately \(a = 1.655319602968851744592, b = 0.2765071079677260998121\), see Figure 1 .

Figure 1: Graph of (2) is in orange and of (3) in green. Graph of (1) for \(\bar k = \hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} \pm \sq (+ - -)^\infty \) is in magenta and for \(\bar k = \hspace {.2cm}+^{\hspace {-.5cm}\infty }\hspace {.2cm} - \pm \sq (+ - -)^\infty \) in brown. Graph of the line \(2a + b = 4\), that is a boundary line of the Misiurewicz set, is in red.

Question 12.

Is it true that any two distinct kneading sequences determine a unique pair of parameters \((a,b)\), and in that way govern all the other kneading sequences of \(\mathfrak {K}\)?

Very recently, in [38] , the authors developed a kneading theory for the Hénon maps \(H_{a,b}\) within a set of parameters \(\mathcal {WY}\) for which Wang and Young proved the existence of a strange attractor. This set has positive measure and consist of maps which are strongly dissipative. We refer to [38] and [149] for details.

Problem 3.

Describe the set of kneading sequences \(\mathfrak {K}\) of the Hénon map \(H_{a,b}\), with \((a,b) \in \mathcal {WY}\).

Question 13.

Is it true that any two distinct kneading sequences of the Hénon map \(H_{a,b}\), with \((a,b) \in \mathcal {WY}\), determine a unique pair of parameters \((a,b)\), and in that way govern all the other kneading sequences in \(\mathfrak {K}\) of \(H_{a,b}\)?

We propose to investigate the local dynamics of some specific Hénon maps. Consider the quadratic complex Hénon map \(H_2\colon \mathbb {C}^2\to \mathbb {C}^2\) defined by

\[H_2\left (x,y\right ) = \left (y,x+y^2\right ).\]

The origin is a fixed point and \(H_2^{\circ 2}\) is tangent to the identity at the origin.

Note that \(H_2\) restricts to an orientation reversing diffeomorphism \(H_2\colon \mathbb {R}^2\to \mathbb {R}^2\). The dynamics in \(\mathbb {R}^2\) is well understood. There is an analytic map \(\phi _2\colon \mathbb {R}\to \mathbb {R}^2\) such that

\[H_2\circ \phi _2(t) = \phi _2(t+1) \ \mathrm {and} \ \phi _2(t)\sim \left (\frac {-2}{t},\frac {-2}{t}\right )\text { as } t\to +\infty .\]

The curve \(\phi _2(\mathbb {R})\) is invariant by \(H_2\) and within \(\phi _2(\mathbb {R})\), every orbit converges to the origin in \(\mathbb {R}^2\). Outside the origin and \(\phi _2(\mathbb {R})\), every orbit diverges to infinity (see Figure 2 ).

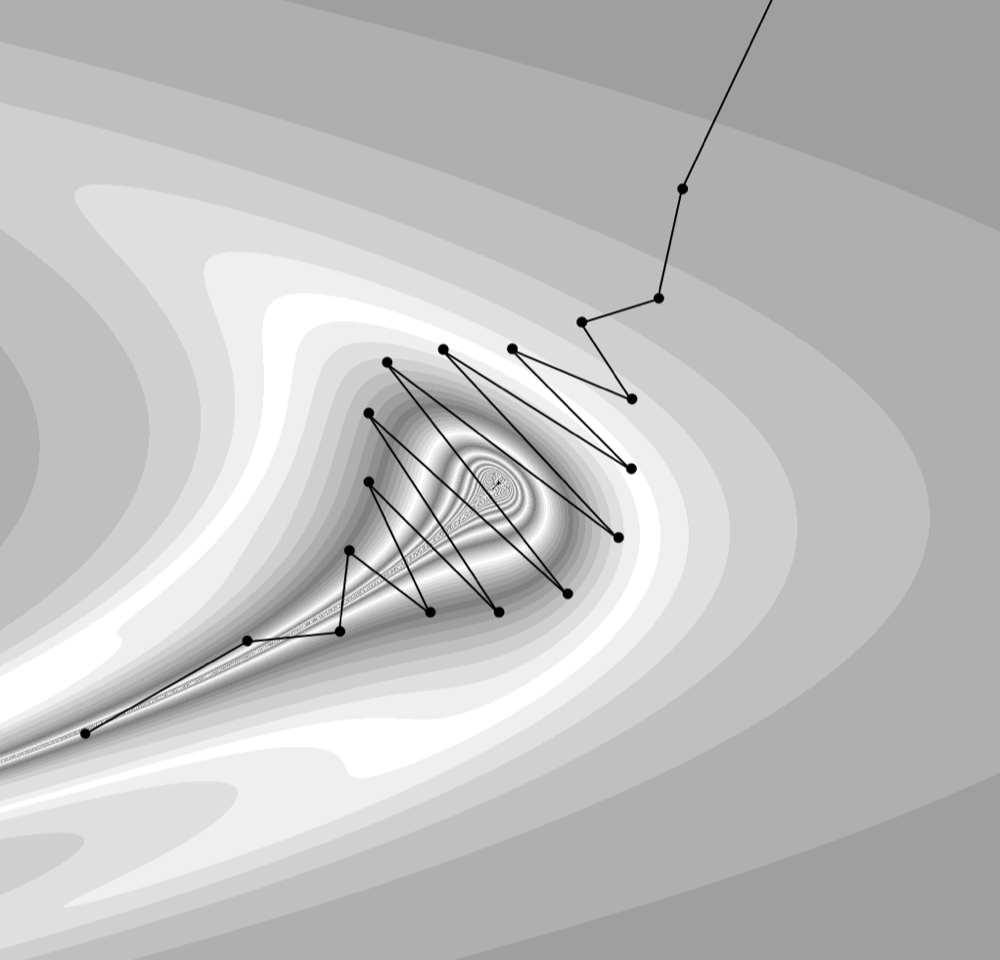
Before specifying this question, let us consider the Hénon map \(H_3\colon \mathbb {C}^2\to \mathbb {C}^2\) defined by

\[H_3\left (x,y\right ) = \left (y,x+y^3\right ).\]

This Hénon map also preserves \(\mathbb {R}^2\) and the dynamics in \(\mathbb {R}^2\) is also completely understood. There is an analytic map \(\phi _3\colon \mathbb {R}\to \mathbb {R}^2\) such that

\[H_3\circ \phi _3(t) = -\phi _3(t+1)\ \mathrm {and} \ \phi _3(t)\sim \left (\frac {1}{\sqrt {t}},\frac {-1}{\sqrt {t}}\right )\text { as } t\to +\infty .\]

The curves \(\phi _3(\mathbb {R})\) and \(-\phi _3(\mathbb {R})\) are exchanged by \(H_3\). Within those curves, every orbit converges to the origin. Outside those curves and the origin, every orbit diverges to infinity (see Figure 3 left).

Set \(\omega = e^{{\rm i}\frac {\pi }{8}}\) so that \(\omega ^9 = -\omega \) and consider the real planes \(\Pi _1\subset \mathbb {C}^2\) and \(\Pi _2\subset \mathbb {C}^2\) defined by

\[\Pi _1 = \left \{\left (\omega x,\omega ^3 y\right ) ~:~x\in \mathbb {R},~y\in \mathbb {R}\right \}\ \mathrm {and} \ \Pi _2 = \left \{\left (\omega ^3 x,\omega y\right ) ~:~x\in \mathbb {R},~y\in \mathbb {R}\right \}.\]

Observe that \(H_3\) exchanges the planes \(\Pi _1\) and \(\Pi _2\):

\[H_3\left (\omega x,\omega ^3 y\right ) = \left (\omega ^3 y, \omega (x-y^3)\right ) \ \mathrm {and} \ H_3\left (\omega ^3 x,\omega y\right ) = \left (\omega y, \omega ^3 (x+y^3)\right ).\]

The dynamics of \(H_3^{\circ 2}\colon \Pi _1\to \Pi _1\) is much more complex than that of \(H_3\colon \mathbb {R}^2\to \mathbb {R}^2\) (see Figure 3 right).

The second iterate of \(H_3\) is tangent to the identity at the origin. More precisely

\[H_3^{\circ 2}\left (x,y\right ) = \left (x,y\right ) + \left (y^3,x^3\right ) + {\mathcal O}\bigl (\|x,y\|^4\bigr ).\]

It follows that near the origin, the orbits of \(H_3^{\circ 2}\) shadow the orbits of the vector field

\[\vec {v}_3 = y^3 \partial _x + x^3\partial _y.\]

The vector field is a Hamiltonian vector field. It is tangent to the level curves of the function

\[\Phi _3= x^4-y^4.\]

Note that

\[\Phi _3\left (\begin {array}{c}\omega x \\ \omega ^3 y\end {array}\right ) = {\rm i}(x^4+y^4)\]

so that the intersection of the level curves of \(\Phi _3\) with the real plane \(\Pi _1\) are topological circles. Those topological circles are invariant by the flow of the vector field \(\vec {v}_3\). It follows from the theory of Kolmogorov-Arnold-Moser that in any neighborhood of the origin, there is a set of positive Lebesgue measure of topological circles which are invariant by \(H_3\) and on which \(H_3\) is analytically conjugate to a rotation \(\mathbb {R}/\mathbb {Z}\ni t\mapsto t+\theta \in \mathbb {R}/\mathbb {Z} \) with bounded type rotation number \(\theta \in (\mathbb {R}\smallsetminus \mathbb {Q})/\mathbb {Z}\). Those invariant circles are separated by small saddle cycles and small elliptic cycles. The analytic conjugacies extend to complex neighborhoods of \(\mathbb {R}/\mathbb {Z}\) in \(\mathbb {C}/\mathbb {Z}\). This proves that \(H_3\) has lots of Herman rings.

Coming back to our initial problem, observe that the second iterate of \(H_2\) is also tangent to the identity at the origin with

\[H_2^{\circ 2}(x,y) = (x,y) + \left (y^2,x^2\right ) + {\mathcal O}\bigl (\|x,y\|^3\bigr ).\]

It follows that near the origin, the orbits of \(H_2^{\circ 2}\) shadow the orbits of the vector field

\[\vec {v}_2 = y^2 \partial _x + x^2\partial _y.\]

The vector field is also a Hamiltonian vector field. The vector field \(\vec {v}_2\) is tangent to the level curves of the function

\[\Phi _2= x^3-y^3.\]

We can no longer apply the theory of Kolmogorov-Arnold-Moser since there is no invariant real-plane on which the level curves of \(\Phi _2\) are topological circles. However, we may wonder whether the complex dynamics of \(H_2\) exhibits KAM phenomena.

We say that \(H_2\) has small cycles if for any neighborhood \(U\) of the origin \(\boldsymbol {0}\) in \(\mathbb {C}^2\), there exists a cycle of \(H_2\) which is entirely contained in \(U\smallsetminus \{\boldsymbol {0}\}\).

We say that \(H_2\) has a Herman ring with rotation number \(\theta \in (\mathbb {R}\smallsetminus \mathbb {Q})/\mathbb {Z}\) if there exists an annulus \(V= \bigl \{z\in \mathbb {C}/\mathbb {Z}~:~{\rm Im}(z)<h\bigr \}\) with \(h>0\), a holomorphic map \(\phi \colon V\to \mathbb {C}^2\), and an integer \(n\geq 2\) such that

\[\forall z\in V,\quad H_2^{\circ n}\circ \phi (z) = \phi (z+\theta ).\]

If the answer is yes, we may consider the set \(\Theta \subset (\mathbb {R}-\mathbb {Q})/\mathbb {Z}\) of rotation numbers \(\theta \) such that \(H_2\) has a Herman ring with rotation number \(\theta \).

We believe that the answers to the previous questions are all affirmative. Regarding the following question, we do not have an opinion.

For polynomials and rational maps in dimension 1, there is a well-known list of exceptional examples whose Julia sets and dynamical properties are unexpectedly regular: Chebychev polynomials, monomial mappings and Lattès examples. They can characterized in many different ways, see e.g.,  [156] , [46] .

For generalized Hénon maps (as defined in § 6.1 ) it is expected that no such exceptional example exists, but not so many actual results in this direction are known:

• Brunella proved in [40] that a generalized Hénon map cannot preserve an algebraic foliation of \(\mathbb C^2\), i.e., a singular algebraic foliation by holomorphic curves. Here by preserving we mean that \(f\) maps leaves into leaves.
• Bedford and Kim proved in [13] , [14] that neither \(J^+\) nor \(J^-\) (see § 6.2 for a definition) can be a smooth \(C^1\) submanifold, nor a semi-analytic set.

Here we propose a few rigidity questions related to these results.

The first question is about a quantitative reinforcement of the Bedford-Kim theorem. Recall from the introduction, the definition of the standard quadratic Hénon map \(H_{a,c} (x,y) := (ay+x^2+c, a x)\), and the definition of \(K^+\) and \(J^+\) from § 6.2 .

For \((a,c)\) close to \((0, 0)\), \(H_{a,c}\) is a small perturbation of the monomial map \((x,0) \mapsto (x^2, 0)\), whose Julia set is smooth, and in this case \(J^+_{a,c}\) is a topological 3-manifold, see  [91], §7 , and  [143], §9 .

Note that \((a,c)\mapsto \dim (J^+_{a,c})\) is real analytic in the domain where \(H_{a,c}\) is hyperbolic (this was proved for one-dimensional maps by Ruelle in  [132] , and by Wolf  [151] for polynomial automorphisms). It is not clear whether the dimension of the Julia set remains real-analytic when \(H_{a,c}\) degenerates to a unimodal map, for instance in a full neighborhood of \((a,c) = (0,0)\).

Can we make Brunella's theorem local? More precisely:

We conjecture that the answer to this question is “no”. The answer is presumably easier if we assume that \(U\cap J^*\neq \emptyset \). It is also possible that if \(f\) is dissipative (i.e., \(|\det (D f)|<1\)), the assumption that \(J^-\) is foliated is stronger than the assumption that \(J^+\) is foliated (see [11], §2 ).

This would imply in particular that a generalized Hénon map cannot preserve a (transcendental) holomorphic foliation \(\mathcal F\) of \(\mathbb {C}^2\). Indeed in such a case, consider the leaf \(L\) through a saddle periodic point \(p\): \(L\) must be mapped into itself by \(f^n\), hence coincide with the stable \(W^s(p)\) or unstable \(W^u(p)\) manifolds (see again § 6.2 for a discussion of these objects); changing \(f\) to \(f^{-1}\) if necessary, we may assume that \(L = W^s(p)\), and since \(W^s(p)\) is dense in \(J^+\) it follows that \(J^+\) is a union of leaves of \(\mathcal F\).

Related results include:

• the classification of holomorphic Anosov diffeomorphisms on surfaces by Ghys [82] , in which a basic step is to prove that stable and unstable laminations are actually holomorphic foliations;
• the classification of birational maps preserving algebraic foliations by Cantat and Favre [43] ;
• the work of Pinto, Rand and others on the smooth rigidity of hyperbolic diffeomorphisms on surfaces (see e.g.,  [129] ).

If the stable lamination is holomorphic, then by holonomy the unstable slices are holomorphically equivalent. We can now forget the foliation and ask about holomorphic equivalence of stable/unstable slices.

One obvious possibility is that \(p\) and \(q\) belong to the same cycle, and that the biholomorphism is induced by the action of \(f\). We suspect that this is the only possibility.

A variant of this problem is when \(p\) and \(q\) are associated to different mappings.

Since a local unstable slice of a generalized Hénon map contains essentially complete information, we expect that this can happen only if \(f_1\) and \(f_2\) are related by some algebraic correspondence. This question was raised in [73], Remark 4.4 for \(f_2 = f_1^{-1}\), and a complete understanding would imply the main conjecture of [73] . The analogous question of existence of local biholomorphisms between Julia sets for 1-dimensional rational maps was addressed in [74] , [97] , [106] .

Since a local unstable slice of a generalized Hénon maps contains essentially a complete information about unstable multipliers, the previous question is reminiscent of the classical “spectral rigidity” problem:

We refer to  [96] for a proof that the list of moduli of all multipliers determine a finite set of conjugacy classes of rational map of the Riemann sphere.

We denote in this section by \(f\) a complex Hénon map and by \(\mu \) its unique measure of maximal entropy [17] , [16] , [139] . We are interested in the statistical properties of \(\mu \) and of other natural invariant measures associated to such systems.

9.1. Thermodynamics for Hénon maps

Consider a continuous function \(\phi \colon \mathbb C^2 \to \mathbb R\), that will be called a weight . Following [131] one can define the pressure \(P(\phi )\) as

\[P(\phi ) := \sup \big (h_\nu + \langle \nu ,\phi \rangle \big ),\]

where the supremum is taken over all invariant probability measures \(\nu \) for \(f\) and \(h_\nu \) denotes the measure-theoretic entropy of \(\nu \). A measure \(\nu _0\) maximising the above supremum is called an equilibrium state associated to \(\phi \) and is necessarily ergodic when it is unique. The equilibrium state associated to \(\phi \equiv 0\) is the measure of maximal entropy \(\mu \). We refer to [130] for an account on the properties of equilibrium states in one-dimensional complex dynamics and to [7] , [45] , [47] and references therein for the case of real Hénon maps and diffeomorphisms of compact manifolds satisfying some hyperbolicity assumptions.

Problem 4.

Prove the existence and the uniqueness of the equilibrium state \(\mu _\phi \) associated to any sufficiently regular weight \(\phi \) (for instance, every Hölder continuous \(\phi \), and possibly with some bound on \(\max \phi - \min \phi \)).

Recall that saddle points are equidistributed with respect to the measure of maximal entropy [15] . Namely, we have

\(\seteqnumber{0}{}{5}\)

\begin{equation} \label {eq:convergence-saddle} \frac {1}{d^n} \sum _{x \in SP_n} \delta _{x}\to \mu , \end{equation}

where \(d\) is the algebraic degree of \(f\) (or, equivalently, \(\log d\) is the topological entropy of \(f\), and the measure-theoretic entropy of \(\mu \)) and \(SP_n\) is the set of the saddle \(n\)-periodic points of \(f\).

Question 35.

Suppose \(\phi \) is sufficiently regular, so that the equilibrium state \(\mu _\phi \) exists and is unique. Is it true that

\(\seteqnumber{0}{}{6}\)

\begin{equation} \label {eq:convergence-saddle-weights} \frac {1}{e^{n P(\phi )}} \sum _{x \in SP_n} e^{S_n (\phi )} \delta _x \to \mu _\phi \quad ? \end{equation}

A version of the previous question has been established in [29] in the (expanding) setting of endomorphisms of \(\mathbb P^k_{\mathbb C}\), and in particular for polynomials maps on \(\mathbb C\).

Of a somehow different flavour, we recall that an explicit speed of convergence in ( 6 ) is unknown. We believe it is a very natural and challenging question to quantify such convergence when testing against sufficiently regular functions.

Question 36.

Is the convergence ( 6 ) exponentially fast against Hölder continuous observables? Is that also the case for ( 7 )?

9.2. Statistical properties of equilibrium states and spectral gap for the transfer operators

Suppose the existence and the uniqueness of an equilibrium state \(\mu _\phi \) have been established. The (deterministic) problem of describing all orbits in the support of \(\mu _\phi \) is essentially impossible as this support should be contained in the set of points with chaotic behaviour in both forward and backward time. It is natural to adopt a probabilistic (or statistical) approach to this problem, to consider an observable \(g\colon \mathbb C^2 \to \mathbb R\), and to view the sequence \(\{g\circ f^j\}_{j \in \mathbb N}\) as a sequence of random variables on the probability space \((\mathbb C^2, \mu _\phi )\). Since \(\mu _\phi \) is invariant, these random variables have the same distribution. They are however not independent, since they arise from a deterministic setting. The first goal is thus to show that the correlations \(\langle \mu _\phi , g\circ f^{j_1} \cdot g\circ f^{j_2} \rangle - \langle \mu _\phi , g \rangle ^2 \) go to zero in a quantifiable way, as \(|j_2-j_1|\to \infty \), see for instance [148], Problem 2 . When this happens and the convergence is fast enough, the sequence \(\{g\circ f^j\}_{j \in \mathbb N}\) is then expected to satisfy a list of properties which are typical of independent identically distributed (i.i.d.) random variables.

As a first step, since \(\mu _\phi \) is ergodic, Birkhoff theorem asserts that

\(\seteqnumber{0}{}{7}\)

\begin{equation} \label {eq:birkhoff} \frac {1}{n} S_n (g) (x):= \frac {1}{n} (g (x) + g\circ f (x) + \dots + g\circ f^{n-1} (x)) \to \langle \mu _\phi , g \rangle := \int _{\mathbb C^2} g\, {\rm d}\mu _\phi \end{equation}

for \(\mu _\phi \)-almost every \(x\) and every \(g\in L^1 (\mu _\phi )\). This can be seen as a version of the law of large numbers in this setting. The next step is to show the Central Limit Theorem (CLT) for sufficiently regular observables. As in the case of i.i.d. random variables, this CLT gives the rate of the above convergence ( 8 ).

Problem 5.

Show that \(\mu _\phi \) satisfies the CLT for Hölder continuous observables. Namely, prove that, for any Hölder continuous observable \(g\), there exists \(\sigma \geq 0\) such that for any interval \(I \subset \mathbb R\), we have

\[ \lim _{n\to \infty } \mu _\phi \left (\left \{ \frac {S_n (g) - n\langle \mu _\phi ,g\rangle }{\sqrt {n} } \in I \right \}\right ) = \begin {cases} 1 \mbox { when } I \mbox { is of the form } I=(-\delta ,\delta ) & \mbox { if } \sigma ^2=0,\\ \frac {1}{\sqrt {2\pi \sigma ^2}}\displaystyle \int _I e^{-t^2 / (2\sigma ^2)}\, {\rm d}t & \mbox { if } \sigma ^2 >0. \end {cases} \]

In the case of the maximal entropy measure \(\mu \), the CLT was established in [31] . A natural question is also to characterize the observables for which \(\sigma =0\).

Sequences of (almost) independent random variables are also expected to satisfy large deviations properties. Recall that a coboundary \(g\) is an observable of the form \(\varphi \circ f - \varphi \).

Problem 6.

Show that \(\mu _\phi \) satisfies the Large Deviation Principle (LDP) for Hölder continuous observables. Namely, prove that, for any Hölder continuous observable \(g\) with \(\langle \mu _\phi , g\rangle =0\) and which is not a coboundary, there exists a non-negative, strictly convex function \(c\) which is defined on a neighborhood of \(0 \in \mathbb R\), vanishes only at \(0\), and such that, for all \(\epsilon > 0\) sufficiently small,

\[ \lim _{n\to \infty } \frac {1}{n} \log \mu _\phi \left (\left \{ x \in X\colon \frac {S_n(g)(x) }{n} >\epsilon \right \}\right ) = -c(\epsilon ).\]

Note that this question is still open even for the measure of maximal entropy.

A possible unified approach to the above statistical properties would be to find Banach spaces (containing all Hölder continuous functions) where a suitable Ruelle-Perron-Frobenius (transfer) operator associated to \(f\) would turn out to be a strict contraction on the complement of an invariant line, see for instance [7] , [83, 131] . In the case of endomorphisms of \(\mathbb P^k_{\mathbb C}\) in any dimension (in particular for any \(1\)-dimensional complex polynomial), this is the main result of [28] (see also [112] , [133] ).

Question 37.

Do there exist norms for functions on the Julia set which are bounded on Hölder continuous functions, contract (on the complement of an invariant line) under the action of \(f_*\) (or, more generally, of \(f_* (e^{\phi -P(\phi )} \cdot )\)), and such that the contraction is stable by perturbation of \(\phi \)?

In the case of hyperbolic maps, such a good Banach space has been introduced by Blank-Keller-Liverani [35] , [105] . The norm is obtained by combining a regularity condition on the unstable manifolds together with a dual condition on the stable manifolds. Note that this was the starting point of a long story (see, e.g., [84] , [8] ). As Hénon maps are only non-uniformly hyperbolic (so that stable and unstable manifolds do not behave nicely in general) the above result does not apply here.

A positive answer to Question  52 would also give a unified proof for many statistical properties of independent interest (including the Large Deviations as in Problem  51 ), without the need of an ad hoc proof for each of them. For instance, the Local Central Limit Theorem (LCLT) and the Almost Sure Invariance Principle (ASIP) are both satisfied by sequences of i.i.d., and provide stronger results than the CLT, see, e.g., [128] , [83] for definitions and criteria.

Problem 7.

Let \(\mu _\phi \) as in Problem  47 . Show that all Hölder continuous observables which are not coboundaries satisfy the LCLT and the ASIP with respect to \(\mu _\phi \).

Recall that the ASIP implies the Almost Sure Central Limit Theorem and the Law of the Iterated Logarithm.

9.3. Higher dimension and other generalizations

Until now, we restricted our attention to Hénon maps, i.e., polynomial automorphisms of \(\mathbb C^2\). On the other hand, Problems  51 and 53 , and Question  52 make perfect sense for the equilibrium measures of general rational maps once this measure has been successfully defined. We review below some partial results that have been obtained in more general (invertible) settings than Hénon maps.

A polynomial automorphism of \(\mathbb C^k\) is said to be regular if the indeterminacy sets of the extensions to \(\mathbb P^k_{\mathbb C}\) of \(f\) and \(f^{-1}\) are non-empty and disjoint (observe that every Hénon map in dimension 2 satisfies this assumption, as these two sets are two distinct points). The construction of the measure of maximal entropy is given in [139] , and the equidistribution of saddle points with respect to this measure is proved in [64] (see [31] , [58] for the exponential mixing and the CLT in this case). More generally, one can also consider birational meromorphic maps of \(\mathbb P^k_{\mathbb C}\), see [10] , [56] , [54] , [69] for the construction of the measure of maximal entropy and its properties.

Given integers \(1\leq p<k\) and open bounded convex domains \(M \Subset \mathbb C^p\) and \(N\Subset \mathbb C^{k-p}\), a horizontal-like map is a proper holomorphic map from a vertical subset to a horizontal subset of \(M\times N\) which geometrically expands in \(p\) directions and contracts in \(k-p\) directions, see [62] for the precise definition. In this setting, the unique measure of maximal entropy has been constructed and studied in [59] , [62] , [68] . In the invertible case, the CLT for this measure can be deduced from [31] .

One can also consider automorphisms of compact Kähler manifolds, see for instance [42] , [61] , [69] for the construction of the measure of maximal entropy and its properties. This setting shares a number of features with that of Hénon maps (in dimension 2) and regular automorphisms (in any dimensions). On the other hand, the compactness of the manifold makes it more difficult to apply pluripotential techniques as in the case of Hénon maps. For instance, the proof of the CLT for the measure of maximal entropy, given in [30] , requires the use of the theory of superpotentials on such manifolds [63] .

\[f(x, y)=(y, F(y)-\delta x)\]

with cycles of length \(\deg (F)+2\). Write \(F(y)=a_0+\cdots + a_dy^d\), and let \(y_0, ..., y_{d+1}\) be variables ranging over \(k\). Then, insisting that \(f\) sends

\[a_0+a_1y_n+\cdots + a_dy_n^d-\delta y_{n-1}=y_{n+1},\]

for all \(n\;(\mathrm {mod}\ d+2)\). One checks that the determinant of the associated Vandermonde-like matrix

\[\begin {pmatrix} 1 & y_0 & \cdots & y_0^d & -y_{d+1} \\ 1 & y_1 & \cdots & y_1^d & -y_{0} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & y_{d+1} & \cdots & y_{d+1}^d & -y_{d} \end {pmatrix} \]

is not identically zero (e.g., substituting \(y_{d+1}=y_d\) into this determinant gives \(\pm (y_d-y_{d-1})\prod _{0\leq i<j\leq d}(y_j-y_i)\), which is itself not identically zero), and so this matrix is invertible over some affine-open subset of \(k^{d+1}\). Here, one can find coefficients \(a_0, ..., a_d\), and \(\delta \) of \(f\) which enact ( 9 ).

Recently, Hyde and Doyle  [67] exhibited single-variable polynomials over number fields with more preperiodic points than this sort of naive interpolation construction gives. One might ask if similar phenomena could be exploited for generalized Hénon maps.

Next, it is natural to ask about bounds in the other direction. In analogy to the Uniform Boundedness Conjecture of Morton and Silverman  [120] , it is natural to posit the following, in which \(\operatorname {Per}(f)\) is the set of periodic points of \(f\) over the algebraic closure of \(K\).

It seems reasonable to posit something even stronger than Conjecture  65 . Write \(\log ^+ x=\log \max \{1, x\}\) for \(x\in \mathbb {R}^+\), and for an absolute value \(|\cdot |_v\), set

\[\|x_1, ..., x_m\|_v=\max \{|x_1|_v, ..., |x_m|_v\}.\]

Recall that a number field \(K\) comes equipped with a standard set \(M_K\) of absolute values, and we define the naive Weil height of \(P\in \mathbb {A}^N(K)\) to be

\[h(P)=\sum _{v\in M_K}\frac {[K_v:\mathbb {Q}_v]}{[K:\mathbb {Q}]}\log ^+\|P\|_v.\]

Kawaguchi  [99] constructed a canonical height \(\hat {h}_f\) associated to a generalized Hénon map, which differs by a controllable amount from the naive height, and interacts favorably with the dynamics of \(f\), satisfying for example

\[\hat {h}_f\circ f + \hat {h}_f\circ f^{-1}=\left (d+\frac {1}{d}\right )\hat {h}_f,\]

and \(\hat {h}_f(P)=0\) if and only if \(P\) is periodic. In light of partial results in this direction  [93] , it seems reasonable to conjecture the following strengthening of Conjecture  65 .

Finally, let \(f\) be a generalized Hénon map defined over a number field \(K\) with good reduction away from some finite set \(S\) of primes (so, the coefficients are \(S\)-integers, and \(a_d\) and \(\delta \) are \(S\)-units), and let \(P_0\in (\mathcal {O}_{K, S})^2\) be some non-periodic point. Set \(P_{n+1}=f(P_n)\), for \(n\geq 0\), and

\[\mathfrak {a}_n = \gcd (x(P_n)-x(P_0), y(P_n)-y(P_0))\subseteq \mathcal {O}_{K, S}.\]

That is, \(\mathfrak {a}_n\) is the largest ideal such that \(f^n(P)\equiv P\) modulo \(\mathfrak {a}_n\). Then \(\mathfrak {a}_n\) is a divisibility sequence, i.e., \(m\mid n\Rightarrow \mathfrak {a}_m\mid \mathfrak {a}_n\), which we will call a Hénon divisibility sequence . In the case \(\mathcal {O}_{K, S}=\mathbb {Z}\), we may identify the ideals with their unique positive generators, and think of this as a sequence of positive integers.

In analogy to other divisibility sequences, we probably expect this sequence to grow slowly. By comparing to the height of \(P_n\), one easily obtains an upper bound of size \(C^{d^n}\), for some \(C\), on the norm of each of the terms in the gcd, but the gcd itself should usually be much smaller.