Received: 2 March 2016 / Revised: 15 October 2016 / Accepted: 23 October 2016
Abstract
Keywords
Vector flows, Boundary effects, Convexity, Complexity, Holography
1. Introduction

This paper is about the gradient flows on compact $ 2$-dimensional surfaces, thus the reference to [Abbott1992] In [Abbott1992], the drama unfolds in the Euclidean plane, the Flatland , while here we will tell a story that takes place in the 2D-land , a compact Riemannian surface. × 1 in the title. In other words, we are interested in solutions of ordinary differential equations (ODE's) on compact surfaces $ X$ with boundary. The ODE's are represented by smooth vector fields $ v$ on $ X$. We assume that $ v$ admits a global potential $ f\colon X \to \R$ such that $ df(v) > 0$ away from the points $ x$ where $ v(x) = 0$.
The article is an informal introduction into the philosophy and some key results from [Katz2009],[Katz2014a],[Katz2014b],[Katz2014c],[Katz2015],[Katz2016a],[Katz2016b],[Katz2016c], as they manifest themselves in the dimension two. Our strongest results deal with so called traversing vector fields on smooth compact manifolds $ X$ with boundary. (By Lemma 5.1, these are exactly the vector fields that are gradients of smooth functions $ f\colon X \to \R$ with no critical points.)
Definition 1.1.
We say that a non-vanishing vector field $ v$ on a compact surface/smooth manifold $ X$ is traversing if all its trajectories are closed segments or singletons; the ends of these segments, as well as the singletons, reside in the boundary $ \d X$.Thus, for a traversing vector field $ v$, no trajectory belongs to the interior of $ X$: it reaches the boundary $ \d X$ in both "finite positive and negative times".
The main goal of our efforts is to understand the connection between the geometry of the integral curves of the $ v$-flow, as they interact with the boundary $ \d X$ of a given manifold $ X$, and the topology of $ X$. We are especially interested in describing the restrictions, imposed on $ X$ by assuming that it admits a traversing vector field $ v$ whose trajectories $ \g$ intersect $ \d X$ in such a way that the resulting combinatorial tangency patterns (see Definition 7.1 and Lemma 7.1) are prescribed a priory .
Along the way, we produce various invariants that distinguish between such traversing flows on $ X$ The flows and the vector fields here are considered up to the natural action of the diffeomorphism group $ \mathsf{Diff}(X)$ on them. × 2. The invariants reflect complexities of flow-induced natural stratifications (see Fig. 5) of $ X$. Then we employ these flow invariants to manufacture a variety of new smooth topological invariants of $ X$ itself. In [Katz2009], [Katz2014a],[Katz2014b],[Katz2014c],[Katz2015],[Katz2016a],[Katz2016b],[Katz2016c] and [Alpert and Katz2015], we use a variety of standard algebraic and geometric topology tools to compute or to estimate from below the new invariants. However, for this exposition, the reader is expected to be familiar only with the homology of compact surfaces and with their fundamental groups. We also assume some familiarity with the basic notions of the Morse Theory.
Although the class of manifolds with boundary is wider than the class of closed manifolds, the vector fields of the kind that we investigate do not exist on closed manifolds (a crude analogy of this phenomenon is provided by the Dirichlet boundary problems, which make little sense on closed Riemannian surfaces). Therefore it worth stressing that most of our results are not generalizations of some facts, valid for closed manifolds. In fact, often we drill holes in a given closed manifold $ Y$ to manufacture a manifold $ X$ with boundary and use some flow-generated invariants of $ X$ to produce new invariants of the closed $ Y$.
Let us now concentrate on the flows on $ 2$-dimensional surfaces, the main subject of this paper. The remarkable convergence of topological, geometrical, and analytical approaches to the study of closed surfaces is widely recognized by the practitioners for more than a century. We will exhibit a similar convergence of different investigative approaches to gradient flows on surfaces with boundary . Because the "rigid" topology of surfaces is understood so well, no new invariants of surfaces will emerge; however, we will get new expressions of classical invariants in terms of the $ 2$-dimensional flows (see Lemma 3.1, Theorem 3.1, Corollaries 4.1, 4.2).
In particular, we take advantage of the relative simplicity of $ 2$-dimensional flows to illustrate and popularize the main ideas of our recent research of, so called, traversally generic flows (see Definition 5.1 and Definition 3.2 from [Katz2014b] for the multidimensional case) on manifolds with boundary.
When the results are specific to dimension two, their validation will be presented in detail. The multidimensional arguments that resist significant simplifications in dimension two will be described and explained in general terms. Generically (that is, for a dense and open set in the space of all traversing vector fields on a given surface), where the flow line is tangent to the boundary of a surface, the boundary can be either convex or concave with respect to the flow (see Fig. 1). In particular, in dimension two, for a generic $ v$, no $ v$-trajectory is cubically tangent to the boundary.

In what follows, we are motivated by few natural questions.
Question 1.1.
Given a compact connected surface $ X$ with boundary, what is the minimal number of concave/convex tangency points that a gradient or a traversing vector flow on $ X$ may have? How these minima can be expressed in terms of the topological invariants of $ X$?Lemma 3.1, Corollaries 4.1, 4.2 provide answers to Question 1.1. Theorem 1.1 below describes the flavor of these results. It is implied by Corollary 4.2 and Lemma 5.1.
Theorem 1.1.
Let a surface $ X$ be formed by removing $ k$ open disks from a closed orientable surface $ Y$, the sphere with $ g$ handles.Then, for an open and dense set in the space of all traversing vector fields $ v$ on $ X$, the number of concave $ v$-flow tangencies to $ \d X$ is greater than or equal to $ 4g - 4 + 2k$.
Moreover, this inequality turns into an equality if and only if the trajectories of $ v$ are tangent to $ \d X$ in a concave manner only (as in Fig. 1, the right diagram).
We denote by $ gc^+(X)$ the minimal number of concave tangencies to $ \d X$ that a generic traversing vector flow on $ X$ may have, and view $ gc^+(X)$ as a measure of complexity of $ X$. In fact, a similar invariant makes sense for $ n$-dimensional manifolds $ X$: it is based on counting the flow trajectories that are simply tangent (see Definition 7.1) to $ \d X$ exactly $ n-1$ times, and then taking the minimum of these counts over all such flows on $ X$ ([Alpert and Katz2015]; [Katz2016b]).
The next question is a close relative of Question 1.1.
Question 1.2.
Which compact connected surfaces with boundary admit traversing vector flows that have only concave/convex tangencies?The next theorem provides a complete answer.
Theorem 1.2.
- Any connected compact surface $ X$ with boundary, but the disk and the M[U+00A8]obius band, admits a traversing vector field $ v$ with only concave tangency points to $ \d X$.
- The disk and the M[U+00A8]obius band do not admit such a vector field.
- Any connected compact surface with boundary, that admits a traversing vector field with convex tangency points only is a disk or an annulus In the case of annulus, this set is empty. × 3. So, the annulus is the only connected compact surface that admits both concave and convex traversing vector fields.
Theorems 6.1 and 6.2 generalize Theorem 1.1. They deliver more nuanced answers to Questions 1.1 and 1.2.
Now we are in position to formulate a "more existential" meta-question:
Question 1.3.
Given a traversing vector field $ v$ on a connected compact surface/ manifold $ X$, are there some $ v$-flow generated structures on the boundary $ \d X$ that will allow for (perhaps, partial) reconstruction of $ X$ and the flow?We call such desirable structures holographic since the information, recorded on $ 1$-dimensional [in general, $ (n-1)$-dimensional] screen, makes it possible to restore the topology of $ X$ and the $ 2$-dimensional [in general, $ n$-dimensional] flow on it.
Let us describe one holographic structure that dominates the landscape. Take a compact connected surface $ X$ with boundary and a traversing vector field $ v$ on it. For each point $ x \in \d X$, where $ v$ points inward of $ X$ or is tangent to $ \d X$, consider the the $ v$-trajectory $ \g$ through $ x$. Let $ C_v(x) \in \d X$ be the first along $ \g$ point, where $ \g$ exits $ X$ or touches its boundary. We think of the point-event $ x$ as the cause for the point-event $ C_v(x)$. This interpretation will be justified in Sect. 8, Example 8.1.
The correspondence $ x \leadsto C_v(x)$ gives rise to a well-defined map \begin{eqnarray*} C_v: \d^+X(v) \longrightarrow \d^-X(v) \end{eqnarray*} from a portion $ \d^+X(v)$ of $ \d X$, where $ v$ points inward of $ X$ or is tangent to $ \d X$, to the closure $ \d^-X(v)$ of the complementary portion $ \d X \setminus \d^+X(v)$. For a generic That is, for an open and dense set in the space of all traversing vector fields on $ X$. × 4 $ v$, both portions share a common boundary: $ \d(\d^+X(v)) = \d(\d^-X(v))$.
We may view $ C_v$ as defining a partial order among points of $ \d X$ (see Sect. 8 for details).
The map $ C_v$ is discontinuous; in fact, we assign the most important role to the discontinuities of $ C_v$. (See Fig. 7 for a pictorial example of $ C_v$.)
To get a feel for the "physics inspired" spirit of Question 1.3, imagine that we do not have access to the interior of a mystery surface $ X$, but have positioned a set of detectors along its boundary, detectors that register where each particle of a traversing $ v$-flow enters $ X$ and where its first exit point on the boundary $ \d X$ is located. The causality map $ C_v$ records all such data. So we asking whether the data are sufficient for a reconstruction of the pair $ (X, v)$.
Theorem 8.1 is a generalization of the following theorem.
Theorem 1.3.
(The Causal Holography Theorem) For an open and dense set in the space of all traversing vector fields $ v$ on a compact connected surface $ X$ with boundary, the causality map $ C_v\colon \d^+X(v) \to \d^-X(v)$ determines the topology of $ X$ and the $ v$-oriented un-parametrized $ v$-flow curves on it, up to a diffeomorphism of $ X$ which is the identity on $ \d X$.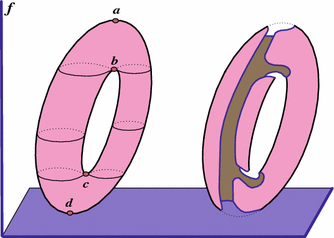
So Theorem 1.3 gives a positive answer to Question 1.3. Of course, if a surface $ X$ and a vector field $ v$ on it are real analytic and the boundary of $ \d X$ is analytic as well, then one should expect some rigid dependence of the flow in $ X$ on the boundary data. Somewhat surprisingly, Theorem 1.3 tells us that, in the smooth category, a similar topological rigidity is valid!
2. On Morse Theory on Surfaces with
Boundary and Beyond

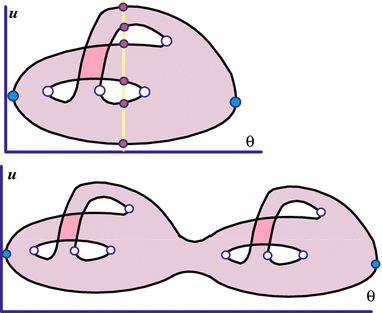
In this section, we present our approach to the Morse Theory of gradient flows, in which the boundary effects (like the convexity and the concavity) rule. Morse Theory , the classical book of [Milnor1965], starts with the canonical picture of a Morse function $ f\colon T^2 \to \R$ on a 2-dimensional torus $ T^2$ (see Fig. 2). It is portrayed as the height function $ f$ on the torus $ T^2$ residing in the space $ \R^3$. The height $ f$ has four critical points : $ a, b, c$, and $ d$ so that \begin{eqnarray*} f(a) > f(b) > f(c) > f(d). \end{eqnarray*} Recall that a point $ z$ is called critical if the differential $ df$ of $ f$ vanishes at $ z$. In the vicinity of each critical point $ z$, $ T^2$ admits a pair of local coordinate functions, say $ x$ and $ y$, so that locally the function $ f$ acquires the form \begin{eqnarray*} f(x, y) = f(0, 0) \pm x^2 \pm y^2, \end{eqnarray*} where the signs may form four possible combinations.
We call a vector field $ v$, tangent to $ T^2$, $ f$- gradient-like if $ df(v) > 0$ everywhere outside of the set $ Cr(f)$ of critical points.
If the torus is "slightly slanted" with respect to the vertical coordinate $ f$ in $ \R^3$, then the following picture emerges. The majority of downward trajectories of the $ f$-gradient-like flow $ \{\Phi_t\}_{t \in \R}$ that emanate from $ a$, asymptotically reach $ d$. There are two trajectories that asymptotically link $ a$ with $ b$, and two trajectories that link $ a$ with $ c$. No (unbroken) trajectory asymptotically connects $ b$ to $ c$.
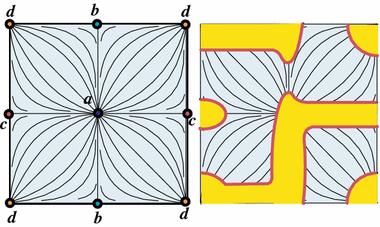
Perhaps, a more transparent depiction of the gradient-like flow $ \{\Phi_t\}_{t \in \R}$ is given in Fig. 3, where the torus is shown in terms of its fundamental domain, the square. To form $ T^2$, the opposite sides of the square are identified in pairs.
The Morse Theory is concerned with the sets of constant level $ \{f^{-1}(\a)\}_{\a \in \R}$ and with the below constant level sets $ \{f^{-1}((-\infty, \a))\}_{\a \in \R}$. The main observation is that the topology of these sets is changing in an essential way only when the rising level $ \a$ crosses the critical values \begin{eqnarray*} Cr(f) = \{f(a), f(b), f(c), f(d)\}. \end{eqnarray*} In the rest of this section, we assume that all the critical values are distinct.
Each such "critical crossing" results in an elementary surgery on the set $ \{f^{-1}((-\infty, \a))\}_{\a \in \R}$, where $ \a$ is just below a critical value $ \a_\star \in Cr(f)$. For a small $ \e > 0$, an elementary surgery \begin{eqnarray*} f^{-1}((-\infty, \a_\star -\e)) \Rightarrow f^{-1}((-\infty, \a_\star + \e)) \end{eqnarray*} attaches the handle $ f^{-1}((\a_\star -\e, \a_\star + \e))$ to the set $ f^{-1}((-\infty, \a - \e))$. Eventually, when $ \a$ rises above $ f(a)$, the entire topology of torus $ T^2$ is captured by a sequence of these elementary surgeries.
From a different angle, the knowledge of how the critical points $ a, b, c, d$ interact via the trajectories of the $ \Phi_t$-flow is also sufficient for reconstructing the surface $ T^2$, as the left diagram in Fig. 3 suggests [see [Cohen1991] for multidimensional generalizations].
Note that, in the vicinity of each critical point, the gradient flow exhibits discontinuity : small changes in the initial position of a point $ z$, residing in the vicinity of a critical point, result in significant differences in the position of $ \Phi_t(z)$ for big positive/small negative values of $ t$ (see Fig. 4). In fact, this discontinuity of the gradient flow, expressed in terms of the stable and unstable manifolds of critical points [see [Milnor1965]], captures the topology of the surface!
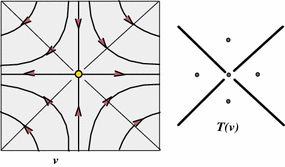
As a result of gradient flow discontinuity, the space of trajectories $ \mathcal T(v)$ is pathological (non-separable). The space $ \mathcal T(v)$ is constructed by declaring equivalent any two points that reside on the same trajectory.
Originally, the Morse theory of smooth functions and their gradient flows on compact manifolds $ X$ with boundary has been studied (under general boundary conditions) in the papers of [Morse1929] and of [Morse and Van Schaack1934]. See [Barannikov1994] for the case $ X$ being a ball.
The Morse Theory on manifolds with boundary can be viewed as a very special instance of the Morse Theory on stratified spaces (the two strata $ \d X$ and $ X$ form the stratification). The latter was developed by Goresky and MacPherson in [Goresky and MacPherson1983a],[Goresky and MacPherson1983b],[Goresky and MacPherson1989]. See also [Hardon2004], [Laudenbach2011] for constructions of the Morse-Smale differential complex on manifolds with conners.
If the Morse function $ f\colon X \to \R$ is assumed to be constant on $ \d X$, then its gradient flow interacts with the boundary in a constrained way. Then the relative topology of the pair $ (X, \d X)$ can be captured in the ways analogous to the previous description of the Morse Theory on torus.
In this paper, we offer a different philosophy for the Morse Theory on compact surfaces/manifolds $ X$ with boundary. To formulate it, let us revisit our favorite closed surface, the torus. By deleting from $ T^2$ small disks, centered on the points of the critical set $ Cr(f)$, we manufacture a surface $ X$ whose boundary is a disjoint union of four circles. Evidently, $ f\colon X \to \R$ has no critical points at all. Still it has a nontrivial topology! Can this topology be reconstructed from some data, provided by the critical-point-free $ f$ and its non-vanishing gradient-like vector field $ v$? An experienced reader would notice that the restriction $ f|_{\d X}$ has critical points (maxima and minima), some of which interact along the boundary (with the help of a gradient-like vector field $ v^\d$, tangent to $ \d X$). However, it is quite clear that these interactions are not sufficient for a reconstruction of the topology of $ X$! In fact, a reconstruction of the surface $ X$ becomes possible if one introduces additional interactions between the points of $ Cr(f|_{\d X})$ that occur "through the bulk $ X$" and are defined with the help of both vector fields $ v$ and $ v^\d$. This observation has been explored by a number of authors ([Hardon2004],[Laudenbach2011]), but it is not the world view that we are promoting here.
To dramatize further the situation we are facing, let us place four small disks, centered on the critical points of $ f\colon T^2 \to \R$, into a single open disk $ D^2$ and form $ X = T^2{\setminus}D^2$ (see Fig. 3, the right diagram). Again, $ f|_X\colon X \to \R$ has no critical points, the gradient-like vector field is non-vanishing on $ X$, but its topology of $ X$ is nontrivial. This time, the boundary $ \d X$ of the punctured torus $ X$ is just a single circle! Let us keep this challenge in mind.
So can one propose a "Morse Theory" that is not centered on critical points? The answer is affirmative. It relies on the following observation. Typically, in the vicinity of $ \d X$, the $ v$-trajectories are interacting with the boundary in a number of very particular and stable ways: they are either transversal to $ \d X$, or are tangent to it in a concave or convex fashion It is possible to have a vector field $ v$ for which some trajectories will be cubically tangent to the boundary, but the majority of $ 2$-dimensional vector fields $ v$ avoid such cubic tangencies [Katz2014b]. × 5 (see Fig. 1). So the boundary $ X$ may be "wiggly" with respect to the flow. We claim that this geometry of the $ v$-flow in relation to the boundary $ \d X$ is the crucial ingredient for reconstructions of $ X$ in terms of the flow (see Sect. 8, especially Theorem 8.1).
In the vicinity of a concave tangency point, the $ v$-flow is discontinuous in the same sense as the gradient flow is discontinuous in the vicinity of its critical point: in time, close initial points become distant. In this context, the divergence of initially close points occurs due to very different travel times available to them; unlike the infinite travel time for the gradient flows of the Morse theory on closed surfaces, in the case of the non-singular gradient flows on surfaces with boundary, every point exits the surface in finite time. In particular, the surface is not flow-invariant! And again, these discontinuities of the flow reflect the topology of the surface. Let us clarify this point.
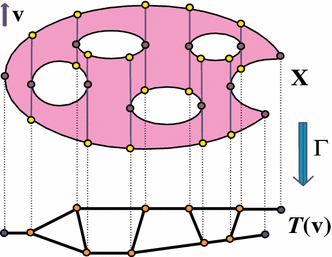
Figure 5 shows a gradient flow $ v$ on a surface $ X \subset \R^2$, the disk with $ 4$ holes. The nonsingular function $ f\colon X \to \R$ is the vertical coordinate in $ \R^2$. Each $ v$-trajectory is either a closed segment, or a singleton; so the flow is traversing. By collapsing each trajectory to a point, we create a quotient space $ \mathcal T(v)$ of trajectories. Since the flow trajectories are closed segments or singletons, this time, the trajectory space $ \mathcal T(v)$ is "decent", a finite graph with verticies of valency $ 1$ or $ 3$ only. The verticies of valency $ 3$ correspond to the points on $ \d X$ where the boundary is concave with respect to the flow, and the univalent verticies to the points on $ \d X$ where the flow is convex.
The obvious map $ \Gamma\colon X \to \mathcal T(v)$ is cellular. Moreover, because the fibers of $ \Gamma$ are contractible, $ \Gamma$ is a homotopy equivalence . In particular, the fundamental groups $ \pi_1(X)$ and $ \pi_1(\mathcal T(v))$ are isomorphic with the help of $ \Gamma$. So the trajectory spaces of generic non-vanishing gradient-like vector fields $ v$ on connected surfaces $ X$ with boundary deliver $ 1$-dimensional homotopy theoretical models of $ X$. This observation is valid for generic $ n$-dimensional non-vanishing gradient-like flows [Katz2014c], but its justification requires an involved argument.
3. Vector Fields and Morse Stratifications
on Surfaces

To achieve some uniformity of notations, put $ \d_0^+X =_{\mathsf{def}} X$ and $ \d_1X =_{\mathsf{def}} \d X$.
Following [Morse1929], for any vector field $ v$ on a compact surface $ X$, such that the vector field does not vanish at the points of $ \d X$, we consider the closed locus $ \d_1^+X(v)$, where the vector field is pointing inside $ X$ or is tangent to $ \d X$, and the closed locus $ \d_1^-X(v)$, where it points outside or is tangent to $ \d X$. The intersection \begin{eqnarray*} \d_2X(v) =_{\mathsf{def}} \d_1^+X(v)\cap \d_1^+X(v) \end{eqnarray*} is the locus where $ v$ is tangent to the boundary $ \d X$. Points $ z \in \d_2X(v)$ come in two flavors: by definition, $ z \in \d^+_2X(v)$ when $ v(z)$ points inside of the locus $ \d_1^+X(v)$; otherwise $ z \in \d^-_2X(v)$.
Definition 3.1.
We say that a vector field $ v$ on a compact surface $ X$ is boundary generic if:- the vector field $ v|_{\d X}$ does not vanish,
- $ v|_{\d X}$, viewed as a section of the normal $ 1$-dimensional (quotient) bundle \begin{eqnarray*} n_1 =_{\mathsf{def}} T(X)|_{\d X} \big/ T(\d X), \end{eqnarray*} is transversal to its zero section (at the points of the locus $ \d_2X(v)$).
Thus, for a boundary generic $ v$, the loci $ \d_1^\pm X(v)$ are finite unions of closed intervals and circles, residing in $ \d X$; and the loci $ \d_2^\pm X(v)$ are finite unions of points in $ \d X$ (Fig. 5).
We denote by $ \mathcal V^\dagger(X)$ the space of all boundary generic vector fields on a compact surface $ X$. It is easy to check that $ \mathcal V^\dagger(X)$ is an open and dense (in the $ C^\infty$-topology) subset of the space $ \mathcal V(X)$ of all vector fields on $ X$ ([Katz2014a]).
Let $ \chi(Z)$ denote the Euler number of a space $ Z$. Recall that $ \chi(Z)$ is the alternating sum of dimensions of the homology spaces $ \{H_i(Z; \R)\}_i$.
Since for a connected surface $ X$ with boundary $ H_2(X; \R) = 0$, we get \begin{eqnarray*} \chi(X) = 1 - \dim_\R(H_1(X; \R)). \end{eqnarray*} For a closed connected surface, \begin{eqnarray*} \chi(X) = 2 - \dim_\R(H_1(X; \R)). \end{eqnarray*}
Given a vector field $ v$ with isolated zeros, we can associate an integer $ \mathsf{ind}_x(v)$ with each zero $ x$ of $ v$. This integer is the degree of the map which, crudely speaking, takes each point $ z$ on a small circle $ C_x$ with its center at $ x$ to the unit vector $ v(z)/\|v(z)\|$. Then we define $ \mathsf{Ind}(v)$, the (global) index of $ v$, as the sum $ \sum_{\{x \in \text{ zeros of } v\}} \mathsf{ind}_x(v)$.
The Morse formula ([Morse1929]), in the center of our investigation, computes the index $ \mathsf{Ind}(v)$ of a given boundary generic vector field $ v$ on a surface $ X$ as the alternating sum of the Euler numbers of the Morse strata $ \{\d_j^+X(v)\}_{0 \leq j \leq 2}$:
| \begin{eqnarray}\label{eq1.1} \mathsf{Ind}(v) = \chi(X) - \chi(\d_1^+X(v)) + \chi(\d_2^+X(v)). \end{eqnarray} | (3.1) |
In particular, if $ v$ is a non-vanishing field in $ X$, then $ \mathsf{Ind}(v) = 0$, and we get
| \begin{eqnarray}\label{eq1.2} \frac{1}{2}\big(\#\{\d_2^+X(v)\}- \#\{\d_2^-X(v)\}\big) = \dim_\R(H_1(X; \R)) - 1, \end{eqnarray} | (3.2) |
Lemma 3.1.
Let a surface $ X$ be formed by removing $ k$ open disks from a closed surface $ Y$, the sphere with $ g$ handles. Then, for any boundary generic non-vanishing vector field $ v$ on $ X$, \begin{eqnarray*} \#\{\d_2^+X(v)\}\, \geq \, 4g - 4 + 2k. \end{eqnarray*} Moreover, $ \#\{\d_2^+X(v)\} = 4g - 4 + 2k$ only when $ \#\{\d_2^-X(v)\} = 0$.Proof.
The Euler number is additive under gluing surfaces along their boundary components. Therefore, if $ k$ disks are removed from $ Y$, the sphere with $ g$ handles, then $ \chi(X) = 2-2g - k$. Thus the formula ( (3.2) ) implies \begin{eqnarray*} \#\{\d_2^+X(v)\} \geq 4g - 4 + 2k \end{eqnarray*} for any non-vanishing $ v$. Moreover, $ \#\{\d_2^+X(v)\} = 4g - 4 + 2k$ if and only if $ \#\{\d_2^-X(v)\} = 0$, the main feature of the boundary concave vector fields (see Definition 4.1). ⬜In particular, for any non-vanishing boundary generic vector field $ v$ on a torus with a single hole, $ \#\{\d_2^+X(v)\} \geq 2$ (cf. Fig. 3).
Recall that an immersion is a smooth map of manifolds, whose differential has the trivial kernel.
Consider a smooth map $ \a\colon X \to \R^2$, which is an immersion in the vicinity of $ \d X$. Any such $ \a$ gives rise to the Gauss map $ G\colon \d X \to S^1$, defined by the formula $ G(x) = \a_\ast(\tau_x)/\| \a_\ast(\tau_x)\|$, where $ \tau_x$ is the tangent vector to $ \d X$ at $ x$. The direction of $ \tau_x$ is consistent with the orientation of $ \d X$, induced by the preferred orientation of $ X$.
Let $ \hat v$ be a non-vanishing vector field on $ \R^2$. Since the kernel of the differential of $ D\a\colon TX \to T\R^2$ is trivial along $ \d X$, the vector field $ \hat v$ defines a vector field $ \tilde v = \a^\ast(\hat v)$ on $ X$ in the vicinity of $ \d X$. The pull-back vector field $ \tilde v$ extends to a vector field $ v$ on $ X$, possibly with zeros (see [Gottlieb1996] for engaging discussions of vector field transfers and the Gauss-Bonnet Theorem).
Then the degree of the Gauss map is given by a classical Hopf formula ([Hopf1937]) \begin{eqnarray*} \deg(G) = \chi(X) - \mathsf{Ind}(v). \end{eqnarray*}
When $ \a\colon X \to \R^2$ is an immersion everywhere, the pull-back vector field $ v = \a^\ast(\hat v) \neq 0$ everywhere. Thus $ \mathsf{Ind}(v) = 0$, and, for a connected $ X$ with $ \d X \neq \emptyset$, we get \begin{eqnarray*} \deg(G) = \chi(X) = 1 - \dim(H_1(X; \R)). \end{eqnarray*} So, for immersions $ \a$, we get a new interpretation of formula ( (3.2) ):
| \begin{eqnarray}\label{eq1.3} \deg(G) = \chi(X) = \frac{1}{2} \Big(\#\{\d_2^-X(v)\} - \#\{\d_2^+X(v)\}\Big). \end{eqnarray} | (3.3) |
In particular, for a connected orientable surface $ X$ of genus $ g$ with a single boundary component,
| \begin{eqnarray}\label{eq1.4} \chi(X) = 1 - 2g = \frac{1}{2}\big(\#\{\d_2^-X(v)\} - \#\{\d_2^+X(v)\}\big). \end{eqnarray} | (3.4) |
So the number of $ v$-trajectories $ \g$ in $ X$ that are tangent to $ \d X$, but are not singletons (they correspond to points of $ \d_2^+X(v)$), as a function of genus $ g$, is greater than or equal to $ 4g - 2$!
On the other hand, when $ \d X$ is connected, by the Whitney index formula ([Whitney1937]), the degree of the Gauss map $ G\colon \d X \to S^1$ can be also calculated as $ \mu + N^+ - N^-$, where $ N^\pm$ denotes the number of positive/negative self-intersections of the curve $ \a(\d X) \subset \R^2$, and $ \mu = \pm 1$. Here is a brief description of the rule by which these self-intersections acquire polarities. Let $ p \in \a(\d X)$ be a point where the coordinate function $ y\colon \R^2 \to \R$ attends its minimum on the curve $ \a(\d X)$. If the tangent vector $ \tau_p$ at $ p$, which defines the orientation of $ \a(\d X)$, is $ \d_x$, then we put $ \mu = +1$; if $ \tau_p = - \d_x$, then $ \mu = -1$. Starting at $ p$ and moving in the direction of $ \tau_p$, we visit each self-intersection $ a$ twice and in a particular order. The first visitation defines a tangent vector $ \tau_1(a)$, the second visitation defines a tangent vector $ \tau_2(a)$. When the ordered pair $ (\tau_1(a), \tau_2(a))$ defines the clockwise orientation of the $ xy$-plane, then we attach "$ -$" to $ a$. Otherwise, the polarity of $ a$ is "$ +$".
Therefore we get a somewhat mysterious connection between the self- intersections of $ \d X$ under immersions $ \a\colon X \to \R^2$ and the tangency patterns of the flows in $ X$ that are the $ \a$-pull-backs of non-vanishing flows in the plane.
Theorem 3.1.
Let $ \hat v$ be a non-vanishing vector field in the plane $ \R^2$. Let $ X$ be a connected orientable surface of genus $ g$ and with a connected boundary. Consider an immersion $ \a\colon X \to \R^2$ such that the map $ \a\colon \d X \to \R^2$ is $ 2$-to-$ 1$ at most and the loop $ \a(\d X)$ has transversal self-intersections only. Assume that the pull-back $ v = \a^\ast(\hat v)$ is a boundary generic vector field on $ X$. Then \begin{eqnarray*} \frac{1}{2} \Big(\#\{\d_2^+X(v)\} - \#\{\d_2^-X(v)\}\Big) = N^+ - N^- \pm 1 = 2g -1, \end{eqnarray*}\begin{eqnarray*} \frac{1}{2} \Big(\#\{\d_2^+X(v)\} - \#\{\d_2^-X(v)\}\Big) + 2\, \leq N^+ + N^-, \end{eqnarray*} the latter inequality being sharp by an appropriate choice of $ \a$.
Proof.
The first formula is the result of combining the Whitney formula for $ \deg(G)$ with formulas ( (3.3) ), ( (3.4) ).By a theorem of [Guth2009], for any immersion $ \a\colon X \to \R^2$, the total number of self-intersections of the loop $ \a(\d X)$ admits an estimate \begin{eqnarray*} N^+ + N^- \geq \, 2g + 2. \end{eqnarray*} Moreover, this lower bound is realized by an immersion $ \a\colon X \to \R^2$! Therefore, by formula ( (3.4) ), the Guth inequality is transformed into \begin{eqnarray*} N^+ + N^- \geq 2+ \frac{1}{2}\big(\#\{\d_2^+X(v)\} - \#\{\d_2^-X(v)\}\big). \end{eqnarray*} Moreover, for some optimal immersion $ \a$, \begin{eqnarray*} N^+ + N^- = 2+ \frac{1}{2}\big(\#\{\d_2^+X(v)\} - \#\{\d_2^-X(v)\}\big) = 2 - \frac{1}{2\pi}\int_{\d X} K_\nu\, d\mathsf g. \end{eqnarray*} ⬜
When a surface $ X$ is oriented and a vector field $ v$ is boundary generic, then the points from $ \d_2^+X(v)$ come in two new flavors : "$ \oplus, \ominus$". By definition, a point $ a \in \d_2^+X(v)$ has the polarity "$ \oplus$" if the orientation of $ T_aX$ determined by the pair $ (\nu_a, v(a))$, where $ \nu_a$ is the inner normal to $ \d X$, agrees with the preferred orientation of $ X$. Otherwise, the polarity of $ a$ is defined to be "$ \ominus$". (These new polarities will play a crucial role in Theorem 9.2.)
Thus, for each choice of orientation of $ X$ (and hence of $ \d X$) we get a partition \begin{eqnarray*} \d_2^+X(v) = \d_2^{+, \oplus}X(v) \coprod \d_2^{+, \ominus}X(v). \end{eqnarray*} Switching the orientation of $ X$ switches the second polarities in the partition.
4.
Convexity, Concavity, and Complexity of Flows in 2D 
Definition 4.1.
We say that a boundary generic vector field $ v$ is boundary convex if $ \d_2^+X(v) = \emptyset$, and is boundary concave if $ \d_2^-X(v) = \emptyset$ (see Fig. 1).The existence of a boundary convex vector field puts severe restrictions on the topology of the surface.
Lemma 4.1.
If a compact connected surface $ X$ with boundary admits a boundary convex traversing vector field $ v$, then $ X$ is either a disk $ D^2$, or an annulus $ A^2$.Proof.
The convexity of the vector field $ v$ implies that $ X$ admits a $ (-v)$-directed continuous retraction on the locus $ \d_1^+X(v)$. Since $ X$ is connected, it follows that $ \d_1^+X(v)$ is connected as well. Thus, $ \d_1^+X(v)$ is either a circle, or a segment. In the first case, $ X$ is diffeomorphic to an annulus $ A^2$; in the second case, $ X$ is diffeomorphic to a disk $ D^2$. ⬜The same phenomenon occurs in any dimension: if a compact connected smooth $ (n+1)$-dimensional manifold $ X$ with a connected boundary admits a boundary convex gradient-like non-vanishing vector field $ v$, then $ H_n(X; \Z) = 0$ ([Katz2014a]). In other words, $ H_n(X; \Z) \neq 0$ is a topological obstruction to the existence of a boundary convex non-vanishing gradient-like vector field on $ X$.
In contrast, the boundary concave non-vanishing gradient-like vector fields are plentiful. For example, consider a radial vector field $ v$ on an annulus $ A^2$. Delete from $ A^2$ any number of pairwise disjoint convex disks and restrict $ v$ to the resulting $ 2$- disk with holes. The convexity of the removed disks implies that any disk with holes admits a boundary concave traversing vector field $ v$.
Many other surfaces admit such concave vector fields as well. Here is an important example: consider a Morse function $ f\colon Y \to \R$ on a closed surface $ Y$ and its gradient-like vector field $ v$. Then removing small convex (in the local Morse coordinates) disks, centered on the critical points, from $ Y$, produces a boundary concave non-vanishing gradient vector field on $ X$. In particular, if $ Y$ is a sphere with $ g$ handles, then one can find a Morse function with $ 2g + 2$ critical points (see Fig. 2). So the orientable surface $ X$, obtained from $ Y$ by removing $ 2g + 2$ balls, admits a non-vanishing boundary concave gradient-like vector field $ v$.
In fact, by Theorem 6.2, any connected orientable surface with boundary, but the disk, admits a boundary concave non-vanishing gradient-like vector field!
We view the integer $ c^+(v) =_{\mathsf{def}} \#(\d_2^+X(v))$ as a measure of complexity of the $ v$-flow, subject to the condition $ \mathsf{Ind}(v) = 0$ or, alternatively, subject to the condition $ v \neq 0$ .
We define the complexity of a compact connected surface $ X$ with boundary as the minimum \begin{eqnarray*} c^+(X) = \min_{\{v \neq 0\}} \{c^+(v)\}, \end{eqnarray*} where $ v$ runs over all non-vanishing boundary generic vector fields on $ X$.
By varying $ v$ within different spaces of vector fields, one may consider a variety of such minima; non-vanishing vector fields and non-vanishing gradient-like (equivalently, traversing) vector fields are the two most important cases. So we reintroduce see the paragraph that follows Theorem 1.1. × 6 the gradient complexity \begin{eqnarray*} gc^+(X) =_{\mathsf{def}} \min_{\{v \neq 0\; \text{of the gradient type}\}} \{c^+(v)\}, \end{eqnarray*} where $ v$ runs over all non-vanishing gradient-like and boundary generic (equivalently, traversing and boundary generic) vector fields on $ X$.
Evidently $ gc^+(X) \geq c^+(X)$. Let $ M$ denote the M[U+00A8]obius band. In Sect. 6, we will show that $ gc^+(M) = 1$, while $ c^+(M) = 0$. So the two notions of complexity are different!
When $ c^+(v) \leq N$, then by Lemma 3.1, $ 4g +2k -4 \leq N$, which confines $ (g, k) \in \Z_+^2$ to a triangle whose area is a quadratic function in the variable $ N$. Hence, in terms of the complexity $ c^+(v)$, we can restate the Lemma 3.1 as follows.
Corollary 4.1.
Let $ X$ be a connected compact surface with boundary. Let $ v$ be a boundary generic vector field on $ X$, subject to the condition $ \mathsf{Ind}(v) = 0$.Then the complexity of $ v$ satisfies the inequality \begin{eqnarray*} c^+(v) \geq 2\cdot \dim_\R H_1(X; \R) - 2 = -2\cdot \chi(X). \end{eqnarray*} When $ \chi(X) \leq 0$, this inequality turns into the equality $ c^+(v) = -2\cdot \chi(X)$ if and only if $ v$ is boundary concave.
As a result, for any natural $ N$, there are finitely many (counted up to a homeomorphism) connected compact surfaces of bounded complexity $ c^+(X) \leq N$. In fact, the number of such surfaces is a quadratic function in $ N$.
Example 4.1.
In fact, for any non-vanishing boundary concave vector field $ v$ on the torus with a single hole, $ \#\{\d_2^+X(v)\} = 2$. The constant vector field $ v$, being restricted to the complement to a convex disk in $ T^2$, is boundary concave and has the property $ \#\{\d_2^+X(v)\} = 2$. Thus, by Corollary 4.1, $ c^+(X) = 2$.Lemma 3.1 leads immediately to the following corollary:
Corollary 4.2.
Let $ X$ be a sphere with $ g$ handles and $ k$ holes, where $ g, k \geq 1$. If $ X$ admits a non-vanishing boundary concave vector field $ v$, then $ c^+(X) = 4g - 4 + 2k$.Given a compact surface $ X$ with boundary, we form its double $ DX =_{\mathsf{def}} X \cup_{\d X} X$ by attaching two copies of $ X$ along their boundaries. Note that $ \chi(DX) = 2\cdot \chi(X)$. Therefore, $ \chi(X) < 0$ if and only if $ \chi(DX) < 0$.
Recall that any closed orientable surface with a negative Euler number admits a metric of constant negative curvature $ -1$, the hyperbolic metric. So if $ \chi(X) < 0$, then $ DX$ admits such hyperbolic metric.
Let $ vol(DX)$ denote the hyperbolic volume of $ DX$, and let $ vol(\D^2)$ denote the volume of an ideal hyperbolic triangle $ \D^2$ in the hyperbolic plane $ \mathbf H^2$. In fact, $ vol(\D^2) = \pi$.
In $ 2D$, a remarkable convergence of topology and geometry takes place. In the spirit of this convergence, since $ \chi(DX) = -vol(DX)/ vol(\D^2)$, Corollary 4.1 admits a more geometric reformulation:
Theorem 4.1.
Let $ v$ be a non-vanishing boundary generic vector field on a compact connected and orientable surface $ X$ with boundary. Assume that $ \chi(X) < 0$ This excludes the disk and the annulus. × 7. Then the complexity of the $ v$-flow satisfies the inequality: \begin{eqnarray*} c^+(v)\; \geq \; vol(DX)/ \pi. \end{eqnarray*} Moreover, $ c^+(v) = vol(DX)/ \pi$ if and only if $ v$ is boundary concave.Theorem 4.1 admits far reaching multidimensional generalizations [see [Alpert and Katz2015], [Katz2016b]]. They are valid for, so called, traversally generic vector fields [see Definitions 5.1 and [Katz2014b]] on arbitrary smooth compact $ (n+1)$-dimensional manifolds $ X$ with boundary. Such vector fields $ v$ naturally generate stratifications of trajectory spaces $ \mathcal T(v)$, whose strata are labeled by the combinatorial patterns of tangency from the universal partially ordered set $ \Omega^\bullet_{'\langle n]}$ [see the end of Sect. 6 and [Katz2016a]]. In high dimensions, we use the simplicial semi-norms $ \|\sim\|_\D$ of Gromov [Gromov1982] on the homology $ H_\ast(X; \R)$ and $ H_\ast(DX; \R)$ (as a substitute of the hyperbolic volume) to provide lower bounds on the number of connected components of the $ \Omega^\bullet_{'\langle n]}$-strata of any given dimension. These estimates are sensitive to the algebraic nature of the fundamental groups $ \pi_1(X)$, $ \pi_1(DX)$. In particular, they are trivial for so called amenable groups [see [Gromov1982] for the definition].
5. On Spaces of Vector Fields

Recall that each trajectory $ \g$ of a traversing vector field $ v$ on a compact connected surface $ X$ must reach the boundary $ \d X$ both in positive and negative times.
We denote by $ \mathcal V_{\mathsf{trav}}(X)$ the space (in the $ C^\infty$-topology) of all traversing vector fields on a given compact surface $ X$.
We denote by $ \mathcal V_{\mathsf{grad}}(X)$ the space (in the $ C^\infty$-topology) of all gradient-like vector fields on $ X$, and by $ \mathcal V_{\neq 0}(X)$ the space of all non-vanishing vector fields on $ X$.
The next lemma says that $ v$ is traversal if and only if it is non-vanishing and gradient-like [(see [Katz2014a], Corollary 4.1, for the proof].
Lemma 5.1.
For any compact connected surface $ X$ with boundary, \begin{eqnarray*} \mathcal V_{\mathsf{trav}}(X) = \mathcal V_{\mathsf{grad}}(X) \cap \mathcal V_{\neq 0}(X), \end{eqnarray*} an open set in the space $ \mathcal V_{\mathsf{grad}}(X)$.The surfaces $ X$ and vector fields $ v$ we consider are all smooth. We can add an external collar to $ X$ to form a diffeomorphic surface $ \hat X \supset X$ and to extend $ v$ to a smooth vector field $ \hat v$ on $ \hat X$. Let $ \hat \g$ be a $ \hat v$-trajectory (or rather its germ) through a point $ x$ of $ \d X$. We can talk about order of tangency of two smooth curves, $ \hat\g$ and $ \d X$, at $ x \in \hat\g \cap\d X$ in $ \hat X$ (see Definition 7.1). We say that the tangency of $ \hat\g$ to $ \d X$ is simple if its degree is 2. When the two curves are transversal at $ x$ we say that the order of tangency is $ 1$. In fact, these notions depends only on $ (X, v)$ and not on the extension $ (\hat X, \hat v)$.
Definition 5.1.
A traversing vector field $ v$ on a compact surface $ X$ is called traversally generic , if two properties are valid:- (1) when a trajectory $ \g$ is tangent the boundary $ \d X$, then the tangency is simple,
- (2) no $ v$-trajectory $ \g$ contains more then one simple point of tangency to $ \d X$. In particular, a traversally generic $ v$ is boundary generic. × 8
We denote by $ \mathcal V^\ddagger(X)$ the space of all traversally generic vector fields on a compact surface $ X$. In fact, the notion of traversally generic vector field is available in any dimension [see [Katz2014b]].
As the name suggests, the traversally generic vector fields are typical among all traversing vector fields; furthermore, a perturbation of any traversally generic vector field is traversally generic. This is the content of the next theorem. Its validation requires an involved argument, which even in $ 2D$ resists a significant simplification [Katz2014b].
Theorem 5.1.
For any compact connected surface $ X$ with boundary, the space $ \mathcal V^\ddagger(X)$ of traversally generic vector fields is open and dense in the space $ \mathcal V_{\mathsf{trav}}(X) = \mathcal V_{\mathsf{grad}}(X) \cap \mathcal V_{\neq 0}(X)$.
6. Graph-Theoretical Approach to the
Concavity of Traversing Vector Fields in 2D

Recall that $ c^+(X) \leq gc^+(X)$. So, we start with a natural question.
Question 6.1.
Are there compact connected surfaces $ X$ with boundary for which $ c^+(X) < gc^+(X)$?On many occasions we took advantage of the fact that, for traversally generic vector fields $ v$, the trajectory spaces $ \mathcal T(v)$ are finite graph whose verticies have valency $ 1$ and $ 3$ only (see Fig. 5). Moreover, for a traversally generic boundary concave vector field $ v$, all the verticies of $ \mathcal T(v)$ have valency $ 3$. Now we will take a closer look at the graph-theoretical models of the boundary concave and traversally generic vector fields in 2D.
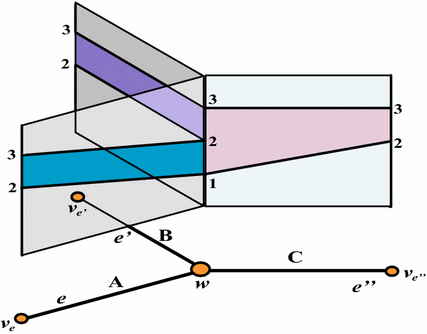
Let $ G$ be a finite connected trivalent graph with $ a$ verticies. We denote by $ \b G$ its barycentric subdivision: each edge $ e$ of $ G$ is divided by a new vertex $ v_e$, its center. We consider the finite set $ \mathsf{Tri}(G)$ of all colorings of the edges of $ \b G$ with three colors so that, at each vertex of $ G$, exactly three distinct colors are applied. Thus, $ \#\mathsf{Tri}(G) = 6^a$.
Theorem 6.1.
Let $ G$ be a finite connected trivalent graph. Each coloring $ \a \in \mathsf{Tri}(G)$ produces (in a canonical way) a compact connected surface $ X(G, \a)$ with boundary. The surface $ X(G, \a)$ admits a traversally generic concave vector field $ v(G, \a)$. The cardinality of the locus $ \d_2^+X(G, \a)\big(v(G, \a)\big)$ is the number of verticies in $ G$.Moreover, every connected surface with boundary, which admits a traversally generic concave vector field, can be produced in this way.
Proof.
Let $ \mathsf A, \mathsf B, \mathsf C$ denote the three distinct colors, and $ \mathcal P = \{\mathsf A, \mathsf B, \mathsf C\}$ the entire pallet.Consider a $ 2$-dimensional space $ Z = G \times (0, 4)$. It has singularities in the form of binders of the $ 3$-page open books (see Fig. 6). The binders correspond to the vertices of $ G$.
First, employing a given coloring $ \a$, we will construct a piecewise linear surface $ \hat X(G, \a) \subset Z$. The vector field on $ \hat X(G, \a)$ will be induced by the product structure in $ Z$.
For each edge $ e \subset G$ and its barycenter $ v_e \in \b G$, we place the interval $ v_e \times [2, 3]\subset Z$ over $ v_e$. Let $ \hat e$ be half of the interval $ e \subset G$, bounded two verticies $ v_e \in \b G$ and $ w \in G$. Over $ \hat e$, we place a strip $ E \subset Z$; its construction depends on the color attached to the interval $ [v_e, w]$ as follows:
- if the color of $ [v_e, w]$ is $ \mathsf A$, then we link the vertex $ v_e \times 2$ with the vertex $ w \times 1$ by a line in the rectangle $ R = [v_e, w] \times (0, 4)$, and the vertex $ v_e \times 3$ with the vertex $ w \times 2$ by another line in $ R$;
- if the color of $ [v_e, w]$ is $ \mathsf B$, then we link by a line in $ R$ the vertex $ v_e \times 2$ with the vertex $ w \times 2$, and the vertex $ v_e \times 3$ with the vertex $ w \times 3$ by another line;
- if the color of $ [v_e, w]$ is $ \mathsf C$, then we link by a line in $ R$ the vertex $ v_e \times 2$ with the vertex $ w \times 1$, and the vertex $ v_e \times 3$ with the vertex $ w \times 3$ by another line.
The local model of each binder implies that $ \hat X(G, \a)$ is indeed piecewise-linear surface, embedded in the singular space $ Z$. Inside $ Z$, one can smoothen the sharp edges of the boundary $ \d \hat X(G, \a)$ in order to get a smooth surface $ X(G, \a)$ (we challenge the reader to visualize this smoothing in the vicinity of point $ w \times 2$ from Fig. 6). The restriction of the product structure in $ Z$ to its subspace $ X(G, \a)$ produces a smooth non-vanishing vector field $ v(G, \a)$ on $ X(G, \a)$. Its trajectories (the vertical lines in $ Z$) will be simply tangent to $ \d X(G, \a)$ exactly at the points of the type $ w \times 2$, where $ w$ runs over the set of verticies of $ G$. By Theorem 5.1, this vector field $ v(G, \a)$ is of the gradient type.
Conversely, any traversally generic and concave vector field $ v$ on a connected compact surface $ X$ with boundary, produces a map $ \Gamma\colon X \to \mathcal T(v)$, where the space of trajectories is a finite trivalent graph. Its verticies are in 1-to-1 correspondence with the points of the locus $ \d_2^+X(v)$.
As a point $ v_e$ in the open edge $ e$ of the graph $ \mathcal T(v)$ approaches a vertex $ w$, the intersection of the $ v$-trajectory $ \g = \Gamma^{-1}(v_e)$ with the boundary $ \d X$ defines a bijection of the $ v$-ordered set $ \g \cap \d X$ of cardinality $ 2$ to a $ v$-ordered set $ \Gamma^{-1}(w) \cap \d X$ of cardinality $ 3$, the orders being respected by the bijections. This determines one of three colors we attach to the half-edge $ [v_e, w]$. Therefore the geometry of the flow determines a tricoloring of the graph $ \b {\mathcal {T}}(v)$. ⬜
Corollary 6.1.
The cardinality of the set $ \d_2^+X(v)$ is even for any boundary convex and traversally generic vector field $ v$.Proof.
For any boundary convex and traversally generic vector field $ v$, the graph $ \mathcal T(v)$ is trivalent. Its verticies are in 1-to-1 correspondence with the points of $ \d_2^+X(v)$. Since for any trivalent graph, \begin{equation*}3 \times\, \{\text{the number of verices}\} = 2 \times \, \{\text{the number of edges}\},\end{equation*} we conclude that the number of vericies in $ \mathcal T(v)$ must be even. ⬜The next theorem provides complete answers to Question 1.1 and Question 1.2.
Theorem 6.2.
- For any compact connected surface $ X$ with boundary, but the disk and the M[U+00A8]obius band, the two complexities are equal and are given by the formula: \begin{eqnarray*} gc^+(X) = c^+(X) = 2\b_1(X)-2, \end{eqnarray*} where $ \b_1(X)$ denotes the first Betti number of $ X$. Moreover, any such surface $ X$, but the disk and the M[U+00A8]obius band, admits a boundary concave traversing Even traversally generic × 9 vector field.
- In contrast, the disk $ D$ does not admit a boundary concave traversing vector field. In fact, $ c^+(D) = gc^+(D) = 0$.
- The M[U+00A8]obius band $ M$ does not admit a boundary concave traversing vector field either. However, $ M$ does admit a concave and convex non-vanishing vector field. In fact, $ c^+(M) = 0$, and $ gc^+(M) = 1$.
- The annulus is the only compact connected surface that admits both concave and convex traversing vector fields.
Proof.
Recall the topological classification of closed surfaces. Any connected orientable closed surface is either a sphere $ S$, or a torus $ T$, or a connected sum of several tori $ T$. Similarly, any connected non-orientable closed surface is a projective plane $ P$, or a connected sum of several projective planes $ P$. Evidently, any compact connected orientable surface with boundary can be obtained from a closed connected surface by deleting one or several open disks. Therefore, any compact connected orientable surface with boundary is either a disk $ D$, or an annulus $ A$, or a punctured torus $ Q = T{\setminus}D^\circ$, or a boundary connected sum of such building blocks. Similarly, any compact connected non-orientable surface with boundary is either a M[U+00A8]obius band $ M$, or a boundary connected sum of a several M[U+00A8]obius bands, or a connected sum of these surfaces with one or several annuli $ A$.By Corollary 4.1, for any compact connected $ X$ with boundary, \begin{eqnarray*} gc^+(X) \geq c^+(X) \geq 2\b_1(X) -2, \end{eqnarray*} where $ \b_1(X)$ denotes the first Betti number of $ X$. If $ X$ admits a boundary concave non-vanishing vector field $ v$, then by the same corollary, $ c^+(X) = c^+(v) = 2\b_1(X) -2$. In particular, if $ X$ admits a boundary concave traversing field, then \begin{eqnarray*} gc^+(X) = c^+(X) = 2\b_1(X) -2. \end{eqnarray*}
Note that the first Betti numbers are additive under the connected sum operation: \begin{eqnarray*} \b_1(X_1 \#_\d X_2) = \b_1(X_1) + \b_1( X_2). \end{eqnarray*}
The additivity of the first Betti numbers implies the relation
| \begin{eqnarray}\label{eq6.1} 2\b_1(X_1 \#_\d X_2) -2 = [2\b_1(X_1) -2] + [2\b_1(X_2) -2] +2. \end{eqnarray} | (6.1) |
Here is the beginning of a list of compact connected surfaces with boundary, arranged according the increasing values of their first Betti numbers:
| \begin{eqnarray} \b_1 = 0; \; & = 1; & \quad \; = 2; \qquad \qquad \cdots \nonumber \\ \; D; \; & A,\, M; \; & \; Q,\; A \#_\d A,\; A \#_\d M,\; M \#_\d M; \quad \cdots \end{eqnarray} | (6.2) |
Using the additivity of the first Betti numbers under the connected sum operation, for any compact $ X$ with boundary, we get: \begin{eqnarray*} \b_1(A \#_\d X) = 1 + \b_1(X),\;\; \b_1(M \#_\d X) = 1 + \b_1(X),\;\; \b_1(Q \#_\d X) = 2 + \b_1(X). \end{eqnarray*}
Now, let us examine the behavior of the two complexities, $ c^+(\sim)$ and $ gc^+(\sim)$, under the connected sum operation $ \#_\d$.
Given two boundary generic vector fields $ v_1$ and $ v_2$ on $ X_1$ and $ X_2$, respectively, there exists a boundary generic vector field $ w$ on $ X_1 \#_\d X_2$ such that the cardinalities of the concave and convex loci satisfy the equations Note that Eq. ( (6.3) ) resembles Eq. ( (6.1) ). × 10:
| \begin{eqnarray}\label{eq6.2} |\d_2^+(X_1 \#_\d X_2)(w)| = |\d_2^+(X_1)(v_1)| + |\d_2^+(X_2)(v_2)| + 2, \\ |\d_2^-(X_1 \#_\d X_2)(w)| = |\d_2^-(X_1)(v_1)| + |\d_2^-(X_2)(v_2)|. \nonumber \end{eqnarray} | (6.3) |
In fact, this construction of the vector field $ w$ validates the inequalities \begin{eqnarray*} c^+(X_1 \#_\d X_2) \leq c^+(X_1) + c^+(X_2) + 2, \quad {\!\!} gc^+(X_1 \#_\d X_2) \leq gc^+(X_1) + gc^+(X_2) + 2. \end{eqnarray*}
Note that when both vector fields $ v_1$ and $ v_2$ are boundary concave, then $ w$ is boundary concave as well. As a result, the set $ \mathcal C$ of compact connected surfaces Considered up to diffeomorphisms × 11 that admit non-vanishing boundary concave vector fields is closed under the boundary connected sum operation $ \#_\d$ ! Similarly, the set $ \mathcal {CT}$ of compact connected surfaces that admit boundary concave and traversing vector fields is closed under $ \#_\d$. We will see soon that $ \mathcal C$ consists of all compact connected surfaces with boundary, with a single exception --- the disk $ D$. At the same time, $ \mathcal {CT}$ consists of all compact connected surfaces with boundary, except for $ D$ and $ M$.
Let $ v_1$ and $ v_2$ be some non-vanishing boundary generic (alternatively, traversing and boundary generic) vector fields which deliver the two complexities $ c^+(X_1)$ and $ c^+(X_2)$ (alternatively, $ gc^+(X_1)$ and $ gc^+(X_2)$). The previous construction of $ w$ (extending $ v_1$ and $ v_2$ across the handle $ H$) has an implication: if $ c^+(X_1) = 2\b(X_1)-2$ and $ c^+(X_2) = 2\b(X_2) -2$, then \begin{eqnarray*} c^+(X_1 \#_\d X_2) \leq c^+(X_1) + c^+(X_2) + 2 = 2\b(X_1 \#_\d X_2) - 2. \end{eqnarray*}
Similarly, if $ gc^+(X_1) = 2\b(X_1)-2$ and $ gc^+(X_2) = 2\b(X_2) -2$, then \begin{eqnarray*} gc^+(X_1 \#_\d X_2) \leq gc^+(X_1) + gc^+(X_2) + 2 = 2\b(X_1 \#_\d X_2) - 2. \end{eqnarray*}
Since the reverse inequality holds by Corollary 4.1, we get
| \begin{eqnarray}\label{eq6.3} c^+(X_1 \#_\d X_2) = 2 \b(X_1 \#_\d X_2)-2, \end{eqnarray} | (6.4) |
Similarly, by Corollary 4.1, we get
| \begin{eqnarray}\label{eq6.4} gc^+(X_1 \#_\d X_2) = 2 \b(X_1 \#_\d X_2)-2 \end{eqnarray} | (6.5) |
Let us now compute the complexities of the surfaces $ D, A, Q$, the basic building blocks in the representation (as boundary connected sums) of orientable connected surfaces with boundary, and the complexities of the basic blocks $ M, A$, which participate in the representation of non-orientable connected surfaces with boundary.
Note that $ c^+(D) = 0 = gc^+(D)$, since $ D$ admits a convex traversing flow. By formula ( (3.2) ), $ D$ does not admit a boundary concave non-vanishing vector field.
Also $ c^+(A) = 0 = gc^+(A)$, the latter equality being delivered by the radial gradient-like vector field.
We claim that $ c^+(Q) = 2 = gc^+(Q)$. Indeed, since $ \b_1(Q) = 2$, by Corollary 4.1, we get $ c^+(Q) \geq 2$. On the other hand, there exists a trivalent graph $ G_Q$ with an appropriate tricoloring and exactly two verticies such that, applying the construction from Theorem 6.1, we produce a traversally generic vector field $ v(G_Q, \a)$ on the surface $ X(G_Q, \a) = Q$ with the cardinality $ 2$ locus $ \d_2^+X(G_Q, \a)(v(G_Q, \a))$. As a result, both complexities of $ Q$ equal to $ 2$.
The M[U+00A8]obius band $ M$ is different. We notice that $ M$ admits a non-vanishing vector field $ v$ with a single closed trajectory---the core of the M[U+00A8]obius band---and transversal to the boundary $ \d M$. Thus, $ c^+(M) = 0$.
Now consider a trivalent graph $ G_M$ ("$ \mathbf{*-\bullet\,\big< \big>}$") with a single vertex "$ \bullet$" of valency $ 3$ and a single vertex "$ *$" of valency $ 1$ (this $ G_M$ is a circle "$ \mathbf{\big<\big>}$" to which a radius "$ \mathbf{*-\bullet}$" is attached). The construction from Theorem 6.1 applies to produce a remarkable embedding of the M[U+00A8]obius band in the product $ G_M \times [0, 4]$. So we conclude that $ M$ admits a traversally generic vector field $ v_M$ (not a concave one!) with $ \d_2^+M(v_M)$ being a singleton ($ \d_2^-M(v_M)$ is a singleton as well). As a result, $ gc^+(M) \leq 1$. On the other hand, any traversally generic vector field $ v$ on $ M$ must produce the graph $ \mathcal T(v)$ which is homotopy equivalent to a circle, the homotopy type of $ M$. If $ \d_2^+M(v) = \emptyset$, this graph $ \mathcal T(v)$ has no trivalent verticies, in which case, $ \mathcal T(v)$ is homeomorphic to a circle. So $ M \to \mathcal T(v)$ must be a fibration whose fibers (the $ v$-trajectories) are segments. Moreover, thanks to the vector field $ v$, this fibration is orientable, a contradiction with the non-orientability of $ M$. Therefore, we conclude that $ gc^+(M) = 1$, while $ c^+(M) = 0$.
Let $ K =_{\mathsf{def}} M \#_\d M$, $ L =_{\mathsf{def}} A \#_\d M$, and $ N =_{\mathsf{def}} A \#_\d A$. In fact, Theorem 6.1 implies that $ Q$, $ K$, $ L$, and $ N$ are the only connected surfaces of the gradient complexity $ 2$; all of them admit boundary concave traversally generic vector fields. Indeed, just start with the tree "$ \big>\bullet-\bullet \big<$" with two trivalent verticies and consider the ways in which one can identify its four leaves in pairs. Then consider all admissible tricologings of the resulting graphs $ G$. These cases will deliver the model tricolored graphs $ G_Q, G_K, G_L, G_N$.
Therefore $ gc^+(X) = c^+(X) = 2$ only for $ X = Q, K, L, N$.
Now the rest of the surfaces (of complexities higher than $ 2$) can be obtained by applying repeatedly the connected sum operations $ X \Rightarrow X \#_\d T$, $ X \Rightarrow X \#_\d M$, and $ X \Rightarrow X \#_\d A$ to the surfaces $ X = Q, K, L, N$ of complexity/gradient complexity $ 2$.
When $ c^+(X) = 2\b_1(X) -2$ or $ gc^+(X) = 2\b_1(X) - 2$, these changes are described by formulas ( (6.4) ) and ( (6.5) ), respecively.
First, let us consider the operation $ X \Rightarrow X \#_\d M$. According to these formulas, the inequalities \begin{eqnarray*} 2\b_1(X \#_\d M) -2 \leq c^+(X \#_\d M) \leq gc^+(X \#_\d M) \leq gc^+(X) +2 \end{eqnarray*} can be reduced to \begin{eqnarray*} 2\b_1(X) \leq c^+(X \#_\d M) \leq gc^+(X \#_\d M) \leq 2\b_1(X), \end{eqnarray*} provided that $ gc^+(X) = 2\b_1(X) -2$. For such $ X$, we get again the property \begin{eqnarray*} c^+(X \#_\d M) = gc^+(X \#_\d M) = 2\b_1(X) = 2\b_1(X \#_\d M) -2. \end{eqnarray*} Similar considerations hold for the operations $ X \Rightarrow X \#_\d T$ and $ X \Rightarrow X \#_\d A$.
Therefore, by an induction in complexities, for all the surfaces $ X$, but $ D$ and $ M$, $ c^+(X) = gc^+(X) = 2\b_1(X) -2$. Moreover, all such surfaces admit boundary concave and traversing vector fields. ⬜
7. Combinatorics of Tangency for
Traversing flows in 2D

Pick an extension $ \hat X$ of a given compact surface $ X$ by adding an external collar to $ X$. Let $ \hat v$ be an extension of a given vector field $ v$ into $ \hat X$. Pick a smooth auxiliary function $ z\colon \hat X \to \R$ such that:
- 0 is a regular value of z,
- $ z^{-1}(0) = \d X$,
- $ z^{-1}((-\infty, 0]) = X$.
Definition 7.1.
Let $ \hat\g$ be a $ \hat v$-trajectory through a point $ x \in \d X$. We say that $ \hat\g$ has the order of tangency (multiplicity) $ k$ to $ \d X$ at $ x$, if $ \mathcal L_{\hat v}^{\{j\}} (z) = 0$ for all $ j < k$, and $ \mathcal L_{\hat v}^{\{k\}} (z) \neq 0$ at $ x$ This is equivalent to saying that the $ (k-1)$-st jet at $ x$ of $ z|_\g$ vanishes, but the $ k$-th jet does not. × 12. Here $ \mathcal L_{\hat v}^{\{j\}} (z)$ denotes the $ j^{th}$ iterated $ \hat v$-directional derivative of the function $ z$.Given a traversally generic (see Definition 5.1) vector field $ v$ on a compact connected surface $ X$, we will attach the combinatorial pattern $ (11)$ to typical $ v$-trajectory $ \g \subset X$ that correspond to points in the interior of an edge of the graph $ \mathcal T(v)$, the pattern $ (121)$ to the trajectories that correspond to the trivalent verticies of $ \mathcal T(v)$, and the pattern $ (2)$ to the univalent verticies (see Fig. 5). In fact, the numbers 1 and 2 in these patterns reflect the order of tangency of the curves $ \hat\g$ and $ \d X$ at the points of $ \g \cap \d X$ (see Definition 7.1).
On a given compact surface $ X$, for traversally generic vector fields $ v$ no other patterns (say, like $ (1221)$ or $ (13)$) occur. In $ 2D$, this conclusion follows from Definition 5.1.
The lemma below is another way to state this fact. Its proof, relying on the Malgrange Preparation Theorem [Malgrange1964], can be found in [Katz2014b], Lemma 3.4.
Lemma 7.1.
Let $ v$ be a traversally generic vector field on $ X$. Extend $ (X, v)$ to a pair $ (\hat X, \hat v)$. In the vicinity of each $ v$-trajectory $ \g$, there exist special local coordinates $ (u, x)$ in $ \hat X$ and a real polynomial $ P(u, x)$ of degree $ 2$ or $ 4$ such that:- each $ \hat v$-trajectory is given by the equation $ \{x = const\}$,
- the boundary $ \d X$ is given by the polynomial equation $ \{P(u, x) = 0\}$,
- $ X$ is given by the polynomial inequality $ \{P(u, x) \leq 0\}$.
The polynomial $ P(u, x)$ takes three canonical forms:
- (1) $ u(u -1)$, which corresponds to the combinatorial pattern $ \mathbf{(11)}$,
- (2) $ u^2 - x,$ which corresponds to the combinatorial pattern $ \mathbf{(2)}$,
- (3) $ u\big((u -1)^2 + x\big)(u -2),$ which corresponds to the pattern $ \mathbf{(121)}$.
To summarize, at $ \d_2X(v)$ the order of tangency is $ 2$; the trajectories through $ \d_2^+X(v)$ have the combinatorial tangency pattern $ (121)$, and through $ \d_2^-X(v)$ the combinatorial tangency pattern $ (2)$. The rest of trajectories have the pattern $ (11)$.
We denote by $ \Omega^\bullet_{'\langle 1]}$ the partially ordered set whose elements are $ (11), (2), (121)$ and the order is defined by $ (11) \succ (2)$ and $ (11) \succ (121)$. This combinatorics does not look impressive. However, in higher dimensions, traversally generic vector fields on $ (n+1)$-manifolds with boundary generate a rich partially ordered finite list $ \Omega^\bullet_{'\langle n]}$ of combinatorial tangency patters. The poset $ \Omega^\bullet_{'\langle n]}$ is universal in each dimension $ n+1$. It is discussed in [Katz2016a].
8. Holography of Traversing Flows on
Surfaces

Let $ v$ be a traversally generic (see Definition 5.1) vector field on a compact connected surface $ X$ with boundary. In Sect. 1, we have introduced the causality map \begin{eqnarray*} C_v: \d_1^+X(v) \to \d_1^-X(v). \end{eqnarray*} It is a distant relative of the classical Poincaré Return Map [e.g., see [Teschi2012]] In the forthcoming paper we will see that, for the geodesic flows $ v^g$ on the tangent spherical bundle $ SM \to M$ over a smooth connected Riemannian $ n$-manifold $ (M, g)$ with boundary, $ C_{v^g}$ is the scattering map , a version of the billiard map . × 13.
Alternatively, one can think of $ C_v$ as determining a partial order "$ x \prec C_v(x)$" among the points $ x$ of the boundary $ \d X$.
The word "causality" in the name of $ C_v$ is motivated by the following pivotal special case.
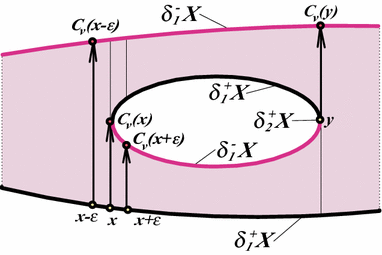
Example 8.1.
Let $ w = w(\theta, t)$ be a smooth time-dependent vector field on the circle $ S^1$ (equipped with the angular coordinate $ \theta$). It gives rise to a vector field $ v = (w, 1)$ on the cylinder $ S^1 \times \R$. We think about the factor $ S^1$ as space and about the factor $ \R$ as time . We denote by $ t$ the time coordinate. So we call $ S^1 \times \R$ the space of events . Note that $ v$ is a non-vanishing gradient-like vector field with respect to the time function $ T\colon S^1 \times \R \to \R$.Pick any smooth compact surface $ X \subset S^1 \times \R$ with a boundary $ \d X$. We call $ X$ the event domain , and its boundary $ \d X$ the event horizon .
Since the non-vanishing vector field $ v$ is traversing in $ X$, the map $ C_v$ is well-defined. Then the map $ C_v\colon \d_1^+X(v) \to \d_1^-X(v)$ indeed gives rise the causality relation on the event horizon: the correspondence $ C_v$ reflects the evolution of an event $ z = (\theta, t)$ into the event $ C_v(z)$.
Let $ \mathcal C(\d_2^+X(v))$ denotes the union of $ v$-trajectories through the points of the concavity locus $ \d_2^+X(v)$. The causality map is discontinuous at the points of the intersection $ \mathcal C(\d_2^+X(v)) \cap \d_1^+X(v)$ (see Fig. 7). On the positive side, the discontinuities of the causality map $ C_v$ are not too bad: the map has the "left" and "right" limits.
Given a pair $ (X, v)$, the $ v$-trajectories, viewed as un parametrized $ v$-oriented curves, produce an oriented $ 1$-dimensional foliation $ \mathcal F(v)$ on $ X$.
Theorem 8.1.
(The Causal Holography Principle in 2D)Let $ (X_1, v_1)$ and $ (X_2, v_2)$ be two compact connected surfaces with boundaries, carrying traversally generic vector fields $ v_1$ and $ v_2$, respectively. Assume that there is a diffeomorphism $ \Phi^\d\colon \d X_1 \to \d X_2$ which conjugates the two causality maps: \begin{eqnarray*} C_{v_2} \circ \Phi^\d = \Phi^\d \circ C_{v_1}. \end{eqnarray*}
Then $ \Phi^\d$ extends to a diffeomorphism $ \Phi\colon X_1 \to X_2$ which maps the oriented foliation $ \mathcal F(v_1)$ to the oriented foliation $ \mathcal F(v_2)$.
Proof.
We will only sketch the argument. A fully developed proof of the multidimensional analogue of this theorem is contained in [Katz2014c].First, we notice that since $ C_{v_1}$ and $ C_{v_2}$ are $ \Phi^\d$-conjugate, the diffeomorphism $ \Phi^\d$ induces a well-defined continuous map $ \Phi_{\mathcal T}\colon \mathcal T(v_1) \to \mathcal T(v_2)$ of the trajectory spaces. Moreover, $ \Phi_{\mathcal T}$ preserves the stratifications of the two trajectory spaces/graphs by the combinatorial type of trajectories. That is, the trivalent verticies of $ \mathcal T(v_1)$ are mapped to the trivalent verticies of $ \mathcal T(v_2)$, the univalent verticies are mapped to univalent verticies, and the interior of the edges to the interior of the edges.
Then we pick a smooth function $ f_2\colon X_2 \to \R$ such that $ df_2(v_2) > 0$. With the help of $ \Phi^\d$, we pull-back $ f_2|_{\d X_2}$ to get a smooth function $ f_1^\d\colon \d X_1 \to \R$ such that \begin{eqnarray*} f_1^\d(z) < f_1^\d(C_{v_1}(z)) \end{eqnarray*} for all $ z \in \d_1^+X_1(v_1)$.
Then we argue that $ f_1^\d$ extends to a smooth function $ f_1\colon X_1 \to \R$ such that $ df_1(v_1) > 0$.
We use $ f_1$ to embed $ X_1$ in the product $ \mathcal T(v_1) \times \R$ by the formula \begin{eqnarray*} \a_{\{v_1,\, f_1\}}(z) = (\g_z, f_1(z)), \end{eqnarray*} where $ \g_z$, the $ v_1$-trajectory through $ z$, is viewed as the point $ \Gamma_1(z)$ of the graph $ \mathcal T(v_1)$. Similarly, we use $ f_2$ to embed the surface $ X_2$ in the product $ \mathcal T(v_2) \times \R$ with the help of the map $ \a_{\{v_2, f_2\}}$.
Finally, we employ $ \Phi_{\mathcal T}$, $ f_1$ and $ f_2$ to construct a map \begin{eqnarray*} \hat \Phi: \mathcal T(v_1) \times \R \to \mathcal T(v_2) \times \R \end{eqnarray*} by the formula \begin{eqnarray*} \hat\Phi(\g, t) = \big(\Phi_{\mathcal T}(\g),\, f_1(f_2^{-1}(t))\big), \end{eqnarray*} where $ t$ belongs to the $ f_2$-image of the trajectory $ \Gamma_2^{-1}\big(\Phi_{\mathcal T}(\g)\big)$.
Crudely, the restriction of $ \hat\Phi$ to $ \a_{\{v_1,\, f_1\}}(X_1) \subset \mathcal T(v_1) \times \R$ is the desired diffeomorphism $ \Phi\colon X_1 \to X_2$.
Note that, in general, the image $ \Phi_\ast(v_1)$ is not $ v_2$; so the parametrizations of the trajectories are not respected by the diffeomorphism $ \Phi$, but the oriented $ 1$-foliations $ \mathcal F(v_1)$ and $ \mathcal F(v_2)$ are. ⬜
Theorem 8.1 leads instantly to the following corollary, stated as Theorem 1.3 in the introduction:
Corollary 8.1.
Let $ X$ be a compact connected surface with boundary, and $ v$ a smooth traversally generic vector field on it.Then the knowledge of the causality map $ C_v\colon \d_1^+X(v) \to \d_1^-X(v)$ is sufficient for a reconstruction of the pair $ (X, \mathcal F(v))$, up to a diffeomorphism of $ X$ that is the identity on $ \d X$.
The world "holography" is present in the name of Theorem 8.1 since the surface $ X$ and the $ 2D$-dynamical system, produced by the $ v$-flow, are recorded on two $ 1$-dimensional screens, $ \d_1^+X(v)$ and $ \d_1^-X(v)$.
Theorem 8.1 and Corollary 8.1 are valid in any dimension ([Katz2014c]).
Example 8.2.
Let $ v$ be a traversally generic vector field on a connected surface $ X$ whose boundary $ \d X$ is a single loop. Then the boundary $ \d X$ is divided into $ q$ disjoint arcs $ a_1, \dots , a_q$ that form $ \d_1^+X(v)$ and $ q$ complementary arcs $ b_1, \ldots , b_q$ that form $ \d_1^-X(v)$. The causality map \begin{eqnarray*} C_v: \coprod_{i=1}^q a_i \; \to \; \coprod_{i=1}^q b_i \end{eqnarray*} can be represented by its graph $ G(C_v) \subset \prod_{i, j} a_i \times b_j$.The map $ C_v$ (the curve $ G(C_v)$) is discontinuous at exactly $ c^+(v)$ points in $ \coprod_{i=1}^q a_i $ that correspond to the points of the intersection $ \mathcal C(\d_2^+X(v)) \cap \d_1^+X(v)$. There the map $ C_v$ has distinct left and right limits.
According to the Corollary 8.1, the curve $ G(C_v) \subset \prod_{i, j} a_i \times b_j$ determines $ X$ and the un -parametrized dynamic of the $ v$-flow, up to a diffeomorphism $ \Phi\colon X \to X$ that is the identity on $ \d X$. Note that the number $ q$ alone is not sufficient even to determine the genus of the surface $ X$.
Revisiting Example 8.2, we get the following interpretation of Corollary 8.1:
Corollary 8.2.
For any smooth time-dependent vector field $ w$ on the circle $ S^1$, the causality relation on the event horizon $ \d X$ is sufficient for a reconstruction of the event domain $ X$ and the un-parametrized $ (w, 1)$-flow, up to a diffeomorphism of $ X$ that is the identity on $ \d X$.In order to interpret the causality map as the Poincaré return map [see [Teschi2012]] of a dynamic system, we need to leave the Flatland and to sail into $ 3$-dimensional world.
Let us recall briefly the notion of a geodesic flow . Consider a compact surface/manifold $ X$ with a Riemannian metric $ g$. We denote by $ SX$ the space of unit tangent vectors on $ X$. Given a point $ x \in X$ and a unit tangent vector $ v \in T_xX$, take the germ of the unique geodesic curve $ \g\colon (-\e, \e) \to X$ through $ x$ such that $ \g(0) = x$ and $ \dot\g(0) = v$. Then the pair $ (\g(t), \dot\g(t))$ is a path in $ SX$; its tangent vector $ v^g = (\dot\g, \ddot\g)$ belongs to the tangent space $ T_{(x, v)}(SX)$. The vector field $ v^g$ on $ SX$ is called the geodesic vector field , and the flow on $ SX$ it generates is called the geodesic flow .
The theory of billiards on connected Riemmanian surfaces $ (X, g)$ with boundary benefits from applying a $ 3$-dimensional version of the Causal Holography Theorem 8.1 to the geodesic flow $ v^g$ on the $ 3$-dimensional manifold $ SX$. See [Katz2014c] for some of these applications. In addition to geodesic billiards, they include the classic inverse geodesic scattering problems.
Let us outline how these applications work. When $ \d X$ is connected (i.e., is a circle), then $ \d(SX)$ is a $ 2$-torus. If the metric $ g$ on $ X$ is such that the geodesic flow $ v^g$ is gradient-like Such metrics form an open set in the space of all Riemannian metrics. × 14, then the causality (scattering) map $ C_{v^g}$ acts from the annulus $ \d_1^+SX(v^g)$ to the annulus $ \d_1^-SX(v^g)$. Both annuli can be identified via a diffeomorphism $ \tau\colon \d_1^-SX(v^g) \to \d_1^+SX(v^g)$ that reflects each tangent vector to $ X$ at a point of $ \d X$ with respect to the boundary $ \d X$. The composition $ B_{v^g} =_{\mathsf{def}} \tau \circ C_{v^g}$, called the billiard map , is a self-map of the annulus $ \d_1^+SX(v^g)$. The iterations of the billiard map $ B_{v^g}$ give rise to an interesting dynamics on the annulus, a focal point of many investigations.
In this context, the main open and challenging for us question is: For which Riemannian metrics $ g$ on $ X$, the knowledge of the scattering map $ C_{v^g}\colon \d_1^+SX(v^g) \to \d_1^-SX(v^g)$ (equivalently, of the billiard map) is sufficient for a reconstruction of $ g$, say, up to a scalar?
9. Convex Envelops and Characteristic
Classes of Traversing Flows

Let $ X$ be a compact surface/manifold with boundary and $ v$ a traversing vector field (see Definition 1.1). We have seen that, as a function of a point $ x \in X$, the $ v$-trajectory $ \g_x \subset X$ through $ x$ exhibits a discontinuous behavior in the vicinity of any concavity point $ x_0 \in \d_2^+X$. In order to get around this fundamental difficulty, we "envelop" the pair $ (X, v)$ into a pair $ (\hat X, \hat v)$, an ambient compact surface/manifold $ \hat X \supset X$ ($ \dim(\hat X) = \dim(X)$) and a traversing vector field $ \hat v$, such that (see also Definition 9.3):
- (1) $ \d \hat X$ is convex with respect to the $ \hat v$-flow on $ \hat X$,
- (2) $ \hat v|_X = v$,
- (3) the $ \hat v$-flow is traversally generic with respect to $ \d X$.
Not any pair $ (X, v)$ admits such convex envelop (see Lemma 9.1). However, when available, the convex envelop $ (\hat X, \hat v)$ simplifies the analysis of $ (X, v)$ greatly.
In this context, our ultimate goal is to study the pseudo-isotopies and bordisms of convex envelops, by organizing them into monoids and groups, respectively, and to compute these algebraic structures for an a priori prescribed set of combinatorial tangency patterns. For $ n$-dimensional flows, this goal will be achieved in the forthcoming paper ([Katz2016c]) and in a chapter from the book ([Katz2017]). Although in dimension two these structures are quite primitive, they are not completely trivial either.
Recall that, in the study of manifolds, the universal classifying spaces like Grassmanians play a pivotal role. In the category of convex envelops, the role of universal objects (of "the new Grassmanians") is played by various spaces of smooth functions $ f\colon \R \to \R$, whose zeros and their multiplicities are modeled after the real divisors of real polynomials. The topology of these functional spaces with constrained zero divisors is interesting on its own right. One kind of these functional spaces has been studied in depth by [Arnold1989] and [Vasiliev1994].
In [Katz2016c], we will compute the homology of these functional spaces in terms of quite rich and universal combinatorics. This is reminiscent to the role played by the Schubert calculus in depicting the characteristic classes of classical Grassmanians.
In somewhat similar spirit, we apply our understanding of the algebraic topology of the universal functional spaces with restricted zero divisors on the number line to the traversing flows on manifolds with boundary. In particular, in [Katz2016c], we will introduce a rich variety of characteristic classes of convex envelops. In turn, this will allow us to manufacture, in a systematic way, examples of traversing flows with certain a priori prescribed combinatorial tangency patters in relation to the boundary.
Recall that, for boundary generic $ 2$-dimensional traversing flows, no tangencies of orders $ \geq 3$ occur. In light of what has been outlined above, we should anticipate a link between traversally generic flows on surfaces and the spaces of smooth functions $ f\colon \R \to \R$ (or even polynomials) that have no zeros of multiplicities $ \geq 3$.
Let $ \mathcal F$ denote the space (in the $ C^\infty$-topology) of smooths functions $ f\colon \R \to \R$ that are identically $ 1$ outside of a compact interval (the interval depends on a particular function). Let $ \mathcal F_{< k}$ be its subspace, formed by functions that have zeros only of the multiplicities less than $ k$. In [Arnold1989], Arnold calls such functions " functions with moderate singularities ". One can prove that any function with moderate singularities can be represented as a polynomial times a smooth positive function [Katz2016c]. In particular, the zero set $ f^{-1}(0)$ is finite for each $ f \in \mathcal F_{< k}$.
An important theorem of Vassiliev [see [Vasiliev1994], Corollary on page 81 and The First and Second Main Theorems on pp. 78--79] describes the weak homotopy types of the spaces $ \mathcal F_{< k}$ for all $ k \geq 4$ and their homology types for all $ k \geq 3$. In particular, the homology of the space $ \mathcal F_{\leq 2} =_{\mathsf{def}} \mathcal F_{< 3}$ is isomorphic to the homology of $ \Omega S^2$, the space of loops on a $ 2$-sphere! On the other hand, Arnold proved that the fundamental group $ \pi_1(\mathcal F_{\leq 2}) \approx \Z$ ([Arnold1989]). Thus, $ H^1(\mathcal F_{\leq 2}; \Z) \approx \Z$. For the $ 2$-dimensional traversing flows, this fact allows to define characteristic classes $ \theta_\a$ of convex envelops $ \a\colon (X, v) \subset (\hat X, \hat v)$, which reside in $ H^1(\hat X; \Z)$.
Let $ \hat v$ be a boundary convex traversing vector field on an annulus $ A$. With the help of $ \hat v$, we can introduce a product structure $ A \approx S^1 \times [0, 1]$ so that the fibers of the projection $ \theta\colon A \to S^1$ are the $ \hat v$-trajectories.
Definition 9.1.
Consider a collection $ L$ of several smooth immersed loops in the annulus $ A$, which intersect and self-intersect transversally and do not have triple intersections.We say that a boundary convex traversing vector field $ \hat v$ on $ A$ is generic relative to $ L$, if no $ \hat v$-trajectory $ \g$ contains more than one point of self-intersection from $ L$ and no more than one point of simple tangency to $ L$, but not both.
For a given $ L$, by standard techniques of the singularity theory, we can find a perturbation of $ \hat v$ within the space $ \mathcal V_{\mathsf{trav}}(A)$ so that the perturbed vector field is generic with respect to $ L$ and still convex with respect to $ \d A$ ([Katz2014b]).
Since an immersion is a smooth map of manifolds whose differential has the trivial kernel, the immersions allow for a transfer of a given vector field on the target manifold to a vector field on the source manifold. The transfer of a non-vanishing vector field is a non-vanishing vector field.
Note that any orientable surface $ X$ admits an immersion $ \a: X \to A$ (or even in the plane $ \R^2$) (see Fig. 8). We will use this fact to pull-back to $ X$ traversing convex vector fields on the target space $ A$.
Definition 9.2.
Consider an immersion $ \a: X \to A$ of a given compact orientable surface $ X$ into an annulus $ A$, equipped with a traversal boundary convex ("radial") vector field $ \hat v$. We call such $ \a$ generic relative to $ \hat v$, if $ \hat v$ is generic relative to the curves $ \a(\d X)$ in the sense of Definition 9.1.Given a transversally generic vector field $ v$ on a connected compact surface $ X$, we call a map $ \a\colon (X, v) \to (A, \hat v)$ a convex quasi-envelop of $ (X, v)$ if there exists an immersion $ \a\colon X \to A$ which is generic relative to the radial vector field $ \hat v$ on $ A$, and $ v = \a^\ast(\hat v)$, the pull-back of $ \hat v$.
Given a boundary generic relative to $ \hat v$ immersion $ \a\colon X \to A$, the $ \a$-pullback (transfer) of the vector field $ \hat v$ defines a non-vanishing vector field $ v$ on $ X$. Since $ \a$ is an immersion, evidently the pull-back $ v$ is traversing on $ X$. Moreover, $ v$ is traversally generic in the sense of Definition 5.1, since no $ v$-trajectory $ \g$ has more than one point of simple tangency to $ \d X$.
Definition 9.3.
Let $ \a\colon X \subset A$ be a regular embedding of a given compact surface $ X$ into an annulus $ A$, carrying a traversal boundary convex vector field $ \hat v$. We denote by $ v$ the pull-back of $ \hat v$ under $ \a$. If $ \a$ is traversally generic relative to $ \hat v$, then we say that the pair $ (A, \hat v)$ is a convex envelop of $ (X, v)$.The existence of a convex envelop puts significant restrictions on the topology of $ X$: such orientable surfaces $ X$ do not have $ 1$-handles. In other words, they are disks with holes.
Lemma 9.1.
If a compact connected surface $ X$ with boundary has a pair of loops whose transversal intersection is a singleton, then no traversal flow on $ X$ admits a convex envelop. In other words, if a connected surface $ X$ with boundary has a handle, then no traversal flow on $ X$ can be convexly enveloped.Proof.
By Lemma 1.2, the space $ \hat X$ of a convex envelop is either a disk or an annulus, both surfaces residing in the plane. No two loops in the plane intersect transversally at a singleton. Thus, for surfaces with a handle, no convex envelops exist. ⬜To incorporate surfaces with handles into our constructions, we have introduced the notion of a convex quasi-envelop (Definition 9.2).
Now we are in position to explore a connection between immersions $ \a\colon (X, v) \to (A, \hat v)$ of a given surface $ X$ in the annulus $ A$, such that $ v = \a^\ast(\hat v)$ and $ \hat v$ is generic with respect to $ \a(\d X)$ on one hand, and loops in the functional spaces $ \mathcal F_{\leq 2}$ on the other.
Let $ \a(\d X)^\times$ denote the set of self-intersections of the curves forming the image $ \a(\d X)$. Let $ \a(\d X)^\circ$ denote the set $ \a(\d X){\setminus}\a(\d X)^\times$.
We associate an auxiliary smooth function $ z_\a\colon A \to \R$ with the curves $ \a(\d X)$, subject to the following properties:
- $ z_\a^{-1}(0) = \a(\d X),$
- 0 is the regular value of $ z_\a$ at the points of $ \a(\d X)^\circ,$
- in the vicinity of each crossing point $ a \in \a(\d X)^\times$, consider local coordinates $ (x_1, x_2)$ such that $ \{x_1 =0\}$ and $ \{x_2 =0\}$ define the two intersecting branches of $ \a(\d X)$; then locally $ z_\a = c\cdot x_1x_2$, where the constant $ c \neq 0$.
- $ z_\a =1$ in the vicinity of $ \d A$,
The sign of $ z_\a$ changes to the opposite, as a path crosses an arc from $ \a(\d X)^\circ$ transversally, thus providing a "checker board" coloring of the domains in $ A \setminus \a(\d X)$.
We denote by $ A^\circ$ the interior of the annulus $ A$. Let $ \phi\colon A^\circ \to \R$ be a smooth function so that $ d\phi(\hat v) > 0$ in $ A^\circ$ and $ \phi(\hat\g \cap A^\circ) = \R$ for all $ \hat v$--trajectories $ \hat\g$ in $ A$. Then, with the help of $ z_\a$ and $ \phi$, we get a map $ J_{z_\a}\colon \mathcal T(\hat v) \to \mathcal F_{\leq 2}$. We define the map $ J_{z_\a}$ by the formula
| \begin{eqnarray}\label{eq1.8} J_{z_\a}(\hat \g) = (z_\a|_{\hat \g}) \circ (\phi |_{\hat\g})^{-1}, \end{eqnarray} | (9.2) |
For a fixed $ \a$, it is easy to check that the homotopy class $ [J_{z_\a}]$ of $ J_{z_\a}$ does not depend on the choice of the auxiliary function $ z_\a$, subject to the four properties in (9.1). Indeed the space of such functions $ z_\a$ is convex and thus contractible.
We pick a generator $ \kappa \in \pi_1(\mathcal F_{\leq 2}) \approx \Z$ and define the integer $ J^\a$ by the formula $ J^\a \cdot \kappa = [J_{z_\a}]$. As a result, any immersion $ \a\colon X \to A$, which is generic with respect to $ \hat v$, produces a homotopy class $ [J_{z_\a}] \in \pi_1(\mathcal F_{\leq 2})$ and an integer $ J^\a$.
The isomorphism $ \pi_1(\mathcal F_{\leq 2}) \approx \Z$ follows from [Arnold1989] by a slight modification of the arguments there.
Let us start with the key observation in [Arnold1989]. Generic loops in $ \b\colon S^1 \to \mathcal F_{\leq 2}$ have an interpretation in terms of finite collections $ C$ of smooth closed curves in the annulus $ A$ with no inflection points with respect to their tangent lines of the form $ \{\theta = const\}$ in the $ (u, \theta)$-coordinates. We call such tangent lines $ \theta$- vertical . Furthermore, the generic homotopy between such loops $ \b$ corresponds to some cobordism relation between the corresponding plane curves, the cobordism also avoids the $ \theta$-vertical inflections.
First, let us spell out the genericity requirements on the collections $ C$ of closed curves in the annulus $ A$ (carrying the angular coordinate $ \theta$ and the radial coordinate $ u$):
- (1) $ C \subset A$ is a finite collection of closed smooth immersed curves $ \{C_j\}_j$,
- (2) the projections $ \{\theta\colon C_j \to S^1\}_j$ have the Morse type singularities only This allows for local maxima/minima only and excludes the $ \theta$-vertical inflections. × 15,
- (3) the self-intersections and mutual intersections of the curves $ \{C_j\}_j$ are transversal and no triple intersections are permited,
- (4) at each double intersection, the two banches of $ C$ are not parallel to the $ u$-coordinate,
- (5) the $ \theta$-images of the intersections and of the critical values of $ \{\theta\colon C_j \to S^1\}_j$ are all distinct in $ S^1$.
Definition 9.4.
Given two collections $ C_0$ and $ C_1$ of immersed closed curves as in (9.3), we say that they are cobordant with no $ \theta$ -vertical inflections , if there is a smooth function $ F: A \times [0, 1] \to \R$ such that:- $ 0$ is a regular value of $ F$,
- the restriction of the projection $ T: A \times [0, 1] \to [0, 1]$ to the zero set $ W =_{\mathsf{def}} F^{-1}(0)$ is a Morse function,
- $ C_0 = W \cap (A \times \{0\})$ and $ C_1 = W \cap (A \times \{1\})$,
- for each $ t \in [0, 1]$, the section $ C_t =_{\mathsf{def}} W \cap (A \times \{t\})$ has no $ \theta$-horizontal inflections Note that the second bullet excludes the triple intersections of $ C_t$. × 16.
It is possible to verify that the cobordism with no $ \theta$-vertical inflections is an equivalence relation among collections of curves as in (9.3). Indeed, if $ C$ is cobordant to $ C'$ with the help of $ F$, and $ C'$ to $ C''$ with the help of $ F'$, then there exists a piecewise smooth function $ F \cup F'\colon A \times [0, 2] \to \R$ whose restriction to $ A \times [0, 1]$ is $ F$ and to $ A \times [1, 2]$ is $ 1+ F'$. Smoothing $ F \cup F'$ along $ A \times \{1\}$ in the normal direction and scaling down the interval $ [0, 2]$ to $ [0,1]$, produces the desired function-cobordism $ F \ast F'\colon A \times [0, 1] \to \R$.
So we can talk about the set of bordisms $ \mathbf B_{\mathsf{no\, \theta-inflect.}}$, based on collections of closed curves in the annulus with no $ \theta$-vertical inflections. This set is a group : the operation $ C, C' \Rightarrow C \ast C'$ is defined by the union $ \tilde C \cup \tilde C' \subset A$, where $ \tilde C \subset S^1 \times (0, 0.5)$ and $ \tilde C' \subset S^1 \times (0.5, 1)$ are the images of $ C$ and $ C'$, scaled down in the $ u$-direction by the factor $ 0.5$ and placed in sub-annuli of $ A = S^1 \times [0, 1]$. The role of $ -C$ is played by the mirror image of $ C$ with respect to a vertical (equivalently, horizontal) line, a fiber of $ \theta\colon A \to S^1$.
Note that the operation $ \ast$ may affect the maximal cardinalities $ d$ and $ d'$ of the fibers $ \theta\colon C \to S^1$ and $ \theta: C' \to S^1$ in a somewhat unpredictable way. In any case, the fiber cardinality of $ \theta\colon C\ast C' \to S^1$ has the upper boundary $ d + d'$.
The previous constructions deliver the following slight modification of Theorem from [Arnold1989].
Theorem 9.1.
The fundamental group $ \pi_1(\mathcal F_{\leq 2})$ is isomorphic to the bordism group $ \mathbf B_{\mathsf{no\, \theta-inflect.}}$, based on finite collections of immersed loops with no $ \theta$-vertical inflections in the annulus $ A$ and subject to the constraints (9.3). The isomorphism is induced by the correspondence \begin{eqnarray*} K: \{\b: S^1 \to \mathcal F_{\leq 2}\}\; \Rightarrow \bigcup_{\theta \in [0, 2\pi]} (\theta, \beta(\theta)^{-1}(0)) \subset S^1 \times [0, 1]. \end{eqnarray*}This theorem is a foundation of a graphic calculus that converts homotopies of loops in the functional space $ \mathcal F_{\leq 2}$ into cobordisms of closed loop patterns with no $ \theta$-vertical inflections in the annulus $ A$. The reader may glance at Figs. 10--14 from [Katz2015] to get a feel how the calculus works. These figures explain why any loop in $ \mathcal F_{\leq 2}$ is homotopic to an integral multiple of a generator $ \kappa \in \pi_1(\mathcal F_{\leq 2})$, represented by a model loop pattern $ K \subset A$ as in Fig. 9, diagram (a) or (b).
Let us orient the annulus $ A = S^1 \times [0, 1]$ so that the the $ \theta$-coordinate, corresponding to $ S^1$, is the first, and the $ u$-coordinate, corresponding to $ [0, 1]$, is the second.
We fix an orientation of $ X$, thus picking orientations for each component of $ \d X$. Given an orientation-preserving immersion $ \a: (X, v) \to (A, \hat v)$ such that $ \a(\d X)$ has the properties as in (9.3), we assign the polarity "$ \oplus$" to a point $ a \in \d_2^+X(v)$ if $ \a_\ast(\nu_a)$ points in the direction of $ \theta$. Here where $ \nu_a$ is the inner normal to $ \d X$ at $ a$. Otherwise, the polarity of $ a \in \d_2^+X(v)$ is defined to be "$ \ominus$" (see Fig. 9). Thus, using new polarities, we get a partition $ \d_2^+X(v) = \d_2^{+, \oplus}X(v) \coprod \d_2^{+, \ominus}X(v)$.
Finally, we are in position to state the main result of Sect. 9. Its proof can be found in [Katz2015]. It is an application of the Arnold surgery calculus of loops with no $ \theta$-vertical inflections.
Theorem 9.2.
Any orientation-preserving immersion $ \a\colon (X, v) \to (A, \hat v)$, giving rise to a convex quasi-envelop, such that $ \hat v$ is generic with respect to $ \a(\d X)$, produces a map $ J_{z_\a}\colon S^1 \to \mathcal F_{\leq 2}$ (see ( (9.2) )). Its homotopy class $ [J_{z_\a}] = J^\a \cdot \kappa$, where $ \kappa$ denots a generator of $ \pi_1( \mathcal F_{\leq 2}) \approx \Z$.The integer $ J^\a$ can be computed by the formula: \begin{eqnarray*} J^\a = \#\{\d_2^{+, \oplus}X(v)\} - \#\{\d_2^{+, \ominus}X(v)\} \end{eqnarray*} and thus does not depend on $ \a$ (as long as the transfer $ \a^\ast(\hat v) = v$).
Moreover, $ |J^\a| \leq c_2^+(v)$, the complexity of the $ v$-flow.
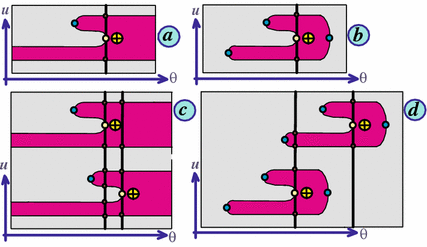
Remark 9.1.
It is interesting to notice that the invariant $ J^\a = \#\{\d_2^{+, \oplus}(v)\} - \#\{\d_2^{+, \ominus}(v)\}$ reflects more the topology of the vector field $ v= \a^\ast(\hat v)$ than the topology of the surface $ X$: in fact, any integral value of $ J^\a$ can be realized by a traversally generic vector field $ v$ on a $ 2$- disk $ D$ which even admits a convex envelop! A portion of the boundary $ \d D$ looks like a snake (see Fig. 9) with respect to the vector field $ \hat v$ of the envelop. For any $ X$, the effect of deforming a portion of $ \d X$ into a snake is equivalent to adding several times a spike (an edge and a pair of univalent and trivalent verticies) to the graph $ \mathcal T(v)$. Evidently, these operations do not affect $ H_1(\mathcal T(v); \Z) \approx H_1(X; \Z)$.In contrast, $ \#\{\d_2^{+, \oplus}(v)\} + \#\{\d_2^{+, \ominus}(v)\} \geq 2|\chi(X)|$ has a topological significance for $ X$.
For example, for $ \a$ as in Fig. 8, $ J^\a =0$. If we subject $ \a$ to an isotopy that introduces a snake-like pattern of Fig. 9a, then for the new immersion $ \a'$, the invariant $ J^{\a'} = 1$.
Remark 9.2.
Consider a connected oriented surface $ X$ with a connected boundary. (We exclude the case of a $ 2$-disk.) It is a boundary connected sum of a few copies of $ T^\circ$, the torus with a hole. A punctured torus admits an immersion $ \a\colon T^\circ \to A$ in the annulus so that the cardinality of the fibers of $ \theta: \a(\d T^\circ) \to S^1$ does not exceed $ 6$ (see Fig. 8). Therefore, any connected oriented surface $ X$ with boundary admits an immersion $ \a\colon X \to A$ with the property $ \#\{ \theta^{-1}(\theta_\star) \cap \a(\d X)\} \leq 6$ for all $ \theta_\star \in S^1$.Any $ \hat v$-generic immersion $ \a\colon X \to A$ also produces a well-defined element $ [K_\a]$ in the set of homotopy classes $ [\mathcal T(v), \mathcal F_{\leq 2}]$ of maps from the trajectory graph $ \mathcal T(v)$ to the functional space $ \mathcal F_{\leq 2}$. Its construction is similar to the one of $ J_{z(\a)}$. Consider the $ \hat v$-generated obvious map $ Q_\a\colon \mathcal T(v) \to \mathcal T(\hat v) \approx S^1$ (each $ v$-trajectory is contained in the unique $ \hat v$-trajectory). Put $ K_\a =_{\mathsf{def}} J_{z(\a)} \circ Q_\a$.
Remark 9.3.
Note that, for some immersions $ \a\colon X \to A$, the invariant $ J^\a$ may be different from $ 0$, but $ [K_\a]$ may be trivial. For example, this is the case when $ X$ is a disk with a snake-like boundary $ \a(\d X)$ with respect to $ \hat v$. However, there exist immersions $ \a$ with a nontrivial $ [K_\a]$. For example, such is the immersion in [Katz2015], Figure 10, (1). At the same time, for $ \a$ in [Katz2015], Figure 11, (3), $ [K_\a]$ is trivial.Since $ \pi_1(\mathcal F_{\leq 2}) \approx \Z$, it follows that $ H_1(\mathcal F_{\leq 2}; \Z) \approx \Z$. In turn, this implies that the $ 1$-dimensional cohomology $ H^1(\mathcal F_{\leq 2}; \Z) \approx \Z$. Thus $ K_\a$ induces a homomorphism \begin{eqnarray*} K_\a^\ast: H^1(\mathcal F_{\leq 2}; \Z) \to H^1(\mathcal T(v); \Z) \approx H^1(X; \Z). \end{eqnarray*} In particular, we get an element $ K_\a^\ast(\kappa) \in H^1(X; \Z)$, where $ \kappa$ is a generator of $ H^1(\mathcal F_{\leq 2}; \Z) \approx \Z$. $ K_\a^\ast(\kappa)$ is a characteristic cohomology class of the given $ \hat v$- generic immersion $ \a$. It is an invariant of the class $ [\a] \in \mathbf B_{\mathsf{no\, \theta-inflect.}}$.
Theorem 9.2 implies that, if two $ \hat v$-generic immersions $ \a_1, \a_2: X \to A$ are such that the pull-backs $ \a_1^\ast(\hat v) = \a^\ast_2(\hat v) = v$, then $ K_{\a_1}^\ast(\kappa) = K_{\a_2}^\ast(\kappa)$.
So the cohomology class $ K_\a^\ast(\kappa)$ turns out to be a characteristic class of $ v$! It is desirable to be able to reach this conclusion without relying on the cobordisms of curves' patterns in $ A$ with no $ \theta$-vertical inflections.
The space $ \mathcal F_{\geq 3}$ has codimension $ 2$ in $ \mathcal F$; so a loop in $ \mathcal F$ may be linked with $ \mathcal F_{\geq 3}$. In fact, the value of $ K_\a^\ast(\kappa)$ on any loop ($ 1$-cycle) $ \delta\colon S^1 \to X$ equals to the linking number $ \mathsf{lk}(K_\a(\delta), \mathcal F_{\geq 3})$. The validation of this claim and of its generalizations will appear in [Katz2016c], [Katz2017].
In dimensions higher than two, similar considerations apply to produce characteristic classes of traversally generic flows. They are based on quite involved computations of homology of spaces of real monic polynomials with restricted combinatorics of their real divisors.
As a result of these computations, it turns out that the topology of high-dimensional convex envelops is at least as intricate as the homotopy groups of spheres [Katz2016c].
10. A Glance at the $ 3D$-Lands

Here is brief overview of how some elements of our program manifest themselves in dimension three.
Let $ v$ be a traversally generic (see Definition 5.1 for the $ 2D$-flows and its generalization in [Katz2009], [Katz2014b] for the $ n$-dimensional flows) vector field on a compact connected $ 3$-dimensional manifold $ X$ with boundary. The trajectories of such vector fields have the combinatorial tangency patterns from the poset $ \Omega^\bullet_{'\langle 2]} = \{(11);\, (2), (121);\, (1221), (31), (13)\}$.
Consider the number $ gc(v)$ of $ v$-trajectories that are simply tangent (have tangency of order $ 2$ in the sense of Definition 7.1) to the boundary $ \d X$ at two distinct points. We call this number $ gc(v)$ the gradient complexity of $ v$. It is an example of an invariant of the vector field $ v$, considered up to the natural action of diffeomorphism group $ \mathsf{Diff}(X)$ on vector fields. We minimize $ gc(v)$ over all traversally generic vector fields on $ X$ to produce the gradient complexity $ gc(X)$, a new invariant of $ X$.
Recall that any compact $ 3$-manifold can be assembled out of the standard building blocks (in technical terms, these blocks are "boundary irreducible" with no "essential annuli" compact $ 3$-manifolds) by gluing them along their boundary components [Jaco and Shalen1979]. It turns out that there exist only finitely many standard blocks whose gradient complexity $ gc(\sim)$ is bounded from above ([Katz2009], Theorem 7.3).
Let $ Y$ be a closed hyperbolic $ 3$-manifold, and let $ X$ be obtained by removing a $ 3$-ball from $ Y$. In [Katz2009], Theorem 7.5, we prove that the gradient complexity of $ X$ is greater than or equal to the normalized hyperbolic volume of $ Y$. In fact, this type of result is valid in any dimension ([Alpert and Katz2015], Theorem 1). In particular, compare this claim with Theorem 4.1, the $ 2$-dimensional analogue.
Our investigation of vector flows in Flatland has reached its conclusion. To find out how things flow in other lands---"the romances of many dimensions"---([Abbott1992]), the reader could consult with the references below.
Acknowledgements.
We are grateful to the referees; their thoughtful and detailed recommendations helped to improve the quality of our presentation.References
[Alpert and Katz2015] Alpert, H., Katz, G.: Using simplicial volume to count multi-tangent trajectories of traversing vector fields. Geometriae Dedicata 180 (1), 323--338 (2015)
[Arnold1989] Arnold, V.I.: Spaces of functions with moderate singularities, Func. Analysis & Its Applications, 23(3):1--10 (1989) (Russ)
[Barannikov1994] Barannikov, S.A.: The framed Morse complex and its invariants, Advances in Soviet Mathematics, Vol. 21, V. I. Arnold Ed., 93115 (1994)
[Cohen1991] Cohen R.L.: Topics in Morse theory Stanford University (1991)
[Goresky and MacPherson1983a] Goresky, M., MacPherson, R.: Stratified Morse Theory. Proceedings of Symposia in Pure Mathematics 40(Part 1):517--533 (1983a)
[Goresky and MacPherson1983b] Goresky, M., MacPherson, R.: Morse theory for the intersection homology groups, Analyse et Topologie sur les Espaces Singulieres, Astérisque #101 (1983b), 135--192, Société Mathématique de France
[Goresky and MacPherson1989] Goresky, M., MacPherson, R.: Theory, Stratified Morse, Springer Verlag, N.Y.: Ergebnisse, vol. 14. Also translated into Russian and published by MIR Press, Moscow (1989). 1991
[Gottlieb1996] Gottlieb, D.H.: All the way with Gauss-Bonnet and the sociology of mathematics. Math. Monthly 103 , 457--469 (1996)
[Gromov1982] Gromov, M.: Volume and bounded cohomology. Publ. Math. I.H.E.S., tome 56:5--99 (1982)
[Guth2009] Guth, L.: Minimal number of self-intersections of the boundary of an immersed surface in the plane. arXiv:0903.3112v1 [math.DG] (2009)
[Hardon2004] Hardon, D.G.C.: The Morse Complex for a Morse Function on a Manifold with Corners. arXiv:math.GT/0406486v1 (2004)
[Hopf1937] Hopf, H.: Vectorfelder in $ n$-dimensionalen Mannigfaltigkeiten. Math. Annalen 96 , 225--250 (1937)
[Jaco and Shalen1979] Jaco, W.H., Shalen, P.B.: Seifert fibered spaces in 3- manifolds. Mem. Am. Math. Soc. 21(220) (1979)
[Katz2009] Katz, G.: Convexity of Morse Stratifications and gradient spines of 3-manifolds. JP J. Geometry Topol. 9 (1), 1--119 (2009)
[Katz2014a] Katz,G.: Stratified Convexity and Concavity of Gradient Flows on Manifolds with Boundary. Appl. Math. 5 , 2823--2848 (2014a). (also arXiv:1406.6907v1 [mathGT]
[Katz2014b] Katz, G.: Traversally Generic and Versal Flows: Semi-algebraic Models of Tangency to the Boundary. Asian J. Math. (2014b, to appear). arXiv:1407.1345v1 [mathGT]
[Katz2014c] Katz, G.: Causal Holography of Traversing Flows (2014c). arXiv:1409.0588v1 [mathGT]
[Katz2015] Katz, G.: Flows in Flatland: a Romance of few Dimensions (2015). arXiv:1511.03310v2 [math.GT]
[Katz2016a] Katz, G.: The Stratified Spaces of Real Polynomials and Trajectory Spaces of Traversing Flows. JP J. Geometry Topol. 19 (2), 95--160 (2016a). arXiv:1407.2984v3 [math.GT]
[Katz2016b] Katz, G.: Complexity of Shadows and Traversing Flows in Terms of the Simplicial Volume. J. Topol. Anal. 8 (3), 501--543 (2016b). arXiv:1503.09131v2 [mathGT]
[Katz2016c] Katz, G.: Spaces of Functions with Constrained Zero Divisors, Convex Envelops of Traversing Flows, and their Characteristic Classes, manuscript (2016c)
[Katz2017] Katz, G.: Morse Theory, Gradient Flows, Concavity, and Complexity on Manifolds with Boundary, monograph. World Sci. (2017)
[Laudenbach2011] Laudenbach, F.: Morse Complex on Manifolds with Boundary. Geom. Dedicata 153 , 47--57 (2011)
[Malgrange1964] Malgrange, B.: The preparation theorem for differential functions. Differential Analysis (Papers presented at the Bombay Colloquium), pp. 203--208 (1964)
[Milnor1965] Milnor, J.: Morse Theory. Princeton University Press, Princeton (1965)
[Morse1929] Morse, M.: Singular points of vector fields under general boundary conditions. Am. J. Math. 51 , 165--178 (1929)
[Morse and Van Schaack1934] Morse, M., Van Schaack, G.B.: The critical point theory under general boundary conditions. Ann. Math. (2) 35(3):545571 (1934)
[Teschi2012] Teschi, G.: Ordinary differential equations and dynamical systems. Graduate Studies in Math., 140, AMS publication (2012)
[Vasiliev1994] Vasiliev, V.A.: Complements of Discriminants of Smooth Maps: Topology and Applications, Translations of Mathematical Monographs, vol. 98. Society publication, American Math (1994)
[Whitney1937] Whitney, H.: On regular closed curves in the plane. Comp. Math. 4 , 276--284 (1937)
- 99
- × Abbott, E.: Flatland: A romance of many dimensions. Dover Publications, New York (1992)
- × Alpert, H., Katz, G.: Using simplicial volume to count multi-tangent trajectories of traversing vector fields. Geometriae Dedicata 180 (1), 323--338 (2015)
- × Arnold, V.I.: Spaces of functions with moderate singularities, Func. Analysis & Its Applications, 23(3):1--10 (1989) (Russ)
- × Barannikov, S.A.: The framed Morse complex and its invariants, Advances in Soviet Mathematics, Vol. 21, V. I. Arnold Ed., 93115 (1994)
- × Cohen R.L.: Topics in Morse theory Stanford University (1991)
- × Goresky, M., MacPherson, R.: Stratified Morse Theory. Proceedings of Symposia in Pure Mathematics 40(Part 1):517--533 (1983a)
- × Goresky, M., MacPherson, R.: Morse theory for the intersection homology groups, Analyse et Topologie sur les Espaces Singulieres, Astérisque #101 (1983b), 135--192, Société Mathématique de France
- × Goresky, M., MacPherson, R.: Theory, Stratified Morse, Springer Verlag, N.Y.: Ergebnisse, vol. 14. Also translated into Russian and published by MIR Press, Moscow (1989). 1991
- × Gottlieb, D.H.: All the way with Gauss-Bonnet and the sociology of mathematics. Math. Monthly 103 , 457--469 (1996)
- × Gromov, M.: Volume and bounded cohomology. Publ. Math. I.H.E.S., tome 56:5--99 (1982)
- × Guth, L.: Minimal number of self-intersections of the boundary of an immersed surface in the plane. arXiv:0903.3112v1 [math.DG] (2009)
- × Hardon, D.G.C.: The Morse Complex for a Morse Function on a Manifold with Corners. arXiv:math.GT/0406486v1 (2004)
- × Hopf, H.: Vectorfelder in $ n$-dimensionalen Mannigfaltigkeiten. Math. Annalen 96 , 225--250 (1937)
- × Jaco, W.H., Shalen, P.B.: Seifert fibered spaces in 3-manifolds. Mem. Am. Math. Soc. 21(220) (1979)
- × Katz, G.: Convexity of Morse Stratifications and gradient spines of 3-manifolds. JP J. Geometry Topol. 9 (1), 1--119 (2009)
- × Katz,G.: Stratified Convexity and Concavity of Gradient Flows on Manifolds with Boundary. Appl. Math. 5 , 2823--2848 (2014a). (also arXiv:1406.6907v1 [mathGT]
- × Katz, G.: Traversally Generic and Versal Flows: Semi-algebraic Models of Tangency to the Boundary. Asian J. Math. (2014b, to appear). arXiv:1407.1345v1 [mathGT]
- × Katz, G.: Causal Holography of Traversing Flows (2014c). arXiv:1409.0588v1 [mathGT]
- × Katz, G.: Flows in Flatland: a Romance of few Dimensions (2015). arXiv:1511.03310v2 [math.GT]
- × Katz, G.: The Stratified Spaces of Real Polynomials and Trajectory Spaces of Traversing Flows. JP J. Geometry Topol. 19 (2), 95--160 (2016a). arXiv:1407.2984v3 [math.GT]
- × Katz, G.: Complexity of Shadows and Traversing Flows in Terms of the Simplicial Volume. J. Topol. Anal. 8 (3), 501--543 (2016b). arXiv:1503.09131v2 [mathGT]
- × Katz, G.: Spaces of Functions with Constrained Zero Divisors, Convex Envelops of Traversing Flows, and their Characteristic Classes, manuscript (2016c)
- × Katz, G.: Morse Theory, Gradient Flows, Concavity, and Complexity on Manifolds with Boundary, monograph. World Sci. (2017)
- × Laudenbach, F.: Morse Complex on Manifolds with Boundary. Geom. Dedicata 153 , 47--57 (2011)
- × Malgrange, B.: The preparation theorem for differential functions. Differential Analysis (Papers presented at the Bombay Colloquium), pp. 203--208 (1964)
- × Milnor, J.: Morse Theory. Princeton University Press, Princeton (1965)
- × Morse, M.: Singular points of vector fields under general boundary conditions. Am. J. Math. 51 , 165--178 (1929)
- × Morse, M., Van Schaack, G.B.: The critical point theory under general boundary conditions. Ann. Math. (2) 35(3):545571 (1934)
- × Teschi, G.: Ordinary differential equations and dynamical systems. Graduate Studies in Math., 140, AMS publication (2012)
- × Vasiliev, V.A.: Complements of Discriminants of Smooth Maps: Topology and Applications, Translations of Mathematical Monographs, vol. 98. Society publication, American Math (1994)
- × Whitney, H.: On regular closed curves in the plane. Comp. Math. 4 , 276--284 (1937)