Received: 4 February 2016 / Revised: 30 November 2016 / Accepted: 23 December 2016
Department of Mathematics,
Northwestern University,
Evanston IL 60208 USA and Kathryn Lindsey klindsey@math.uchicago.edu
Department of Mathematics,
University of Chicago,
Chicago IL 60637 USA
Abstract
Keywords
Julia set, Convex shape, Polyhedra, Harmonicmeasure, Curvature
1. Introduction

A planar shape is a compact, connected subset of the Euclidean plane that contains at least two points and has connected complement. Given a probability measure $ \mu$ supported on the boundary of a planar shape $ P$, we investigate the existence of a conformal metric $ \rho = \rho(z) |dz|$ on the Riemann sphere $ \Chat$ so that
- (i) $ P$, with its Euclidean metric from $ \R^2$, embeds locally-isometrically into $ (\Chat, \rho)$; and
- (ii) the curvature distribution $ \omega_\rho = -\Delta \log \rho(z)$ on $ \Chat$ is equal to the push-forward of $ 4\pi \mu$ under the embedding.
Alexandrov's theorems on convex surfaces ([Alexandroff1942], [Aleksandrov1948], [Alexandrov2005]) assert that any abstract metrized sphere with non-negative curvature is isometric to the boundary surface of a convex body in $ \mathbb{R}^3$ with its induced metric (unique up to rigid motions of $ \mathbb{R}^3$). In particular, the metrized sphere $ (\Chat, \rho(P,\mu))$ will have a unique convex 3D realization. The convex body may be degenerate , meaning that it lies in a plane and the sphere is viewed as the double of a convex planar region. Conversely, the surface of any compact, convex body in $ \R^3$ (not contained in a line) may be endowed with a complex structure and uniformized so that it is isometric to the Riemann sphere with a conformal metric of non-negative curvature; see, e.g. [Reshetnyak1993]. Thus, the existence of $ \rho(P,\mu)$ may be viewed as a problem of "folding" the shape $ P$ into $ \R^3$ and taking its convex hull, in such a way that the curvature of the resulting convex body is given by $ 4\pi \mu$.
The complement of $ P$ in $ (\Chat, \rho(P,\mu))$ will be called the cap of $ (P, \mu)$ and denoted by $ \hat{P}_\mu$. By construction, the metric on the cap is flat, so there is a locally isometric development map \begin{eqnarray*} D: \hat{P}_\mu \to (\Cak, |dz|). \end{eqnarray*} We say the cap is planar if the development $ D$ is injective.
Our first observation is that there always exists a probability measure $ \mu$ supported on $ \del P$ so that the metric $ \rho(P,\mu)$ exists (see Sect. 2.1 for a simple but degenerate construction). We also observe that not all caps are planar, and we give examples in Sect. 2.
The harmonic cap. We are especially interested in the case where $ P$ is a connected filled Julia set $ K(f)$ of a polynomial $ f: \Cak\to\Cak$ and the prescribed measure $ \mu$ is the measure of maximal entropy supported on the boundary of $ K(f)$; see details in Sect. 2.4. This metrized sphere was defined in ([DeMarco2003], Section 12) for an arbitrary rational map $ f: \P^1 \to \P^1$ of degree $ >1$. Questions about the features of its 3-dimensional realization were first posed by McMullen and Thurston.
To this end, we examine arbitrary planar shapes $ P\subset \Cak$, and we let $ \mu$ be the harmonic measure for the domain $ \Chat{\setminus} P$ relative to $ \infty$. By definition, $ \mu$ is the push-forward of the Lebesgue measure on the unit circle $ S^1$ (normalized to have total mass 1) under a conformal isomorphism $ \Phi : \Cak{\setminus} \overline{\D} \to \Cak{\setminus} P$; the measure $ \mu$ is well defined even if $ \Phi$ is not everywhere defined on $ S^1$. In this setting, the metric $ \rho(P,\mu)$ is simply an extension of the Euclidean metric $ |dz|$ on $ P$; it can be expressed in terms of the Green function \begin{eqnarray*} G_P(z) = \log|\Phi^{-1}(z)| \end{eqnarray*} for $ z \in \Cak{\setminus} P$. Setting $ G_P(z) = 0$ for $ z\in P$, we have \begin{eqnarray*} \rho(P,\mu) = e^{-2G_P(z)}|dz|. \end{eqnarray*} Observe that the metric $ \rho(P,\mu)$ is continuous on all of $ \Chat$: $ G_P$ is continuous on $ \Cak$ (by solvability of the Dirichlet problem on simply-connected domains), and it grows as $ \gamma + \log|z| + o(1)$ as $ z\to\infty$ for some $ \gamma\in\R$. The cap $ \hat{P}_\mu$ is called the harmonic cap of $ P$.
Theorem 1.1.
Let $ P$ be any planar shape and let $ \mu$ be the harmonic measure on $ \del P$, relative to $ \infty$. Let $ \Phi : \Chat{\setminus} \overline{\D} \to \Chat{\setminus} P$ be a conformal isomorphism with $ \Phi(\infty) = \infty$. A Euclidean development of the harmonic cap $ \hat{P}_\mu$ is given by the locally univalent function $ g: \D\to\Cak$ defined by \begin{eqnarray*} g(z) = \int_0^z \Phi'(1/x) \, dx. \end{eqnarray*} Moreover, there exist planar shapes $ P$ for which the harmonic cap is not planar.Theorem 1.1 allows one to appeal to the theory of univalent functions for conditions on $ P$ that guarantee planarity of the harmonic cap. If the harmonic cap is planar, then the construction can be iterated, to find the harmonic cap of the development of a harmonic cap. It would be interesting to understand the properties of this dynamical system on a class of planar shapes. (The closed unit disk is a fixed point of this operation; see Example 4.1.)
Constructing a cap. Given the data of a conformal metric $ (\Chat, \rho)$ with non-negative curvature distribution, it is a notoriously difficult problem to construct the 3D realization, even for polyhedral metrics (as we discuss below). But it turns out that a development of a cap $ \hat{P}_\mu$ in $ \Cak$ can be easily produced on the computer.
For planar shapes that are Jordan domains with rectifiable boundaries, a cap $ \hat{P}_\mu$ will have boundary of the same length as $ \del P$. A perimeter gluing of $ P$ and $ \hat{P}_\mu$ is the boundary identification (by arclength) between $ \del P$ and $ \del \hat{P}_\mu$ that produces $ (\Chat, \rho(P,\mu))$.
Theorem 1.2.
Let $ P$ be a planar shape with a piecewise-differentiable Jordan curve boundary, and let $ \mu$ be a nonnegative Borel probability measure supported on the boundary of $ P$. Let $ s$ be a counterclockwise, unit-speed parametrization of $ \partial P$, and write $ s(t) = \int_0^t e^{i\alpha(x)} \, dx$ for a real-valued function $ \alpha$. If the cap $ \hat{P}_\mu$ exists, then the boundary of its Euclidean development is parameterized in the clockwise direction by \begin{eqnarray*} \hat{s}(t) = \int_0^t e^{i (\alpha(x) - \kappa(x))} \, dx \end{eqnarray*} where $ \kappa(t) = 4\pi \mu(s(0,t])$, and the perimeter gluing is given by $ s(t) \sim \hat{s}(t)$, .Given an arbitrary planar shape $ P$, we can approximate it by a shape $ P'$ with piecewise-differentiable Jordan curve boundary and approximate any given measure $ \mu$ on $ \del P$ with a probability measure supported on the boundary of $ P'$. In this way, Theorem 1.2 supplies a straightforward strategy to illustrate the caps. In practice, we use polygonal approximations to the planar shape $ P$ with discrete curvature supported on the vertices. See Figs. 10 and 2. A theorem of Reshetnyak states that weak convergence of the curvature distributions as measures on $ \Chat$ implies convergence of the metrics ([Reshetnyak1993], Theorem 7.3.1; [Rešetnjak1960]).
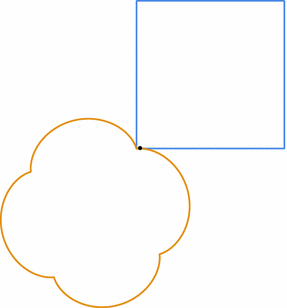
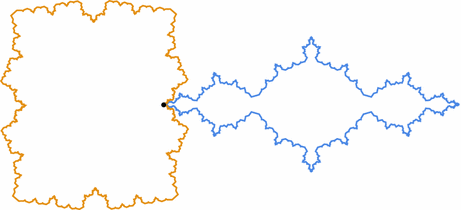
For polygonal planar shapes with arbitrary probability measures $ \mu$ supported on their vertices, our cap-drawing algorithm (which follows the proof of Theorem 1.2) can be used to draw the parametrization $ \hat{s}$, independent of the existence of the metric extension $ \rho(P,\mu)$. For many examples, the curve $ \hat{s}$ fails to form a closed loop or has a shape that cannot be the boundary parametrization of any Euclidean development of a cap (e.g., it may have positive winding number around a point in the plane, while the boundary of a cap development, traversed in the clockwise direction, will wind non-positively around all points). For example, if $ P$ is a triangle, there is a unique measure $ \mu$ supported on the vertices of $ P$ that gives rise to a cap: any associated cap is necessarily a triangle whose sidelengths are the same as those of $ P$, implying the cap is a reflected copy of $ P$, the convex shape is degenerate, and $ \mu(v) = (\pi - \theta)/(2\pi)$ where $ v$ is a vertex of $ P$ with internal angle $ \theta$. In general, the questions of when the metric $ \rho(P,\mu)$ exists and when the cap $ \hat{P}_\mu$ is planar are quite delicate, even in the polygonal setting.
Problem 1.3.
For polygons of $ N$ sides, with side lengths $ \{\ell_1, \ldots, \ell_N\}$ and internal angle $ \theta_i$ at each of its vertices $ v_i$, give an explicit description of the discrete curvature distributions $ \mu = \{\mu_i\}$ supported on the vertices $ v_i$ so that the metric $ \rho(P,\mu)$ exists. Provide conditions under which the polygonal cap $ \hat{P}_\mu$ is planar.Problem 1.3 is related to the geometry of the space of polygons with fixed side lengths and no boundary crossings, which, to our knowledge, has never been described. See [Connelly et al.2003] where it is proved that the space is connected and contractible. The 3-dimensional realization. Recall, by Alexandrov's theorems ([Alexandrov2005], [Aleksandrov1948], [Alexandroff1942, Pogorelov1973]), for nonnegative $ \mu$ there is a unique way to fold the Euclidean development of $ P$ and $ \hat{P}_\mu$ to form the boundary surface of a convex shape in $ \R^3$. We may view the output of the cap-drawing algorithm, as in Figs. 10 and 2, as paper cut-outs to be creased and glued to form the desired shape. Unfortunately, the exact shape of the 3-dimensional realization is not at all clear from the development alone. Even the set of folding lines inside $ P$ and $ \hat{P}_\mu$ is a mystery in general. Quoting from Alexandrov in translation ([Alexandrov2005], p.100), "To determine the structure of a polyhedron from a development, i.e., to indicate its genuine edges in the development, is a problem whose general solution seems hopeless." But in the case of harmonic measure on a planar shape, especially when the shape is the filled Julia set of a polynomial, there may be specialized ways to attack the problem.
Not long ago, Bobenko and Izmestiev devised an illuminating and constructive proof of Alexandrov's realization theorem for polyhedral metrics ([Bobenko and Izmestiev2008]), implementing their algorithm and making it publicly available. Unfortunately, the algorithm was not practical for the polyhedra that closely approximate the metrics for polynomial Julia sets ([Bartholdi2015]). Laurent Bartholdi modified their strategy to handle some dynamical examples, such as the filled Julia set of $ f(z) = z^2-1$ shown in Fig. 3.

Formally, the convex 3D realization of $ (\Chat, \rho(P, \mu))$ determines a Euclidean lamination on the interiors of $ P$ and $ \hat{P}_\mu$, consisting of the geodesic line segments that must be folded to form the 3D shape. We call this the bending lamination of the pair $ (P, \mu)$. If one also retains the data of the dihedral angles (the amount of the fold along each leaf of the lamination), we obtain a measured lamination, uniquely determined by the pair $ (P, \mu)$. We leave the following as an open problem:
Problem 1.4.
Suppose $ \mu$ is the harmonic measure relative to $ \infty$ on the boundary of a planar shape $ P$. Describe the (measured) bending lamination of $ (P,\mu)$.Our research was supported by the National Science Foundation and the Simons Foundation.
2.
Caps, Spirals, and Julia Sets 
In this section, we observe that for every planar shape $ P$,
there is a probability measure $ \mu$ on its boundary so that the
metric $ \rho(P,\mu)$ on $ \Chat$ exists, by simple constructions in
$ \R^2$. We provide examples to illustrate the failure of planarity of a
cap. We conclude the section with examples of harmonic caps coming from
polynomial dynamical systems $ f: \Cak\to \Cak$. Formal definitions and the
proofs of our theorems will be given in Sects. 3 and 4.
Start with a convex polygonal shape in the plane with an external angle
of about $ \pi/16$ at one vertex. Remove two very thin spiral channels
from the polygon that begin on adjacent edges of the polygon and spiral around
one another, as in the left image of Fig. 4. If the spirals are sufficiently intertwined, then
the spiral flaps on the developed naive cap will overlap. The right side of Fig.
4 shows the
spirals reflected across the edges of the polygon.
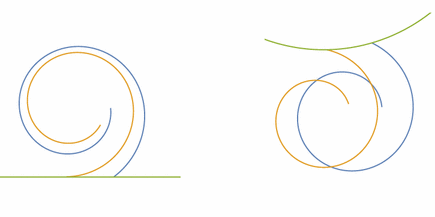
For the harmonic cap, it is possible to construct an example similar
to that of Sect. 2.2. Indeed, very skinny channels removed from
any planar shape will have negligible harmonic measure, and so we can
arrange for overlapping spirals in the cap.
More precisely, begin with a square planar shape and choose a tiny
$ \eps>0$. The harmonic cap for the square is shown in Fig. 10. Now remove
two very skinny spiral channels from the square, emanating from a single edge,
as in the left image of Fig. 5; the openings of each channel should have width
smaller than $ \eps$. The openings of the two spiral channels can be
placed at a specified distance apart from one another, so that the harmonic
measure of the interval between them is approximately equal to $ 1/32$
of the total mass. (The number $ 1/32$ is chosen because it is
$ 1/4\pi$ times the curvature of $ \pi/8$ for the polygon vertex
shown in Fig. 4). We can choose $ \eps>0$ as small we wish
so that the harmonic measure along the spiral boundaries is almost 0. Indeed,
as the width of the spiral channels shrinks to 0, the domains $ \Chat{\setminus} P$ are
converging in the Carath[U+00B4]eodory sense to the complement of the square; see,
e.g., ([Duren1983], [U+00A7]3.1). Recall that the boundary of the cap development is parameterized by
the formula of Theorem 1.2. The parametrization of the spirals on the cap,
which will lie outside the clover-like harmonic cap for the square, will be
essentially equal to a reflection of their original parametrizations (because
$ \kappa$ will be essentially constant along their boundaries, having
chosen the harmonic measure of the spirals to be near 0). On the other hand,
the non-trivial portion of harmonic measure on the boundary of the square
between the spiral-channel openings will curve the boundary of the cap so the
spirals overlap. The change in tangent direction of the clover cap between the
two attaching points of the spirals will be $ \pi/8$, by construction. See
Fig. 5.
Now assume that $ f: \Cak\to\Cak$ is a complex polynomial of degree
$ d\geq 2$. Its filled Julia set
is \begin{eqnarray*} K(f) = \left\{z \in \Cak: \sup_n |f^n(z)| < \infty\right\}. \end{eqnarray*} Assume that $ K(f)$ is connected, so it is a planar shape.
A planar development of its cap is given by the formula of Theorem 1.1. We can
parameterize the boundary of the cap's development for smooth or polygonal
approximations to $ K(f)$ using Theorem 1.2.
The Green function for $ K(f)$ can be computed dynamically,
as \begin{eqnarray*} G_f(z) = \lim_{n\to\infty} \frac{1}{d^n} \log^+|f^n(z)|. \end{eqnarray*} The harmonic measure $ \mu_f = \frac{1}{2\pi} \Delta G_f$ is the unique measure of
maximal entropy for $ f$, and its support is equal to the Julia set
$ J(f) = \del K(f)$ ([Brolin1965, Ljubich1983, Freire et al.1983]). The
metric on $ \Chat$ is defined by \begin{eqnarray*} \rho_f = e^{-2G_f(z)}|dz| \end{eqnarray*} for $ z\in \Cak$, with
curvature distribution $ \omega_f = - \Delta \log \rho_f(z) = 4\pi \mu_f$.
2.1. The Naive Cap.
Let $ P$ be a planar shape that is not contained in a line. Let
$ \bar{P}$ be the convex hull of $ P$ in the plane. The naive cap
$ \hat{P}$ is the union of $ \bar{P}$ and a copy of each connected
component of $ \bar{P} {\setminus} P$ (the flaps
), glued along their boundaries in $ \del \bar{P}$. Then $ P$ and
$ \hat{P}$ glue to determine a degenerate convex body, and the metrized
sphere is a doubled copy of $ \bar{P}$. Its curvature is supported in the
intersection of $ \del P$ with $ \del \bar{P}$. Unfolding the flaps of the
naive cap $ \hat{P}$ determines a Euclidean development. We can appeal
to the Uniformization Theorem or to Reshetnyak's theorem on isothermal
coordinates ([Reshetnyak1993], Theorem 7.1.2) to conclude that
this degenerate surface can be represented as a conformal metric on the
Riemann sphere $ \Chat$.
If $ P$ is an interval, then we can produce a cap by bending
$ P$ into an L-shape in the plane, introducing an angle at the
midpoint of $ P$, and then taking the convex hull of this new shape
in $ \R^2$. Viewing the resulting triangle as a degenerate convex body
in $ \R^3$, we produce a metrized sphere with three concentrated points
of curvature, at the two endpoints of $ P$ and at its midpoint. As
$ P = \del P$ in this example, we have shown the existence of a probability
measure $ \mu$ supported in $ \del P$ and giving rise to a metric
$ \rho(P,\mu)$ on $ \Chat$. The developed cap $ \hat{P}_\mu$ will be a
rhombus. For example, if the angle is chosen to be $ \pi/3$, then the
triangle will be equilateral, and $ \mu$ will assign equal mass to each of
the three cone points.
![]()
2.2. The Naive Cap Is Not
Always Planar.
![]()
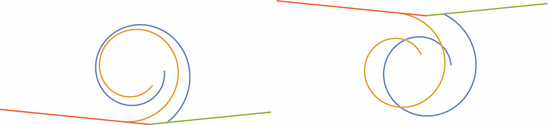
2.3. Non-planar Example for
Harmonic Measure.
![]()
2.4. Polynomial Julia
Sets.
![]()
Example 2.1.
Let $ f(z) = z^2$. Then $ K(f)$ is the
closed unit disk and $ G_f(z) = \log^+|z|$. The measure $ \mu_f$ is the
Lebesgue measure on the circle. By symmetry, the harmonic cap is also a
closed disk of radius 1. It follows that the convex realization in $ \R^3$
is a degenerate closed disk. Example 2.2.
Let $ f(z)= z^2-2$. Then $ K(f)$ is the
real interval $ [-2,2]$, and the metric on the sphere and the Euclidean
development of the harmonic cap can be computed explicitly. The Riemann
map from the complement of the unit disk to the complement of $ K(f)$
is given by \begin{eqnarray*} \Phi_f(z) = z+ \frac{1}{z}. \end{eqnarray*} Applying Theorem 1.1, the cap is
the image of the holomorphic function $ g: \D\to \Cak$ defined by \begin{eqnarray*} g(z) = \int_0^z \Phi_f'(1/x) \, dx = \int_0^z (1 - z^2) \, dz = z - z^3/3. \end{eqnarray*}
See Fig. 6. The convex realization in $ \R^3$ is
degenerate. 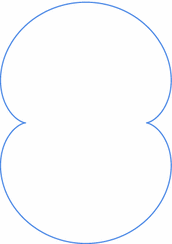
Example 2.3.
Let $ f(z) = z^2 + 1/4$. A polygonal
approximation to its filled Julia set and the harmonic cap are shown in Fig.
7.
The convex realization in $ \R^3$ is nondegenerate; indeed, if the filled
Julia set were contained in a plane in $ \R^3$, then its convex hull
would also lie in the surface, and then the curvature could not be supported
on all of $ J(f)$. 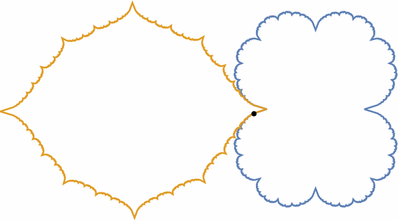
3. Metrics and Curvature

In this section, we formalize the notions of curvature and metric from
the point of view of Euclidean geometry, and we prove Theorem 1.2. In
Proposition 3.1, we present an asymptotic formula for
curvature when the boundary of the planar shape is a smooth Jordan curve, in
terms of the circumference of small circles.
A convex polyhedron in $ \R^3$ is the intersection of finitely
many closed halfspaces. It is said to be degenerate if it lies in a plane. When the
polyhedron is non-degenerate and bounded, its boundary surface is topologically
a sphere, and the Euclidean metric from $ \R^3$ induces an intrinsic
path metric on the sphere. If the polyhedron is degenerate and bounded, but
not contained in a line, we will still view its boundary as a topological sphere,
doubling the planar polygon and gluing along the polygonal boundary. Abstractly, a convex polyhedral metric on a 2-dimensional sphere is
an intrinsic metric with non-negative curvature concentrated at finitely many
points. In other words, in a small neighborhood of all but finitely many points,
the surface is isometric to a region in $ \R^2$. In a neighborhood of
each of the finitely many cone points
, the surface is isometric to the point of a cone. The curvature
of a cone point is equal to the angle deficit at the point; that is, if the
circumference of any small circle of radius $ r$ centered at the cone
point is equal to $ C(r)$, then the curvature is equal to $ (2\pi r - C(r))/r$.
By the Gauss-Bonnet formula, the sum of the curvatures over all cone points
on the sphere is equal to $ 4\pi$.
[Alexandrov2005] examines the geometry of convex
polyhedra in detail. He presents his proof from [Alexandroff1942] that
any abstract polyhedral metric on a sphere is isometric to the boundary of a
(possibly degenerate) convex polyhedron.
Furthermore, the polyhedron in $ \R^3$ is unique, up to Euclidean
isometries.
Given a polyhedral metric on the sphere, and a simply-connected subset
$ U$ of the sphere minus its cone points, a Euclidean development
of $ U$ is a local isometry $ U \to \R^2$. Suppose we are given the
image $ \mathcal{I}\subset \R^2$ of a Euclidean development of a full-area,
simply-connected subset $ U$ of the sphere. Then, as a consequence
of Alexandrov's theorem, the convex polyhedron in $ \R^3$ is uniquely
determined by $ \mathcal{I}$ and the gluing along its boundary (that
reconstructs the topological sphere). In particular, the planar development
and the gluing information will uniquely determine the edges of the
polyhedron and their dihedral angles in $ \R^3$---information that is
not locally apparent.
Curvature is carefully treated by Alexandrov. It is defined by an
additive set function $ \omega$ as follows. The curvature of a point is, as
for a polyhedron, $ 2\pi$ minus the cone angle of the point. That is,
Reshetnyak, who was a student of Alexandrov, reformulated
Alexandrov's theory of metrics and curvature on a surface in complex-analytic
language, expressing curvature as a finite Borel measure ([Reshetnyak1993]). We exploit this useful point of
view in Sect. 4.
Suppose that a planar shape $ P$ is the closure of a Jordan
domain with a piecewise-differentiable boundary. Fix a nonnegative Borel
measure $ \mu$ on the boundary of $ P$. Let $ L$
be the length of $ \del P$. Let $ s$ be a piecewise-differentiable
parametrization by arclength of the boundary of $ P$, in the
counterclockwise direction, and write \begin{eqnarray*} s'(t) = e^{i \alpha(t)} \end{eqnarray*} for a piecewise-continuous
function $ \alpha: [0,L] \to \R$. For $ t \in [0, L]$, we define a curvature function
$ \kappa: [0,L] \to [0, 4\pi]$ by $ \kappa(0) = 0$ and If $ \hat{P}_\mu$ exists, then it has a polygonal boundary with the
same edge lengths as $ P$. We label its vertices in the clockwise
direction by $ \hat{v}_0, \hat{v}_1, \ldots, \hat{v}_N = \hat{v}_0$. We may assume for simplicity that $ \hat{v}_0 = v_0$
and $ \hat{v}_1 = v_1$. The curvature condition implies that the internal angle
$ \hat{\theta}_j$ at vertex $ \hat{v}_j$ must satisfy \begin{eqnarray*} 4\pi \mu(v_j) = 2\pi - \theta_j - \hat{\theta}_j. \end{eqnarray*} Therefore, the
clockwise parametrization $ \hat{s}$ of $ \hat{P}_\mu$ will satisfy
$ \hat{s}'(t) = e^{i \hat{\alpha}(t)}$ with \begin{eqnarray*} \hat{\alpha}(t) &=& - \sum_{j=1}^{k-1} (\pi - \hat{\theta}_j) \quad \mbox{for } \sum_{j=1}^{k-1} \ell_j \leq t < \sum_{j=1}^k \ell_j \\ &=& \alpha(t) - \sum_{j=1}^{k-1} 4\pi \mu(v_j) \quad \mbox{for } \sum_{j=1}^{k-1} \ell_j \leq t < \sum_{j=1}^k \ell_j \\ &=& \alpha(t) - \kappa(t) \end{eqnarray*} In other words, the parametrization of the
boundary of $ \hat{P}_\mu$ is given in a clockwise orientation by \begin{eqnarray*} \hat{s}(t) = \int_0^t e^{i (\alpha(x) - \kappa(x))} \, dx. \end{eqnarray*}
If $ P$ is an arbitrary planar shape with
piecewise-differentiable boundary, and if $ \mu$ is any probability
measure supported on the boundary of $ P$, then the pair
$ (P, \mu)$ can be approximated by a sequence of polygons $ (P_n, \mu_n)$
so that the vertices of $ P_n$ lie in $ \del P$ for all $ n$,
and $ \mu_n$ is a discrete probability measure supported on the vertices
of $ P_n$. We may construct the polygons $ P_n$ so that the
arclength parametrizations $ s_n$ of $ \del P_n$ converge uniformly
to $ s$ and that the angle functions $ \rho_n \to \rho$ uniformly.
Furthermore, by choosing the vertices of $ P_n$ carefully, we may
assume that for every $ \eps>0$, all atoms of mass at least $ \eps$
for $ \mu$ are vertices of $ P_n$ and atoms of $ \mu_n$ for
all $ n\geq n(\eps) > 0$. In this way, we can also arrange that the curvature
functions $ \kappa_n$ converge uniformly to the curvature function
$ \kappa$. These choices for $ (P_n, \mu_n)$ imply that the integrals
\begin{eqnarray*} \int_0^t e^{i (\rho_n(x) - \kappa_n(x))} \, dx \longrightarrow \int_0^t e^{i (\rho(x) - \kappa(x))} \, dx \end{eqnarray*} as $ n\to \infty$ for all $ t \in [0, |\del P|]$. In other words, if the cap
$ \hat{P}_\mu$ exists
, then the desired boundary parametrization will be uniformly approximated
by the curves $ \hat{s}_n$ defined by \begin{eqnarray*} \hat{s}_n(t) = \int_0^t e^{i (\rho_n(x) - \kappa_n(x))} \, dx. \end{eqnarray*} Note that the curves
$ \hat{s}_n$ are not necessarily closed loops, as the approximating polygonal
caps $ \hat{P}_{\mu_n}$ may not exist. $ \square$ ⬜
If the boundary of the planar domain $ P$ and the measure
$ \mu$ are smooth enough, then the curvature of Sect. 3.2
satisfies the following relation, as a consequence of Theorem 1.2.
It is interesting to compare the statement of Proposition 3.1 to the
formula (3.1) for the Alexandrov curvature of a point,
\begin{eqnarray*} \omega(\{x\}) = \lim_{r\to 0^+} \frac{2\pi r - C(x,r)}{r}, \end{eqnarray*} and to the Bertrand--Puiseux formula for the Gaussian curvature
$ \kappa$ when the metric on a surface is smooth, \begin{eqnarray*} \kappa(x) = \; \lim_{r\to 0^+} \; 3 \, \frac{2\pi r - C(x,r)}{\pi r^3} \end{eqnarray*} ([Spivak1979], page 147). In our setting, the
curvature of the surface is supported on a 1-dimensional curve, so the
circumference discrepancy is proportional to $ r^2$. We begin with a simple geometric lemma. The curvature function of Eq. (3.2) is
computed as \begin{eqnarray*} \kappa(t) = \mu(s(0,t]) = \int_0^t \delta(x) \,dx. \end{eqnarray*} For each $ t\in [0,L]$ and each small
$ r>0$, the circumference $ C(s(t),r)$ is the sum of the lengths of
two circular arcs: the arc in $ P$ to the "left" of $ s(t)$
(relative to the counterclockwise orientation on $ \partial P$), whose length
we will denote by $ C_r(t)$, and the arc in $ \hat{P}_\mu$ to the "right" of
$ \hat{s}(t)$ (relative to the clockwise orientation on $ \partial \hat{P}_\mu$), whose
length we will denote by $ \hat{C}_r(t)$. Classical plane geometry tells us that
the radius of the osculating circle to the plane curve $ s$ at
$ s(t)$ is $ 1/| s^{\prime \prime}(t) | = 1/|\alpha^{\prime}(t)|$, using the notation of Theorem 1.2.
Likewise, from Theorem 1.2, the radius of the osculating circle to the plane
curve $ \hat{s}$ at $ \hat{s}(t)$ equals $ 1/ | \hat{s}^{\prime \prime}(t)| = 1/ | \alpha^{\prime}(t) - \kappa^{\prime}(t)|$. For $ \alpha^{\prime}(t) > 0$, the osculating circle is to the left of $ s(t)$,
so \begin{eqnarray*} \lim_{r \rightarrow 0} \frac{\pi r - C_r(t)}{r^2} = |\alpha^{\prime}(t)| = \alpha^{\prime}(t) \end{eqnarray*} by Lemma 3.2. For $ \alpha^{\prime}(t) < 0$, the osculating circle is to
the right of $ s(t)$, so \begin{eqnarray*} \lim_{ r\rightarrow 0} \frac{\pi r - C_r(t)}{r^2} = \lim_{r \rightarrow 0} \frac{ \pi r - \left(2\pi r - A\left(\frac{1}{|\alpha^{\prime}(t)|},r\right)\right)}{r^2} = - | \alpha^{\prime}(t)| = \alpha^{\prime}(t) \end{eqnarray*} by Lemma 3.2. Thus
$ \lim_{r \rightarrow 0} \frac{ \pi r - C_r(t)}{r^2} = \alpha^{\prime}(t)$, regardless of the sign of $ \alpha'(t)$. Similarly, \begin{eqnarray*} \lim_{r \rightarrow 0} \frac{ \pi r - \hat{C}_r(t)}{r^2} = -(\alpha^{\prime}(t) - \kappa'(t)) = \delta(t) - \alpha^{\prime}(t) \end{eqnarray*}
regardless of the sign of $ \alpha^{\prime}(t) - \kappa'(t)$. Hence, \begin{eqnarray*} \lim_{r \rightarrow 0} \frac{2\pi r - C(s(t),r)}{r^2}& =& \lim_{r \rightarrow 0} \frac{ \pi r - C_r(t)}{r^2} + \lim_{r \rightarrow 0} \frac{ \pi r - \hat{C}_r(t)}{r^2}\\ & =& \alpha^{\prime}(t) + \delta(t) - \alpha^{\prime}(t) =\delta(t). \end{eqnarray*} $ \square$
⬜
3.1. Polyhedra and Cone Angles
![]()
3.2. More General Metrics of
Non-negative Curvature.
[Aleksandrov1948] presents the proof of a more
general realization result; see Chapter 1 of [Pogorelov1973] for a summary. Given any abstract intrinsic metric on the sphere of
non-negative curvature, it is realizable as the boundary of a (possibly
degenerate) convex body in
$ \R^3$. His argument relies on a convergence statement, first
approximating the metric by polyhedral metrics, realizing the convex
polyhedra, and then showing that the polyhedra converge to the desired
convex body in $ \R^3$.
![]()
\begin{eqnarray}\label{pointcurvature} \omega(\{x\}) = \lim_{r\to 0^+} \frac{2\pi r - C(x,r)}{r} \end{eqnarray}
(3.1)
3.3. Parametrization of the Cap
![]()
\begin{eqnarray} \label{curvaturefunction} \kappa(t) = 4\pi \mu(s(0,t]) \end{eqnarray}
(3.2)
Proof of Theorem
1.2.
Suppose first that $ P$ is a polygon in
the complex plane and $ \mu$ is a discrete probability measure
supported on the vertices of $ P$. Denote the vertices of
$ P$ by $ v_0, v_1, \ldots, v_N = v_0$, oriented counterclockwise, and set
\begin{eqnarray*} \ell_j = |v_j - v_{j-1}| \end{eqnarray*} to be the length of the $ j$-th edge. We may assume for
simplicity that $ v_0 = 0$ and $ v_1 = \ell_1$ lies on the positive real axis.
Let $ \theta_j$ be the internal angle of $ P$ at vertex
$ v_j$, so that \begin{eqnarray*} \sum_{j=1}^N (\pi - \theta_j) = 2\pi \end{eqnarray*} and \begin{eqnarray*} \alpha(t) = \sum_{j=1}^{k-1} (\pi - \theta_j) \quad \mbox{for}\quad \sum_{j=1}^{k-1} \ell_j \leq t < \sum_{j=1}^k \ell_j \end{eqnarray*} for each $ k = 1, \ldots N$.
Thus $ P$ is parameterized by \begin{eqnarray*} s(t) = \int_0^t e^{i\alpha(x)} \, dx. \end{eqnarray*}
3.4. Circumference and
Curvature.
![]()
Proposition 3.1.
Let $ P$ be a planar shape with
boundary parametrized by arclength by $ s: [0,L] \to \del P$ such that $ s$
is twice continuously-differentiable, and let $ \mu$ be a probability
measure on $ \del P$ which is absolutely continuous with respect to
arclength with a continuous density function. Suppose the metric
$ \rho(P,\mu)$ exists. For each $ x \in \del P$, let $ C(x,r)$ denote the
circumference of a circle in $ (\Chat, \rho(P,\mu))$ centered at $ x$ of radius
$ r>0$. Then \begin{eqnarray*} \lim_{r\to 0^+} \frac{2\pi r - C(s(t),r)}{r^2} = \delta(t), \end{eqnarray*} where $ s^*\mu = \delta(t)\,dt$ on the interval
$ [0,L]$. Lemma 3.2.
For real numbers $ R>r>0$, let
$ A(R,r)$ be the arclength of the intersection of a closed disk of radius
$ R$ and a circle of radius $ r$ centered at a boundary
point of the disk. Then \begin{eqnarray*} \lim_{r \rightarrow 0^+} \frac{\pi r - A(R,r)}{r^2} = \frac{1}{R}. \end{eqnarray*}
Proof.
Assume the center of the radius $ r$ circle is at the origin in
$ \mathbb{R}^2$, and the disk of radius $ R$ is tangent to the x-axis at
the origin. These two circles are given by the equations $ x^2+(y-R)^2 = R^2$ and
$ x^2+y^2=r^2.$ These two circles intersect in two points: $ ( \pm \sqrt{r^2-\frac{r^4}{4R^2}},\frac{r^2}{2R} )$. Hence,
$ A(R,r) = r (\pi - 2 \tan^{-1} (\frac{r^2}{\sqrt{4R^2r^2-r^4}})).$ Then \begin{eqnarray*} \lim_{r \rightarrow 0^+} \frac{\pi r - A(R,r)}{r^2} = \lim_{r \rightarrow 0^+} \frac{ 2 \tan^{-1}\left(\frac{r^2}{\sqrt{4R^2r^2-r^4}}\right)}{r}= \frac{1}{R}. \end{eqnarray*} $ \square$ ⬜
Proof of
Proposition 3.1.
4. Harmonic Measure and Holomorphic
1-Forms

In this section, we present curvature in the setting of conformal
metrics, allowing us to use tools from complex analysis to address our
geometric questions. This perspective was first formalized by [Reshetnyak1993]. We present the proof of Theorem
1.1 and
derive an alternative proof of the parametrization of the harmonic cap from
Theorem 1.2. Finally, we revisit the general problem of
existence of the metric $ \rho(P,\mu)$ in Proposition 4.2.
A smooth conformal metric on a domain in $ \Cak$ can be
expressed as \begin{eqnarray*} \rho(z) |dz| \end{eqnarray*} for a smooth and positive function $ \rho$.
The metric has non-negative curvature if $ U(z) = -\log \rho(z)$ is a subharmonic
function. Working with a more general class of metrics, we will only require
that $ U$ be subharmonic, not necessarily differentiable or
everywhere finite. We will also require that all pairs of points have finite
distance from one another. These requirements can be formulated in terms of
the curvature of the metric, as we explain below. Formally, a conformal metric $ \rho$ on $ \Chat$ is a
(singular) Hermitian metric on the tangent bundle $ T\Chat \simeq \mathcal{O}_{\P^1}(2)$, and the
curvature form of the metric is the positive measure given in local coordinates
by \begin{eqnarray*} \omega_\rho = - \Delta \log \rho \end{eqnarray*} (with $ \Delta = 2i \del \delbar$ taken in the sense of distributions), so
that \begin{eqnarray*} \int_{\Chat} \omega_\rho = 4\pi. \end{eqnarray*} In more classical terms, for a smooth metric $ \rho$,
the Gaussian curvature is computed locally as \begin{eqnarray*} \kappa_\rho = \frac{-\Delta \log \rho}{\rho^2}. \end{eqnarray*} See, for example,
([Ahlfors1973], [U+00A7]1.5) or ([Hubbard2006], [U+00A7]2.2). That $ U = -\log\rho$ is subharmonic guarantees that the curvature
form $ \omega_\rho \geq 0$ as a distribution. Finite diameter is guaranteed by the
assumption that $ \omega_\rho(\{z_0\}) < 2\pi$ for all $ z_0 \in \Chat$ ([Reshetnyak1993], p. 100). Recall from Sect. 3.4 that concentrated curvature, at points
$ z_0 \in\Chat$ where $ 0 < \omega_{\rho}(\{z_0\}) < 2\pi$, corresponds to cone points in the local
geometry. Also in this setting, a computation shows that the circumference
$ C(z_0, r)$ of a small circle around $ z_0$ of radius $ r>0$
will satisfy ([Reshetnyak1993], Lemma 8.1.1) \begin{eqnarray*} \lim_{r \to 0^+} \frac{2\pi r - C(z_0,r)}{r} = \omega_{\rho}(\{z_0\}). \end{eqnarray*} Conversely, every probability measure $ \mu$ on
$ \Chat$ with $ \mu(\{z\}) < 1/2$ for all $ z$ gives rise to a
conformal metric of finite diameter with curvature distribution $ 4\pi \mu$,
unique up to scale. Indeed, there is a one-to-one correspondence between
probability measures $ \mu$ on $ \Chat$ and their potentials, up
to an additive constant, which can be viewed as logarithmically-homogeneous,
plurisubharmonic functions $ G_\mu$ on the tautological line bundle
$ \Cak^2{\setminus} \{(0,0)\} \to \P^1$; see, e.g., ([Forn[U+00E6]ss and Sibony1993], Theorem 5.9) and
([DeMarco2003], Section 12). The function
$ G_\mu$ will satisfy $ (2\pi)^{-1} \Delta G_\mu(z,1) = \mu$ in local coordinates $ z$ on
$ \Chat$, and the conformal metric is expressed as \begin{eqnarray*} \rho_\mu = e^{-2 G_\mu(z,1)} |dz|. \end{eqnarray*} The
identification between measures and their potentials is continuous, taking the
$ L^1_{loc}$ topology on potentials and the weak topology on measures.
Moreover, convergence of curvatures implies convergence of the metrics
([Reshetnyak1993], Theorem 7.3.1).
Let $ P$ be a compact, connected set in $ \Cak$
containing at least 2 points, so that $ P$ is a planar shape as defined
in Sect. 1.
Let $ G_P: \Cak\to \R$ be the Green function for $ P$; it is the unique
continuous function on $ \Cak$ satisfying (1) $ G_P \equiv 0$ on
$ P$, (2) $ G_P(z) = \log|z| + O(1)$ for $ z$ near $ \infty$, and
(3) $ G_P$ is harmonic on $ \Cak{\setminus} P$. Then define a metric on
$ \Cak$ by \begin{eqnarray*} \rho_P = e^{-2G_P(z)} |dz|. \end{eqnarray*} By elementary potential theory, the function
$ G_P$ satisfies $ G_P(z) = \log(z) + \gamma + o(1)$ for $ z$ near $ \infty$ for
some real number $ \gamma$, so the metric extends uniquely by continuity
across $ z=\infty$. Note that this metric is flat
(with 0 curvature) away from the boundary $ \del P$. Its curvature form
$ \omega_P = 2 \Delta G_P$ is equal to ($ 4\pi$ times) the harmonic measure on
$ \del P$ (more precisely, the harmonic measure for the domain
$ \Chat{\setminus} P$, relative to the point $ \infty$). Let $ P$ be any planar shape. Let $ \Phi$ be the
Riemann map from the complement of the unit disk to the complement of
$ P$, sending infinity to infinity. Consider the holomorphic 1-form
\begin{eqnarray*} \eta = \frac{1}{(\Phi^{-1}(z))^2} \; dz \end{eqnarray*} on the complement of $ P$. Since the Green function
satisfies \begin{eqnarray*} G_P(z) = \log|\Phi^{-1}(z)| \end{eqnarray*} on $ \Chat{\setminus} P$, we see that $ |\eta|$ is precisely
the conformal metric $ \rho_P$ defined above, when restricted to the
complement of $ P$. Recall that Theorem 1.1 asserts that
a Euclidean development of the harmonic cap of $ P$ is given by the
locally univalent function $ g: \D\to\Cak$ defined by \begin{eqnarray*} g(z) = \int_0^z \Phi'(1/x) \, dx. \end{eqnarray*} It also asserts
that there exist examples where the locally univalent $ g$ fails to be
univalent.
It remains to observe that there exist planar shapes $ P$ for
which the development $ g$ fails to be injective. We constructed
such an example in Sect. 2.3, where $ P$ is a square minus two
thin spiral channels. $ \square$ ⬜
Here we present an alternative proof of the cap parametrization in
Theorem 1.2, in the special setting of harmonic measure.
As in Theorem 1.2, assume that $ P$ has a
piecewise-differentiable boundary which is a Jordan curve parameterized by
arclength by $ s: [0,L] \to \Cak$. Recall that $ s^{\prime}(t) = e^{i \alpha(t)}$ for some piecewise
continuous function $ \alpha:[0,L] \rightarrow \R$. Let $ \Phi$ be a Riemann map from
the complement of the unit disk to the complement of $ P$, sending
infinity to infinity. Then $ \Phi$ extends to a homeomorphism from the
unit circle to the boundary of $ P$. Define the conformal angle
$ \theta: [0,L] \rightarrow \R$ by \begin{eqnarray*} \theta(t) := \mathrm{arg}(\Phi^{-1}(s(t))). \end{eqnarray*} Without loss of generality, we may assume
$ \theta(0)=0$ so that $ \theta$ defines a homeomorphism from
$ [0,L]$ to $ [0,2\pi]$. It follows that the curvature function of
(3.2) for the harmonic measure $ \mu$ on
$ \del P$ is equal to \begin{eqnarray*} \kappa(t) = 4\pi \mu(s(0,t]) = 2\theta(t). \end{eqnarray*} Therefore, from Theorem 1.2, we
know that the parametrization of the boundary of the harmonic cap is given
by Theorem 1.1 grants an alternate proof of (4.1). Indeed,
with the $ g: \D \to \Cak$ of Theorem 1.1, a parametrization of the boundary of the
harmonic cap is given by \begin{eqnarray*} \hat{s}(t) = -g(1/\Phi^{-1}(s(t))) = -g(e^{-i\theta(t)}). \end{eqnarray*} Moreover, the derivative of
$ g$ is $ g'(z) = \Phi'(1/z)$, and therefore, \begin{eqnarray*} \hat{s}'(t) &=& -g'(1/\Phi^{-1}(s(t)))\frac{-(\Phi^{-1})'(s(t)) \; s'(t)}{\Phi^{-1}(s(t))^2} \\ &=& \frac{-\Phi'(\Phi^{-1}(s(t)))}{-\Phi'(\Phi^{-1}(s(t)))} \; \frac{s'(t)}{\Phi^{-1}(s(t))^2} \\ &=& e^{i(\alpha(t) - 2\theta(t))}. \end{eqnarray*}
We conclude by returning to our original problem about the existence of
a metric $ \rho(P,\mu)$, for the case where $ P$ is a planar shape with
Jordan curve boundary and the probability measure $ \mu$ is arbitrary.
Suppose that $ J$ is a Jordan curve in $ \Chat$,
cutting the sphere into Jordan domains $ A$ and $ B$. We
may assume that $ 0 \in A$ and $ \infty \in B$. Suppose that
$ \nu$ is a probability measure supported on $ J$, and let
\begin{eqnarray*} U(z) = \int_\Cak \log|z-w| \, d\nu(w) \end{eqnarray*} be a potential function for $ \nu$ with logarithmic
singularity at $ \infty$. The conformal metric \begin{eqnarray*} e^{-2U(z)}|dz| \end{eqnarray*} on
$ \Cak$ extends to $ \Chat$ and has curvature distribution equal
to $ 4\pi\nu$. Since $ A$ is simply connected, there exists a
non-vanishing analytic function $ \phi: A \to \Cak$ so that \begin{eqnarray*} U(z) = \log|\phi(z)|. \end{eqnarray*} The
function $ \phi$ is determined uniquely, up to postcomposition by a
rotation. Set \begin{eqnarray*} f_\nu(z) = \int_0^z \frac{dz}{\phi(z)^2} \end{eqnarray*} for $ z \in A$. Then $ f_\nu: A \to \Cak$ is a
locally-univalent Euclidean development of $ A$ into the plane. It
extends continuously to the boundary curve $ J$. This proves the
following proposition. When $ \mu$ is the harmonic measure on $ \del P$,
observe that we may take $ J = \del P$ and $ \nu = \mu$ in the statement of
Proposition 4.2. Indeed, the potential function for harmonic
measure satisfies $ U \equiv 0$ on $ P$ so that $ f_\nu = \mathrm{Id}$.
4.1. Complex-Analytic Point of View
![]()
4.2. Harmonic Measure as
Curvature.
![]()
Example 4.1.
Let $ P$ be the closed unit disk.
Then $ G_P(z) = \log^+|z| = \max\{0, \log|z|\}$, and the curvature form $ \omega_P$ is arclength
measure on the unit circle, normalized to have total length $ 4\pi$. By
the symmetry of $ P$, it is not hard to see that Alexandrov's
realization of $ (\Chat, \rho_P)$ will be the degenerate doubled flat disk.
4.3. The Harmonic Cap
![]()
Proof of Theorem
1.1.
Define $ F: \Chat{\setminus} P \to \Cak$ by \begin{eqnarray*} F(z) = \int_\infty^z \eta \; = \int_\infty^z \frac{1}{(\Phi^{-1}(\zeta))^2} \, d\zeta. \end{eqnarray*} By
definition, we have $ \eta = dF = F^* (dw)$, where $ dw$ is the standard
holomorphic 1-form on the plane. Since $ |\eta|$ is the desired conformal
metric, and since $ |\eta| = F^* |dw|$, we conclude that $ F$ is a
Euclidean development of the harmonic cap parametrized by $ z$ in
$ \Chat{\setminus} P$. Now set $ \iota(x) = 1/x$. Then, to parameterize the cap by
$ z \in \D$, we pull $ \eta$ back to $ \D$ by $ \Phi\circ \iota$,
so that \begin{eqnarray*} D(z) = \int_0^z \iota^* \Phi^* \eta = \int_0^z \iota^* \left( \frac{\Phi'(\zeta)}{\zeta^2} \, d\zeta \right) = - \int_0^z \Phi'(1/x) \, dx. \end{eqnarray*} The local invertibility of $ D$ is clear because
$ D'(z) = - \Phi'(1/x) \not= 0$ for all $ x \in \D$. Our desired function is $ g(z) = -D(z)$,
which is clearly an isometric presentation.
4.4. Harmonic Cap Boundary
Parametrization
![]()
\begin{eqnarray} \label{shattheta} \hat{s}(t) = \int_0^t e^{i(\alpha(x) - 2\theta(x))} \, dx. \end{eqnarray}
(4.1)
4.5. Metric Existence for General
Measures
![]()
Proposition 4.2.
Let $ P$ be a planar shape with
Jordan curve boundary, and let $ \mu$ be a probability measure
supported on $ \del P$. The metric $ \rho(P,\mu)$ on $ \Chat$ exists
if and only if there is a pair $ (J, \nu)$ of a Jordan curve bounding a region
$ A$ in $ \Chat$ and probability measure supported on
$ J$ so that $ f_\nu(A) = P$ and $ (f_\nu)_*\nu = \mu$.
References
[Aleksandrov1948] Aleksandrov, A.D.: Vnutrennyaya Geometriya Vypuklyh Poverhnoste[U+02D8][U+0131]. OGIZ, Moscow (1948)
[Alexandroff1942] Alexandroff, A.: Existence of a convex polyhedron and of a convex surface with a given metric. Rec. Math. [Mat. Sbornik] N.S. 11 (53), 15--65 (1942)
[Alexandrov2005] Alexandrov, A.D.: Convex polyhedra. Springer Monographs in Mathematics. Springer, Berlin (2005) (translated from the 1950 Russian edition by N. S. Dairbekov, S. S. Kutateladze and A. B. Sossinsky, with comments and bibliography by V. A. Zalgaller and appendices by L. A. Shor and Yu. A. Volkov)
[Bartholdi2015] Bartholdi, L.: Personal communication (2015)
[Bobenko and Izmestiev2008] Bobenko, A.I., Izmestiev, I.: Alexandrov's theorem, weighted Delaunay triangulations, and mixed volumes. Ann. Inst. Fourier (Grenoble) 58 (2), 447--505 (2008)
[Brolin1965] Brolin, H.: Invariant sets under iteration of rational functions. Ark. Mat. 6 (103--144), 1965 (1965)
[Connelly et al.2003] Connelly, R., Demaine, E.D., Rote, G.: Straightening polygonal arcs and convexifying polygonal cycles. Discrete Comput. Geom. 30 (2), 205--239 (2003) [U.S.-Hungarian Workshops on Discrete Geometry and Convexity (Budapest, 1999/Auburn, AL, 2000)]
[Demaine and O'Rourke2005] Demaine, E.D., O'Rourke, J.: A survey of folding and unfolding in computational geometry. In: Combinatorial and Computational Geometry, Math. Sci. Res. Inst. Publ., vol. 52, pp. 167--211. Cambridge Univ. Press, Cambridge (2005)
[Demaine and O'Rourke2007] Demaine, E.D., O'Rourke, J.: Geometric Folding Algorithms. Cambridge University Press, Cambridge (2007) (Linkages, origami, polyhedra)
[DeMarco2003] DeMarco, L.: Dynamics of rational maps: Lyapunov exponents, bifurcations, and capacity. Math. Ann. 326 (1), 43--73 (2003)
[Duren1983] Duren, P.L.: Univalent functions. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 259. Springer, New York (1983)
[Forn[U+00E6]ss and Sibony1993] Forn[U+00E6]ss, J.E., Sibony, N.: Complex dynamics in higher dimensions. In: Complex Potential Theory (Montreal, PQ, 1993), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 439, pp. 131--186. Kluwer Acad. Publ., Dordrecht (1994) (Notes partially written by Estela A. Gavosto)
[Freire et al.1983] Freire, A., Lopes, A., Ma~né, R.: An invariant measure for rational maps. Bol. Soc. Brasil. Mat. 14 (1), 45--62 (1983)
[Hubbard and Papadopol1994] Hubbard, J., Papadopol, P.: Superattractive fixed points in $ { c}^n$. Indiana Univ. Math. J. 43 , 321--365 (1994)
[Hubbard2006] Hubbard, J.H.: Teichm[U+00A8]uller theory and applications to geometry, topology, and dynamics, vol. 1. Matrix Editions, Ithaca (2006). Teichm[U+00A8]uller theory, with contributions by Adrien Douady, William Dunbar, Roland Roeder, Sylvain Bonnot, David Brown, Allen Hatcher, Chris Hruska and Sudeb Mitra, with forewords by William Thurston and Clifford Earle
[Ljubich1983] Ju, M.: Ljubich. Entropy properties of rational endomorphisms of the Riemann sphere. Ergodic Theory Dyn. Syst. 3 (3), 351--385 (1983)
[Pogorelov1973] Pogorelov, A.V.: Extrinsic Geometry of Convex Surfaces. American Mathematical Society, Providence (1973) (translated from the Russian by Israel Program for Scientific Translations, Translations of Mathematical Monographs, vol. 35)
[Pommerenke1992] Pommerenke, Ch.: Boundary Behaviour of Conformal Maps. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 299. Springer, Berlin (1992)
[Rešetnjak1960] Rešetnjak, Ju.G.: Isothermal coordinates on manifolds of bounded curvature. I, II. Sibirsk. Mat. [U+02C7]Z. 1 , 88--116, 248--276 (1960)
[Reshetnyak1993] Reshetnyak, Yu.G.: Two-dimensional manifolds of bounded curvature. In: Geometry, IV, Encyclopedia Math. Sci., vol. 70 , pp. 3--163, 245--250. Springer, Berlin (1993)
[Series2006] Series, C.: Thurston's bending measure conjecture for once punctured torus groups. In: Spaces of Kleinian Groups, London Math. Soc. Lecture Note Ser., vol. 329, pp. 75--89. Cambridge Univ. Press, Cambridge (2006)
[Spivak1979] Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol. II, 2nd edn. Publish or Perish Inc, Wilmington (1979)
[Thurston1998] Thurston, W.P.: Shapes of polyhedra and triangulations of the sphere. In: The Epstein Birthday Schrift, Geom. Topol. Monogr., vol. 1, pp. 511--549. Geom. Topol. Publ., Coventry (1998)
[The Sage Developers2016] The Sage Developers. Sage Mathematics Software (Version 6.10.beta7) (2016).
[Van Andel and Bradshaw2011] Van Andel, E., Bradshaw, R.: Riemann mapping [sage mathematics software package] (2011)
- 99
- × Ahlfors, L.V.: Conformal Invariants: Topics in Geometric Function Theory, McGraw-Hill Series in Higher Mathematics. McGraw-Hill Book Co., New York (1973)
- × Aleksandrov, A.D.: Vnutrennyaya Geometriya Vypuklyh Poverhnoste[U+02D8][U+0131]. OGIZ, Moscow (1948)
- × Alexandroff, A.: Existence of a convex polyhedron and of a convex surface with a given metric. Rec. Math. [Mat. Sbornik] N.S. 11 (53), 15--65 (1942)
- × Alexandrov, A.D.: Convex polyhedra. Springer Monographs in Mathematics. Springer, Berlin (2005) (translated from the 1950 Russian edition by N. S. Dairbekov, S. S. Kutateladze and A. B. Sossinsky, with comments and bibliography by V. A. Zalgaller and appendices by L. A. Shor and Yu. A. Volkov)
- × Bartholdi, L.: Personal communication (2015)
- × Bobenko, A.I., Izmestiev, I.: Alexandrov's theorem, weighted Delaunay triangulations, and mixed volumes. Ann. Inst. Fourier (Grenoble) 58 (2), 447--505 (2008)
- × Brolin, H.: Invariant sets under iteration of rational functions. Ark. Mat. 6 (103--144), 1965 (1965)
- × Connelly, R., Demaine, E.D., Rote, G.: Straightening polygonal arcs and convexifying polygonal cycles. Discrete Comput. Geom. 30 (2), 205--239 (2003) [U.S.-Hungarian Workshops on Discrete Geometry and Convexity (Budapest, 1999/Auburn, AL, 2000)]
- × Demaine, E.D., O'Rourke, J.: A survey of folding and unfolding in computational geometry. In: Combinatorial and Computational Geometry, Math. Sci. Res. Inst. Publ., vol. 52, pp. 167--211. Cambridge Univ. Press, Cambridge (2005)
- × Demaine, E.D., O'Rourke, J.: Geometric Folding Algorithms. Cambridge University Press, Cambridge (2007) (Linkages, origami, polyhedra)
- × DeMarco, L.: Dynamics of rational maps: Lyapunov exponents, bifurcations, and capacity. Math. Ann. 326 (1), 43--73 (2003)
- × Duren, P.L.: Univalent functions. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 259. Springer, New York (1983)
- × Forn[U+00E6]ss, J.E., Sibony, N.: Complex dynamics in higher dimensions. In: Complex Potential Theory (Montreal, PQ, 1993), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., vol. 439, pp. 131--186. Kluwer Acad. Publ., Dordrecht (1994) (Notes partially written by Estela A. Gavosto)
- × Freire, A., Lopes, A., Ma~né, R.: An invariant measure for rational maps. Bol. Soc. Brasil. Mat. 14 (1), 45--62 (1983)
- × Hubbard, J., Papadopol, P.: Superattractive fixed points in $ { c}^n$. Indiana Univ. Math. J. 43 , 321--365 (1994)
- × Hubbard, J.H.: Teichm[U+00A8]uller theory and applications to geometry, topology, and dynamics, vol. 1. Matrix Editions, Ithaca (2006). Teichm[U+00A8]uller theory, with contributions by Adrien Douady, William Dunbar, Roland Roeder, Sylvain Bonnot, David Brown, Allen Hatcher, Chris Hruska and Sudeb Mitra, with forewords by William Thurston and Clifford Earle
- × Ju, M.: Ljubich. Entropy properties of rational endomorphisms of the Riemann sphere. Ergodic Theory Dyn. Syst. 3 (3), 351--385 (1983)
- × Pogorelov, A.V.: Extrinsic Geometry of Convex Surfaces. American Mathematical Society, Providence (1973) (translated from the Russian by Israel Program for Scientific Translations, Translations of Mathematical Monographs, vol. 35)
- × Pommerenke, Ch.: Boundary Behaviour of Conformal Maps. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 299. Springer, Berlin (1992)
- × Rešetnjak, Ju.G.: Isothermal coordinates on manifolds of bounded curvature. I, II. Sibirsk. Mat. [U+02C7]Z. 1 , 88--116, 248--276 (1960)
- × Reshetnyak, Yu.G.: Two-dimensional manifolds of bounded curvature. In: Geometry, IV, Encyclopedia Math. Sci., vol. 70 , pp. 3--163, 245--250. Springer, Berlin (1993)
- × Series, C.: Thurston's bending measure conjecture for once punctured torus groups. In: Spaces of Kleinian Groups, London Math. Soc. Lecture Note Ser., vol. 329, pp. 75--89. Cambridge Univ. Press, Cambridge (2006)
- × Spivak, M.: A Comprehensive Introduction to Differential Geometry, vol. II, 2nd edn. Publish or Perish Inc, Wilmington (1979)
- × Thurston, W.P.: Shapes of polyhedra and triangulations of the sphere. In: The Epstein Birthday Schrift, Geom. Topol. Monogr., vol. 1, pp. 511--549. Geom. Topol. Publ., Coventry (1998)
- × The Sage Developers. Sage Mathematics Software (Version 6.10.beta7) (2016).
- × Van Andel, E., Bradshaw, R.: Riemann mapping [sage mathematics software package] (2011)