In Sect. 2 we explain our motivations to study Question 1.1. In Sect. 3 we prove assertions (1) and (2) of Theorem 1.5, and in Sect. 4 we prove assertion (3). Theorem 4.1 gives the general construction of our counterexamples to Question 1.4 for $ n = 3$, and Example 4.2 contains a simple example. Appendix A gives an informal introduction to key forms used in the proof of Theorem 4.1, and Appendix B contains the proof of a technical result used in the proof of Theorem 4.1.

Our original motivation to study Question 1.1 comes from construction of projective compactifications of $ \cc^n$ via degree-like functions . More precisely, given an affine variety $ X$ over a field $ \kk$, a degree-like function on the ring $ \kk[X]$ of regular functions on $ X$ is a map $ \delta: \kk[X] \to \zz \cup \{-\infty\}$ which satisfies the following properties satisfied by the degree of polynomials:

1. (i) $ \delta(\kk) = 0$,
2. (ii) $ \delta(fg) \leq \delta(f) + \delta(g)$,
3. (iii) $ \delta(f+g) \leq \max\{\delta(f), \delta(g)\}$.

   The graded ring associated with $ \delta$ is

   \begin{align} \kxdelta &:= \dsum_{d \geq 0} \{f \in \kk[X]: \delta(f) \leq d\} \nonumber\\ &\cong \sum_{d \geq 0} \{f \in \kk[X]: \delta(f)\leq d\}t^d \subseteq \kk[X][t] \label{kxdelta} \end{align}

   (2.1)

   where $ t$ is an indeterminate. If $ \delta$ satisfies the following properties:
4. (iv) $ \delta(f) > 0$ for all non-constant $ f$, and
5. (v) $ \kxdelta$ is a finitely generated $ \kk$-algebra,

It is straightforward to check that the maximum of finitely many degree-like functions is also a degree-like function, and taking the maximum is one of the basic ways to construct new degree-like functions (see e.g. [Mondal2014], Theorem 4.1). For example, an $ n$-dimensional convex polytope $ \scrP \subset \rr^n$ with integral vertices and containing the origin in its interior determines a degree-like function on $ \kk[x_1, x_1^{-1}, \ldots, x_n, x_n^{-1}]$ defined as follows: \begin{eqnarray*} \delta_\scrP\left(\sum a_\alpha x^\alpha\right) := \inf\{d\in \zz: d \geq 0,\ \alpha \in d\scrP\ \text{for all}\ \alpha \in \zz^n\ \text{such that}\ a_\alpha \neq 0\} \end{eqnarray*} It is straightforward to see that $ \delta_\scrP$ satisfies properties (iv) and (v), so that it determines a projective completion $ X_\scrP$ of the torus $ \nktorus$. It turns out that $ X_\scrP$ is precisely the toric variety corresponding to $ \scrP$. Moreover, $ \delta_\scrP$ is the maximum of some other 'simpler' degree-like functions determined by facets of $ \scrP$—see Fig. 1 for an example.

Figure 1 $ \delta_\scrP = \max\{\delta_1, \delta_2, \delta_3\}$.

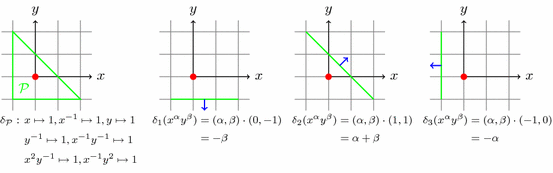
The preceding discussion suggests that the following is a fundamental question in the theory of degree-like functions:

In the scenario of Question 2.1, identifying $ \kxdeltaone$ and $ \kxdeltatwo$ with subrings of $ \kk[X][t]$ as in (2.1) implies that $ \kxdelta = \kxdeltaone \cap \kxdeltatwo$. Consequently, in the case that $ \kk = \cc$ and $ X$ is the affine space $ \cc^n$, Question 2.1 is a special case of Question 1.1, and our counterexamples to Question 1.4 are in fact counterexamples to this special case with $ X = \cc^2$.

Given a closed subset $ S$ of $ \rr^n$, the $ S$-moment problem asks for characterization of linear functionals $ L$ on $ \rr[x_1, \ldots, x_n]$ such that $ L(f)= \int_S f\, \mathrm{d} \mu$ for some (positive Borel) measure $ \mu$ on $ S$. Classically the moment problem was considered on the real line ($ n = 1$): given a linear functional $ L$ on $ \rr[x]$, a necessary and sufficient condition for $ L$ to be induced by a positive Borel measure on $ S \subseteq \rr$ was shown to be

• $ L(f^2 + xg^2) \geq 0$ for all $ f,g \in \rr[x]$ in the case that $ S = [0, \infty)$ ([Stieltjes1895]);
• $ L(f^2) \geq 0$ for all $ f\in \rr[x]$ in the case that $ S = \rr$ ([Hamburger1921]);
• $ L(f^2 + xg^2 + (1-x)h^2) \geq 0$ for all $ f,g,h \in \rr[x]$ in the case that $ S = [-1,1]$ ([Hausdorff1921]).

In particular, the classical examples show that $ \emptyset$, $ \{x\}$, $ \{x, 1 - x\}$ solves the moment problem respectively for $ \rr$, $ [0, \infty)$, $ [0, 1]$. In the case that $ S$ is a basic semialgebraic set, i.e. $ S$ is defined by finitely many polynomial inequalities $ f_ 1 \geq 0, \ldots, f_s \geq 0$, [Schmüdgen1991] proved that $ \{f_1, \ldots, f_s\}$ solves the $ S$-moment problem provided $ S$ is compact. On the other hand, if $ S$ is non-compact, then it may happen that no finite set of polynomials solves the moment problem for $ S$ (see e.g. [Kuhlmann and Marshall2002], [Powers and Scheiderer2001]). Netzer associated (see e.g. [Mondal and Netzer2014], Section 1) a natural filtration $ \{\scrB_d(S): d \geq 0\}$ on the polynomial ring determined by $ S$: \begin{align*} \scrB_d(S) &:= \{f \in \rr[x_1, \ldots, x_n]: f^2 \leq g\ \text{on}\ S\ \text{for some}\ g \in \rr[x_1, \ldots, x_n],\\ &\quad\ \deg(g) \leq 2d\} \end{align*} In other words, $ \scrB_d(S)$ is the set of all polynomials which 'grow on $ S$ as if they were of degree at most $ d$'. The graded algebra corresponding to the filtration is \begin{align*} \scrB(S) := \dsum_{d \geq 0} \scrB_d(S) \cong \sum_{d \geq 0} \scrB_d(S)t^d \subseteq \rr[x_1, \ldots, x_n, t] \end{align*} where $ t$ is a new indeterminate.

It is straightforward to produce open semialgebraic sets $ S$ which satisfies the assumption of Theorem 2.3. E.g. a standard tentacle is a set \begin{eqnarray*} \left\{ (\lambda^{\omega_1}b_1,\ldots,\lambda^{\omega_n}b_n)\mid \lambda \in \rr, \lambda \geq 1, b\in B\right\} \end{eqnarray*} where $ \omega := (\omega_1, \ldots, \omega_n) \in \zz^n$ and $ B\subseteq (\rr{\setminus}\{0\})^n$ is a compact semialgebraic set with nonempty interior; we call $ \omega$ the weight vector corresponding to the tentacle. If $ S$ is a finite union of standard tentacles with weights $ \omega_1, \ldots, \omega_k \in \zz^n$, then it is not too hard to see that

• $ \scrB_0(S) = \rr$ iff the cone $ \{\lambda_1 \omega_1 + \cdots + \lambda_k \omega_k : \lambda_1, \ldots, \lambda_k \geq 0\}$ is all of $ \rr^n$, and
• $ \scrB(S)$ is finitely generated over $ \rr$.

Figure 2 $ S = S_+ \cup S_-$, where $ S_+ = \{(x,y) \in \rr^2: x \geq 1,\ 0.5 \leq x^3(y - x^3 - x^{-2}) \leq 2\}$ and $ S_- = \{(x,y) \in \rr^2: x \geq 1,\ 0.5 \leq x^3(y + x^3 - x^{-2}) \leq 2\}$.

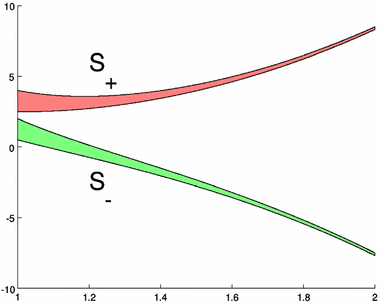
Let $ p, q_1, \ldots, q_k, \omega_1, \omega_2$ be as in conditions (A)–(D) of Sect. 4.1. Pick nonzero $ a_1, \ldots, a_k \in \rr$ and define $ f_+(x), f_-(x)$ as in (4.1) and (4.2) . Note that as opposed to Sect. 4.1, here $ f_+(x)$ and $ f_-(x)$ are polynomials over real numbers . For each $ i \in \{+,-\}$, pick positive real numbers $ c_{i,1} < c_{i,2}$ and define \begin{align*} S_i := \{(x,y) \in \rr^2: x \geq 1,\ c_{i,1} \leq x^{\omega_2/\omega_1} ( y - f_i(x)) \leq c_{i,2}\} \end{align*} Let $ \delta_+, \delta_-, R_+, R_-$ be as in Sect. 4.1. For $ i \in \{+,-\}$, [Mondal and Netzer2014] ([Mondal and Netzer2014], Lemma 4.3) implies that $ f(x,y) \in \scrB_d(S_i)$ iff $ \delta_i(f) \leq p\omega_1d$. It follows that the map $ \phi: t \mapsto t^{p\omega_1}$ maps $ \scrB(S_i) \into R_i$. It is straightforward to check that $ R_+, R_ -, R_+ \cap R_-$ are integral over $ \scrB(S_+), \scrB(S_-), \scrB(S_+) \cap \scrB(S_-)$ respectively. Lemma 3.2 and Theorem 4.1 then imply that $ \scrB(S_+)$ and $ \scrB(S_-)$ are finitely generated over $ \rr$, but $ \scrB(S_+ \cup S_-) = \scrB(S_-) \cap \scrB(S_+)$ is not, even though $ \scrB_0(S_+ \cup S_-) = \rr$. Figure 2 depicts a pair of $ S_+$ and $ S_-$ corresponding to Example 4.2.

Assume w.l.o.g. $ \trdeg_\cc(L) = 1$. Theorem 3.3 implies that $ R'_1$ is finitely generated as a $ \cc$-algebra. Let $ C$ be the unique non-singular projective curve over $ \cc$ such that the field of rational functions on $ C$ is $ L$. Then $ C'_1 := \spec R'_1$ is isomorphic to $ C {\setminus} \{x_1, \ldots, x_k\}$ for finitely many points $ x_1, \ldots, x_k \in C$. Then the local rings $ \sheaf_{C,x_j}$ of $ C$ at $ x_j$'s are the only one dimensional valuation rings of $ L$ not containing $ R'_1$. Let $ \bar R$ be the integral closure of $ R$ in $ L$. Since $ \bar R \subseteq R'_1$, Lemma 3.1 implies that \begin{eqnarray*} \bar R = R'_1 \cap \sheaf_{C,x_{j_1}} \cap \cdots \cap \sheaf_{C,x_{j_s}} \end{eqnarray*} for some $ j_1, \ldots, j_s \in \{1, \ldots, k\}$. Then $ \bar R$ is the ring of regular functions on $ C {\setminus} \{x_j: j\not\in \{j_1, \ldots, j_s\}\}$, and is therefore finitely generated over $ \cc$. Lemma 3.2 then implies that $ R$ is finitely generated over $ \cc$.

Let $ L$ be the field of fraction of $ R$. Due to assertion (1) we may assume $ \trdeg_\cc(L) = 2$. Theorem 3.3 implies that $ R'_1$ and $ R'_2$ are finitely generated over $ \cc$. Let $ X_i := \spec R'_i$ and $ \bar X_i$ be a projective compactification of $ X_i$, $ i = 1,2$. Let $ \bar X$ be the closure in $ \bar X_1 \times \bar X_2$ of the graph of the birational correspondence $ X_1 \dashrightarrow X_2$ induced by the identification of their fields of rational functions, and $ \tilde X$ be the normalization of $ \bar X$. For each $ i$, let $ \pi_i: \tilde X \to \bar X_i$ be the natural projection and set $ U_i := \pi_i^{-1}(X_i)$.

Proof.

The assumption that $ R_i$'s are integrally closed together with Claim 3.5 and Theorem 3.4 imply that $ R = R'_1 \cap R'_2 = \Gamma(U_1 \cup U_2, \sheaf_{\tilde X})$ is finitely generated over $ \cc$, as required. $ \square$

Let $ p, q_1, \ldots, q_k$ be integers such that

1. (A) $ p$ is an odd integer $ \geq 3$,
2. (B) $ 0 \leq q_1 < q_2 < \cdots < q_k < p$,
3. (C) there exists $ j$ such that $ q_j$ is positive and even,

   and let $ \omega_1,\omega_2$ be relatively prime positive integers such that

4. (D) $ p \geq \omega_2/\omega_1 > q_k$.

Assertion (3) of Theorem 1.5 follows from Theorem 4.1 below.

We prove assertion (1) of Theorem 4.1 only for $ R_+$, since the statement for $ R_-$ follows upon replacing each $ a_j$ to $ (-1)^{q_j}a_j$.

The fact that $ R_+$ is integrally closed follows from the observation that $ \delta_+(g^k) = k\delta_+(g)$ for each $ g \in \cc[x,y]$ and $ k \geq 0$, i.e. $ \delta_+$ is a subdegree in the terminology of [Mondal2010] (see e.g. [Mondal2010], Proposition 2.2.7). We give a proof here for the sake of completeness.

Proof.

Lemma 4.4 shows that $ \Rplus$ is integrally closed. Now we show that $ \Rplus$ is finitely generated over $ \cc$. Set $ q_0 := 0$ and define

Proof.

Proof.

Since $ \Gamma$ is a finitely generated subsemigroup of $ \zz^{k+3}$, Corollary 4.7 proves assertion (1) of Theorem 4.1.

Let $ u,v, \xi$ be indeterminates. Let

Now note that \begin{align*} v^2|_{v = \phi(u,\xi)} &= u^p + 2a_1u^{(p-q_1)/2} + \cdots + 2a_ku^{(p-q_k)/2} + 2\xi u^{p/2 - \omega_2/(2\omega_1)} + \ldt \end{align*} where $ \ldt$ denotes terms with degree in $ u$ smaller than \begin{eqnarray*} \epsilon := p/2 - \omega_2/(2\omega_1) \end{eqnarray*} Note that $ \epsilon \geq 0$ due to defining property (D) of $ \omega_1, \omega_2$. Define

1. (a) $ \eta(h_0) > \eta(h_1) > \cdots > \eta(h_k) = 2\omega_1\epsilon \geq 0$.
2. (b) $ h_k|_{v = \phi(u,\xi)} = 2\xi u^\epsilon + $ terms with degree in $ u$ smaller than $ \epsilon$.

   It then follows that $ u, v, h_0, \ldots, h_k$ is the sequence of key forms of $ \eta$—see Appendix A for an informal discussion of key forms, and ([Mondal2016a], definition 3.16) for the precise definition. Property (C) of $ q_1, \ldots, q_k$ implies that $ h_k$ is not a polynomial. This, together with observation (a) and [Mondal and Netzer2014] ([Mondal and Netzer2014], theorem 4.13 and proposition 4.14) implies (see Appendix A.4) that

3. (c) $ \cc[u,v]^\eta$ is not finitely generated over $ \cc$,
4. (d) $ \eta(f) > 0$ for each $ f \in \cc[u,v] {\setminus} \cc$,
5. (e) if $ \epsilon > 0$, then $ \{f \in \cc[u,v]: \eta(f) \leq d \}$ is a finite dimensional vector space over $ \cc$ for all $ d \geq 0$,
6. (f) if $ \epsilon = 0$, then there exists $ d > 0$ such that $ \{f \in \cc[u,v]: \eta(f) \leq d \}$ is an infinite dimensional vector space over $ \cc$.

Since $ R = \cxydelta$ is integral over $ \cc[u,v]^\eta$, observations (c)–(f) imply assertions (2)–(5) of Theorem 4.1. $ \square$