Received: 19 December 2016 / Accepted: 27 July 2017
Abstract
Keywords
Thurston map, Branched covering, Teichmüllertheory, Self-similar groupMathematics Subject Classification
Primary 37F10; Secondary 57M12, 30F60
1. Introduction

Complex dynamics studies iteration of rational functions $ f: \rs \to \rs$. An important subclass consists of the postcritically finite rational maps: those for which the postcritical set $ P(f):=\cup_{n> 0}f^{\circ n}(C(f))$ is finite; here $ C(f)$ is the finite set of points at which $ f$ is not locally injective. For example, if $ c_R \in \Csps$ is the unique root of $ c^3+2c^2+c+1$ with $ \Im(c_R)> 0$, then the quadratic polynomial $ f(z)=z^2+c_R$, known as Douady's rabbit , is postcritically finite: it has one fixed critical point at infinity, and the unique finite critical point at the origin is periodic of period 3. Another example is provided by $ f(z)=z^2+i$. The Julia sets of these maps are shown in Fig. 1. Their three finite postcritical points are marked with tiny circles.
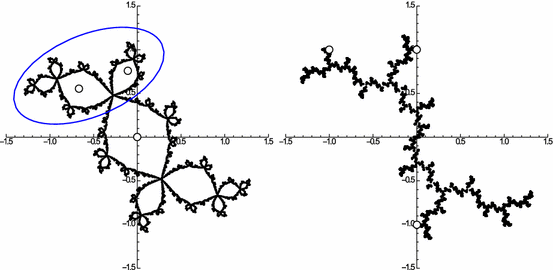
Thurston Maps. A Thurston map is a continuous, orientation-preserving branched covering $ f:S^2\to S^2$ of degree at least two for which the set $ P(f)$ is finite. For example, if $ h$ is a Dehn twist about the blue ellipse in Fig. 1, one may twist Douady's rabbit by post-composing $ f$ with $ h$ to yield a Thurston map $ g=h\circ f$. More generally, if $ h_0, h_1\co S^2\to S^2$ are orientation-preserving homeomorphisms such that $ h_0$ agrees with $ h_1^{-1}$ on $ P(f)$ , then we call $ h_0 \circ f \circ h_1$ a twist of $ f$. We call the resulting collection of maps the pure Hurwitz class of $ f$. See Sect. 4 for related definitions and discussion.
Combinatorial Equivalence. Two Thurston maps $ f, g$ are combinatorially equivalent or Thurston equivalent if there are orientation-preserving homeomorphisms $ h_0, h_1: (S^2, P(f)) \to (S^2, P(g))$ for which $ h_0 \circ f = g \circ h_1$ and $ h_0, h_1$ are isotopic through homeomorphisms agreeing on $ P(f)$. More succinctly: they are conjugate up to isotopy relative to their postcritical sets. This is related to a more familiar notion. For a finite set $ P \subset S^2$, denote by $ \PMod(S^2, P)$ the pure mapping class group of the pair $ (S^2,P)$. Suppose $ P(f)=P(g)=P$. The notion of combinatorial equivalence between $ f$ and $ g$ is analogous to the notion of conjugacy in $ \PMod(S^2, P)$, but now the representing maps are branched coverings instead of homeomorphisms.
W. Thurston's Characterization of Rational Maps. W. Thurston ([Douady and Hubbard1993]) gave necessary and sufficient combinatorial conditions for a Thurston map $ f$ to be equivalent to a rational map $ g$. The statement has two cases, depending on the Euler characteristic $ \chi(\mathcal{O}(f))$ of a certain orbifold structure $ \mathcal{O}(f)$ on the sphere associated to the dynamics of $ f$ on the set $ P(f) \cup C(f)$; see [Douady and Hubbard1993]. Typical Thurston maps have hyperbolic orbifold ($ \chi< 0$) and checking rationality involves ruling out certain families of curves, called obstructions . Atypical Thurston maps have Euclidean orbifold ($ \chi=0$)—we call these Euclidean —and checking rationality involves examining the eigenvalues of a two by two matrix. Apart from a well-understood subset of Euclidean maps known as flexible rational Lattès maps , the rational map $ g$ equivalent to a Thurston map $ f$, if it exists, is unique up to holomorphic conjugacy.
Checking that there are no obstructions is often very difficult. To give a sense of the complexity that can occur, consider the following result, Theorem 1. All of the maps involved are typical NET maps—the special class of Thurston maps that is the focus of this paper.
Theorem 1.
Each twist of the rabbit $ f(z)=z^2+c_R$ is combinatorially equivalent to a complex polynomial $ z^2+c$ where $ c^3+2c^2+c+1=0$; all three cases arise. In contrast, for twists of $ f(z)=z^2+i$, the problem of determining rationality of a twist $ h\circ f$ reduces to checking the image of $ h$ under a homomorphism to a finite group of order $ 100$. Among these combinatorial classes there are precisely two classes of rational maps, namely $ z \mapsto z^2\pm i$, and a countably infinite family of pairwise inequivalent twists of the form $ h^n\circ g, n \in \Z$, where $ g$ is a particular obstructed twist and $ h$ is a Dehn twist about the obstruction of $ g$.The first statement follows from a general result now known as the Berstein-Levy theorem ([Levy1985]), while the second is more recent and is one of the main results of Bartholdi and Nekrashevych's article ([Bartholdi and Nekrashevych2006], [U+00A7]6).
When all twists of $ f$ are equivalent to rational maps, we say its pure Hurwitz class is completely unobstructed . Some pure Hurwitz classes are completely obstructed (defined analogously) and some are neither, i.e. contain both obstructed and unobstructed maps.
Induced Dynamics on Curves. A simple closed curve in $ S^2-P(f)$ is essential if it is not freely homotopic to a constant curve at a point in $ S^2-P(f)$. An essential curve is peripheral if it is homotopic into arbitrarily small neighborhoods of a point of $ P(f)$. A Thurston map $ f$ and all its iterates are unramified outside the set $ P(f)$, so curves in $ S^2-P(f)$ can be iteratively lifted under $ f$. For example, it is easy to see that under iterated pullback the blue ellipse $ \gamma$ in Fig. 1 is periodic of period 3 up to homotopy, and that $ \deg(f^3: \tilde{\gamma} \to \gamma)=4$, where $ \tilde{\gamma}$ is the unique preimage of $ \gamma$ under $ f^{3}$ that is essential and nonperipheral in $ S^2-P(f)$. There are countably infinitely many simple closed curves up to homotopy in $ S^2-P(f)$, though, and it is harder to see the following:
Theorem 2.
([Pilgrim2012], Theorem 1.6) Under iterated pullback of the rabbit polynomial $ f(z)=z^2+c_R$, any simple closed curve becomes either inessential or peripheral in $ S^2-P(f)$ or, up to homotopy, falls into the above 3-cycle.See the end of Sect. 7 for an outline of another way to prove this result.
Focusing on the behavior of curves under pullback is important. The statement of W. Thurston's characterization theorem for rational maps among Thurston maps says that obstructions to $ f$ being rational are multicurves $ \Gamma \subset S^2-P(f)$ with a certain invariance property. Specifically: after deleting inessential and peripheral preimages, we have $ f^{-1}(\Gamma)\subset \Gamma$ up to homotopy in $ S^2-P(f)$, and the spectral radius of a certain associated linear map $ f_\Gamma: \R^\Gamma \to \R^\Gamma$ is greater than or equal to $ 1$.
Teichmüller Theory. The proof of W. Thurston's characterization theorem reduces the question "Is $ f$ equivalent to a rational map?" to the problem of finding a fixed point for a certain holomorphic self-map $ \sigma_f: \Teich(S^2, P(f)) \to \Teich(S^2, P(f))$ of a Teichmüller space, given by pulling back complex structures under $ f$; see [Douady and Hubbard1993]. For the precise definition of $ \sigma_f$, we refer the reader to [Buff et al.2009]. Although $ \sigma_f$ is complicated and transcendental, it covers a finite algebraic correspondence on moduli space:
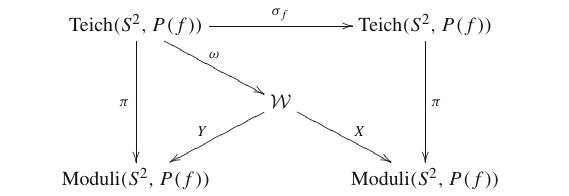
See [Koch2013] and [Koch et al.2016]. In the above diagram, $ Y$ is a finite covering, $ X$ is holomorphic, and only $ \sigma_f$ depends on $ f$; up to isomorphism induced by conjugation by impure mapping class elements, the remainder depends only on the pure Hurwitz class of $ f$, cf. [Koch2013] and [Koch et al.2016] ([Koch et al.2016], [U+00A7]3). In the case of the rabbit, the moduli space is isomorphic to $ \IP^1-\{0,1,\infty\}$, the map $ X$ is injective, so that we may regard $ \mathcal{W} \subset \IP^1-\{0,1,\infty\}$, the map $ Y$ is given by $ x \mapsto 1-\frac{1}{x^2}$, and $ \mathcal{W}=\IP^1-\{\pm 1, 0,\infty\}$; see [Bartholdi and Nekrashevych2006]. For quadratics with four postcritical points and hyperbolic orbifold, $ X$ is always injective, and the formulas for $ Y \circ X^{-1}$ are quite simple. For other maps, the equations defining the correspondence $ \mathcal{W}$ may be complicated. This happens even for maps with four postcritical points, including Euclidean quadratics, many cubics, and most NET maps.
Of special interest is the group $ G_f < \PMod(S^2,P(f))$ represented by liftable homeomorphisms $ h$, i.e. those for which there is a lift $ \tilde{h}$ representing an element in $ \PMod(S^2, P(f))$ with $ h\circ f = f \circ \tilde{h}$; the assignment $ h \mapsto \tilde{h}$ gives a homomorphism $ \phi_f: G_f \to \PMod(S^2, P(f))$ which we call the virtual endomorphism on $ \PMod(S^2, P(f))$. If there is a fixed point $ \tau$ of $ \sigma_f$, and if $ w:=\omega(\tau), m:=Y(w)=X(w)$, then $ \phi_f = X_*\circ Y^{-1}_*$ is the induced map on fundamental groups based at these points. The domain of $ \zf_f$ is the subgroup $ Y_*(\pi_1(\mathcal{W}),w)$.
Nearly Euclidean Thurston Maps. The family of nearly Euclidean Thurston (NET) maps, introduced in [Cannon et al.2012], provides an extremely rich family of simple examples of Thurston maps for which explicit algorithmic computations are possible. By definition, a Thurston map $ f$ is NET if (1) each critical point has local degree 2, and (2) $ \#P(f)=4$. So, both $ z \mapsto z^2+c_R$ and $ z \mapsto z^2+i$ are NET maps. A NET map is Euclidean if and only if $ P(f) \cap C(f)=\emptyset$. One thing that makes NET maps so interesting is that each NET map $ f$ admits what we call a NET map presentation . This means that $ f$ is combinatorially equivalent to a map in a very special normal form. See Sect. 3. Conversely, a NET map presentation defines a combinatorial equivalence class of NET maps.
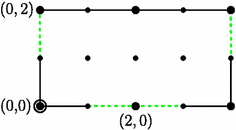
NET Map Presentation for the Rabbit. Figure 2 shows a NET map presentation diagram for the rabbit $ f(z)=z^2+c_R$. With some conventions understood, it is remarkably simple. Here are the details.
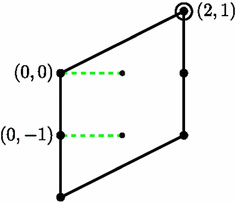
Let $ \Lambda_2=\mathbb{Z}^2$, and let $ \Lambda_1< \Lambda_2$ be the lattice generated by $ (0,-1)$ and $ (2,1)$. For $ i=1,2$ let $ \Gamma_i$ be the groups generated by 180$ ^\circ$ rotations about the elements of $ \Lambda_i$, and let $ S^2_i = \R^2/\Gamma_i$ be the quotient. A fundamental domain for $ \Gamma_1$ is shown in Fig. 2. Since $ \Gamma_1 < \Gamma_2$ there is an "origami" quotient map $ \overline{id}: S^2_1 \to S^2_2$. Let $ A=\left[\begin{smallmatrix}0 & 2 \\ -1 & 1 \end{smallmatrix}\right]$, $ b=\left[\begin{smallmatrix}2 \\ 1\end{smallmatrix}\right]$ and $ \Phi: \R^2 \to \R^2$ be the affine map $ \zF(x)=Ax+b$. The columns of $ A$ are our lattice generators, and $ b$ is the circled lattice point in Fig. 2. The map $ \zF$ induces an affine homeomorphism $ \overline{\Phi}:S^2_2 \to S^2_1$. We set $ g=\overline{\Phi}\circ\overline{id}$; it is an affine branched cover of $ S^2_1$ to itself. Finally, we put $ f=h\circ g$ where $ h: S^2_1 \to S^2_1$ is a point-pushing homeomorphism along the indicated green (dashed horizontal) segments in Fig. 2. Figure 2 completely describes this Thurston map up to combinatorial equivalence.
Computations for NET Maps. If $ f$ is a NET map, then $ \#P(f)=4$. This makes things much easier than for general Thurston maps. After some natural identifications, we have the following.
- (1) The Teichmüller space $ \Teich(S^2, P(f))$ is the upper half-plane $ \IH \subset \Csps$.
- (2) The pure and ordinary mapping class groups $ \PMod(S^2, P(f))$ and $ \Mod(S^2, P(f))$ are the congruence subgroup $ \PGamma(2)$ and $ \PSL(2,\Z)\ltimes (\Z/2\Z\times\Z/2\Z)$ respectively.
- (3) The domain of the correspondence $ \mathcal{W}$ is a classical modular curve (see Sect. 4).
- (4) The map $ Y:\mathcal{W}\to \mathrm{Moduli}(S^2,P(f))$ extends to a Belyi map $ \overline{Y}:{\overline{\mathcal{W}}}\to \mathbb{P}^1$.
- (5) The homotopy classes of curves in $ S^2-P(f)$ are classified by their slopes, that is, elements of $ \Qbar = \Q \cup \{\pm 1/0=\infty\}$; with conventional identifications, each slope $ p/q$ corresponds to the ideal boundary point $ -q/p \in \partial \IH$.
- (6) By taking preimages of curves, we obtain a slope function $ \mu_f: \Qbar \to \Qbar \cup \{\odot\}$ where $ \odot$ denotes the union of inessential and peripheral homotopy classes; this encodes the Weil–Petersson boundary values of $ \sigma_f$, shown to exist in general by [Selinger2012]. More precisely, if $ \frac{p}{q}\in \overline{\Q}$ and $ \zs_f(-\frac{q}{p})\in \overline{\Q}$, then $ \zm_f(\frac{p}{q})=-\zs_f(-\frac{q}{p})^{-1}$. If $ \zs_f(-\frac{q}{p})\notin \overline{\Q}$, then $ \zm_f(\frac{p}{q})=\odot$.
- (7) Varying the choice of translation term $ b$ does not affect the fundamental invariants, such as $ \zs_f$ above, or the ones given below in Theorem 3 (so long as such choices result in maps with four postcritical points, which is almost always the case). Thus virtual NET map presentation diagrams , in which the translation term is omitted, suffice to compute such invariants.
Since NET maps are very close to affine maps, it turns out that explicit computations of what happens to slopes under pullback are possible.
Theorem 3.
([Cannon et al.2012], Theorems 4.1, 5.1, 5.3) Given a NET map presentation for a Thurston map $ f$ and the slope $ p/q$ of a curve $ \gamma$, there is an algorithm which computes- (1) $ c_f(p/q)=$ the number of essential and nonperipheral preimages $ \tilde{\gamma}_1, \ldots, \tilde{\gamma}_c \subset f^{-1}(\gamma)$,
- (2) $ d_f(p/q)=$ the common degree by which these preimages map onto $ \gamma$, and
- (3) $ \mu_f(p/q)=$ the slope of the common homotopy class of the preimages $ \tilde{\gamma}_i$.
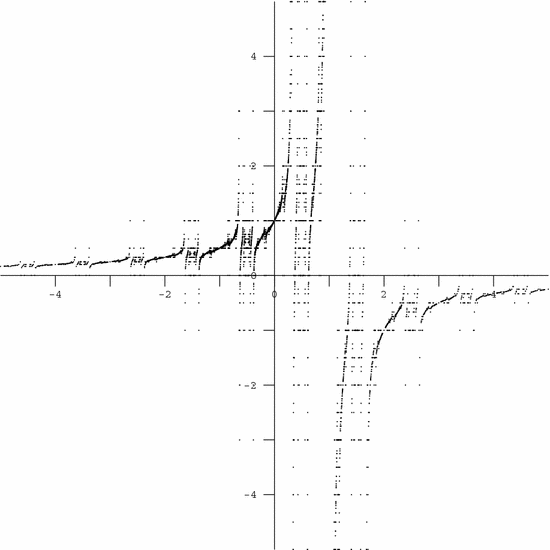
The behavior of the slope function $ \mu_f$ is rather intricate. For the rabbit, Fig. 3 is a plot of the values $ \zm_f(\frac{p}{q})$ with $ \left|p\right|\le 50$ and $ 0\le q\le 50$. In fact, the closure of this graph is all of $ \R^2$.
The multiplier of $ p/q$ under $ f$ is $ \delta_f(p/q)=c_f(p/q)/d_f(p/q)$. When $ \#P(f)=4$, W. Thurston's characterization theorem reduces to the following. A Thurston map $ f$ with hyperbolic orbifold is obstructed if and only if there exists a slope $ p/q$ for which $ \mu_f(p/q)=p/q$ and $ \delta_f(p/q) \geq 1$. It turns out that knowledge of data points of the form $ (p/q, p'/q', \delta_f(p/q))$, where $ p'/q'=\mu_f(p/q)$, restricts the possible slopes of such obstructions:
Theorem 4.
(Half-Space Theorem ([Cannon et al.2012], Theorem 6.7)) Suppose $ p'/q'=\mu_f(p/q) \neq p/q$ or $ \odot$. There is an algorithm that takes as input the triple $ (p/q, p'/q', \delta_f(p/q))$ and computes as output an excluded open interval $ J=J(p/q, p'/q', \delta_f(p/q)) \subset \Qbar$ containing $ -q/p$ such that no point of $ J$ is the negative reciprocal of the slope of an obstruction.The intervals in Theorem 4 are obtained from half-spaces in $ \IH$. The boundary of a half-space in $ \IH$ has a finite part, consisting of points in $ \IH$, and an infinite part, consisting of points in $ \partial \IH$. The intervals in Theorem 4 are the infinite boundary points of half-spaces in $ \IH$ minus endpoints. Figure 4 shows the deployment of some of the half-spaces (in grey, with black boundaries, $ |p|\le 25$, $ |q|\le 25$) for these excluded intervals in the case of the presentation of the rabbit in Fig. 2.

It may happen that for some finite set $ \{p_1/q_1, \ldots, p_m/q_m\}$ the associated excluded intervals cover all of $ \Qbar$. This implies that there are no obstructions and therefore, by W. Thurston's characterization theorem, $ f$ is equivalent to a rational map. As indicated by Fig. 4, finitely many excluded intervals cover $ \overline{\mathbb{Q}}$ for the rabbit. In fact, careful inspection shows that three half-spaces suffice. An extension of this theorem to the case when $ \mu_f(p/q)=p/q$ or $ \odot$ is described in Sect. 8. See the discussion of Sect. 8 in the introduction below.
Parry with assistance from Floyd has written and continues to improve a computer program NETmap which computes information like the above for a given NET map. Figures 3 and 4 are part of this program's output for the rabbit with the presentation in Fig. 2. That it can do what it does illustrates the tractability of NET maps. Executable files, documentation and more can be found at the [NET maps2016] website.
Summary. Here is a summary of this article.
Findings (Sect. 2). We briefly report on the phenomena observed among the NET maps we have investigated.
NET map presentations (Sect. 3). This section explains presentations of general NET maps of the type given above for the rabbit.
Hurwitz classes (Sect. 4). We first briefly recall some terminology and facts related to Hurwitz classes. We present invariants of Hurwitz classes of NET maps, in particular, a complete set of invariants for impure Hurwitz classes of NET maps. For NET maps, an impure Hurwitz class consists either entirely of Euclidean maps, or of non-Euclidean maps.
Parry has written a computer program which enumerates these impure Hurwitz class invariants and outputs one representative virtual NET map presentation for every impure Hurwitz class of NET maps. For the definition of NET map presentation, see Sect. 3. It organizes these virtual NET map presentations by elementary divisors. (See the discussion of Hurwitz invariants in Sect. 4 for the definition of their elementary divisors.) The NET map web site ([NET maps2016]) contains a catalog of these representative NET map presentations through degree 30. It also contains NETmap's output for every such example. We use the notation $ mn$HClass$ k$ to denote the $ k$th virtual NET map presentation with elementary divisors $ m$ and $ n$ in this catalog.
We prove the following theorem.
Theorem 5.
Suppose $ f$ is a non-Euclidean NET map and $ \HHH$ its impure Hurwitz class. There is an algorithm which computes the image of $ \delta_f$. This image $ \delta(\HHH)$ depends only on $ \HHH$ and not on the choice of representative $ f$. Furthermore:- (1) $ \delta(\HHH)=\{0\} \iff \sigma_f$ is constant;
- (2) $ \delta(\HHH) \subset [0,1)\iff \HHH$ is completely unobstructed;
- (3) $ \delta(\HHH)\ni 1 \iff \HHH$ contains infinitely many distinct combinatorial classes.
There are analogous statements for general Thurston maps and pure Hurwitz classes.
We discuss instances of statement 1 in Finding 7 of Sect. 2. We discuss instances of statement 2 in Findings 9 and 10. We discuss instances of when $ \HHH$ contains only finitely many distinct combinatorial classes in Finding 4.
In Sect. 4, we also relate the correspondence $ \cW$ to classical modular curves.
Invariants of degree 2 NET maps (Sect. 5). We discuss invariants of degree 2 NET maps. The complete classification for quadratics has recently been completed by [Kelsey and Lodge2017]. In [Floyd et al.2017b], a classification of dynamical portraits for NET maps is given; these classify the corresponding pure Hurwitz classes in degrees 2 and 3.
A conformal description of $ \zs_f$ for a degree 2 example (Sect. 6). This section demonstrates the tractability of NET maps. It illustrates how numerous invariants of NET maps can be computed by doing so for a specific example. We show for this example that the pullback map is the analytic continuation, via repeated reflection, of a conformal map between ideal hyperbolic polygons.
For this, recall that the slope function $ \mu_f$ encodes the boundary values of $ \sigma_f$, and that lifting under $ f$ determines a virtual endomorphism $ \phi_f: \PMod(S^2, P(f)) \dashrightarrow \PMod(S^2, P(f))$ with domain $ G_f$. By enlarging $ G_f$ to include reflections and so extending $ \phi_f$, and noting that reflections must lift to reflections, we can sometimes obtain detailed information about both $ \phi_f$ and $ \sigma_f$. In this way exact calculations of certain values of $ \sigma_f$ are sometimes possible. Along similar lines, a perhaps remarkable feature is that if $ \mu_{f}(p/q)=\odot$, in some circumstances, exploiting the structure of functional equations involving reflections yields exact calculations of the limiting behavior of $ \sigma_{f}(\tau)$ as $ \tau \to -q/p$ from within a fundamental domain of $ G_{f}$. This analysis is done for a particular example in Sect. 6. It is done for the rabbit near the end of Sect. 7. More generally, the pullback map of every quadratic NET map is the analytic continuation, via repeated reflection, of a conformal map between ideal hyperbolic polygons. This is also surely true of all pullback maps of cubic NET maps. In all of these cases NETmap reports that the subgroup of liftables in the extended modular group (which allows reversal of orientation) acts on $ \IH$ as a reflection group. However, there are NET maps with degree 4 (41HClass3) for which the extended modular group liftables do not act on $ \IH$ as a reflection group. This seems to be the predominant behavior in higher degrees. In such cases we do not understand the behavior of $ \zs_f$ as well.
Dynamics on curves in degree 2 (Sect. 7). Relying heavily on the results of Sect. 6, we investigate the dynamics on the set of homotopy classes of curves under iterated pullback of quadratic NET maps with one critical postcritical point. For a map $ \mu: X \to X$ from a set $ X$ to itself, we say a subset $ A$ of $ X$ is a finite global attractor if $ A$ consists of finitely many cycles into which each element $ x \in X$ eventually iterates. We show that for maps in this class that are rational, there is a finite global attractor containing at most four slopes, while for obstructed maps, there may be either (a) a finite global attractor; (b) an infinite set of fixed slopes with no wandering slopes; or (c) a finite set of fixed slopes coexisting with wandering slopes.
We remark that using techniques from self-similar groups, [Kelsey and Lodge2017] have accomplished this for all quadratic rational maps $ f$ with $ \#P(f)=4$ and hyperbolic orbifold.
The extended half-space theorem (Sect. 8). The half-space theorem, Theorem 4, applies to all extended rational numbers $ r$ which are mapped to different extended rational numbers by the Thurston pullback map $ \zs_f$ of a NET map $ f$. The half-space theorem provides an explicit interval about $ r$, called an excluded interval, which contains no negative reciprocals of slopes of obstructions for $ f$. If finitely many such excluded intervals cover a cofinite subset of $ \partial \mathbb{H}$, then we have only finitely many remaining slopes to check to determine whether $ f$ is combinatorially equivalent to a rational map.
Computations using NETmap suggest that there exist many NET maps for which every finite union of excluded intervals omits an interval of real numbers. Under suitable hypotheses, this can be proved rigorously. For example, consider the NET map $ f$ with the presentation diagram in Fig. 5. It is rational since the algorithms show $ \delta_f(p/q) \in [0,1)$ for all $ p,q$. However, one can prove that every excluded interval arising from the half-space theorem, Theorem 4, is bounded. This implies that every finite union of such intervals fails to cover all of the boundary.
One feature of the computer program NETmap is to implement a straightforward algorithm based on the extended half-space theorem. In practice, it almost always determines whether or not a NET map is, or is not, equivalent to a rational map. This leads us to
Conjecture 1.
Suppose $ f$ is a NET map. Then the extended half-space algorithm decides, in finite time, whether or not $ f$ is equivalent to a rational function.For general Thurston maps, that such an algorithm exists in theory is announced in [Bonnot et al.2012]. That such an algorithm exists in practice is announced in Bartholdi and Dudko ([Bartholdi and Dudko2017], Algorithm V.8) and indeed this is what Bartholdi's program ([Bartholdi2014]) attempts to do.
We outline a proof of the extended half-space theorem in Sect. 8.
2. Findings

We report here on many findings of interest for NET maps.
- (1) It is conjectured (see e.g. [Lodge2015], [U+00A7]9) that for non-Lattès rational maps, the pullback relation on curves has a finite global attractor. For NET maps, our evidence suggests that, more generally, this holds if there do not exist obstructions with multiplier equal to 1. The converse, however, is false. More precisely, in Sect. 7 we prove Theorem 8, which shows that a NET map $ f_0$ introduced in Sect. 6 with virtual presentation 21HClass1 is obstructed and its pullback map on curves has a finite global attractor which consists of just the obstruction. Theorem 8 also shows that there exist many obstructed maps without finite global attractors.
- (2) By perturbing flexible Lattès maps slightly within the family of NET maps, we can build examples of NET maps whose slope functions have many fixed points. By perturbing other Lattès maps, we can build examples of NET maps whose slope functions have cycles of lengths 2, 3, 4 or 6; other examples yield 5–11 and 13–15, inclusive. We do not know whether all cycle lengths occur.
- (3) There are many examples of NET maps with hyperbolic orbifolds for which no curve has all of its preimages trivial: Example 3.1 of [Cannon et al.2012]; the main example of [Lodge2015]; all NET maps in impure Hurwitz classes represented by the following virtual presentations: 22HClass6; 31HClass 5, 6, 9; 51HClass 14–16, 23, 25. This property is equivalent to surjectivity of $ X$ ([Koch et al.2016], Theorem 4.1). Indeed, among such examples there occur those whose pure (even impure) Hurwitz class is completely unobstructed (22HClass6), completely obstructed (31HClass9 with translation term $ \zl_1$), and mixed-case obstructed (Example 3.1 of [Cannon et al.2012] and the main example of [Lodge2015]).
- (4) There exist NET maps $ f$ whose impure Hurwitz class $ \HHH$ contains only finitely many Thurston equivalence classes, some of which are obstructed and some of which are not. Statement 3 of Theorem 5 shows that this is equivalent to the existence in $ \zd(\HHH)$ of some multipliers which are less than 1, some multipliers which are greater than 1 but none equal to 1. This occurs for 41HClass6, 8, 11, 19, 24.
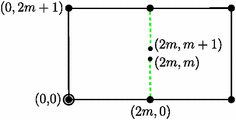
- (5) The operation of formal mating takes the dynamics of two polynomials and glues them together to form a Thurston map; see e.g. [Milnor2004]. Given a Thurston map, it might be expressible as a mating in multiple ways. The NET map of Fig. 6 arises as a mating in at least $ \zf(2m+1)$ ways, where $ \zf$ is Euler's totient function; that of Fig. 7 in at least $ m+1$ ways. This is established by showing that $ \mu_f$ has at least the corresponding number of equators —fixed-points of maximal multiplier, with the additional condition of preserving orientation—and appealing to Meyer ([Meyer2014], Theorem 4.2).
- (6) There are at least two simple
ways to create pairs of combinatorially inequivalent Thurston maps
$ f$, $ g$ for which $ \zs_f=\zs_g$:
- (a) Let $ g$ be any NET map, let $ h$ be a flexible Lattès map with $ P(h)=P(g)$ and let $ f=g\circ h$. Since $ \zs_h$ is the identity map, $ \zs_f=\zs_g$.
- (b) The translation term in the affine map $ \zF$ in the definition of NET map presentation does not affect $ \zs_f$. For example, it turns out that changing the translation term in a NET map presentation for $ f(z)=z^2+i$ obtains a NET map $ g$ whose dynamic portrait is different from that of $ f$, but $ \zs_f=\zs_g$. Thus typically, a given NET map $ f$ has three cousins sharing the same induced map $ \zs_f$.
However, there exist other examples: the NET maps with virtual presentation 41HClass19 have the same pullback maps as those with virtual presentation 41HClass24. These phenomena suggest that non-dynamical, Hurwitz-type invariants might be viewed as more fundamental than dynamic portraits.
- (7) It is possible for a NET map $ f$ to have a constant pullback map $ \zs_f$. Examples are given in Cannon et al. ([Cannon et al.2012], [U+00A7]10) and Saenz Maldonado ([Saenz Maldonado2012], Chap. 5). The property that $ \zs_f$ is constant depends only on the impure Hurwitz class of $ f$ and hence only on its Hurwitz structure set (Sect. 4, Hurwitz invariants).

Proposition 5.1 of [Buff et al.2009] provides a way to construct Thurston maps $ f$ with constant pullback maps. Very briefly, the idea here is that if $ f=g\circ s$ and the pullback map of $ s$ maps to a trivial Teichmüller space, then the pullback map of $ f$ is constant. We refer to the hypotheses of this Proposition 5.1 as McMullen's condition.
To describe the NET maps which satisfy McMullen's condition, we define two types of Hurwitz structure sets. Let $ G$ be a finite Abelian group generated by two elements such that $ G/2G\cong (\Z/2\Z)\oplus (\Z/2\Z)$. Let $ \HS$ be a Hurwitz structure set in $ G$. We say that $ \HS$ is an MC2 Hurwitz structure set if $ \HS=\{\pm a\}\amalg \{\pm b\}\amalg \{\pm c\}\amalg \{\pm d\}$, where both $ a$ and $ b$ have order 4 and $ 2a=2b=c-d$. We say that $ \HS$ is an MC4 Hurwitz structure set if $ \HS=\{\pm a\}\amalg \{\pm b\}\amalg \{\pm c\}\amalg \{\pm d\}$, where both $ a$ and $ b$ have order 4, $ 2a\ne 2b$, $ c=a+b$ and $ d=a-b$.
The following theorem essentially answers the question of what NET maps satisfy McMullen's condition. Its proof will appear elsewhere.
Theorem 6.
A NET map is impurely Hurwitz equivalent to a NET map which satisfies McMullen's condition if and only if its Hurwitz structure set is either an MC2 or MC4 Hurwitz structure set.Now that we essentially know what NET maps satisfy McMullen's conditions, what NET maps have constant pullback maps? We do not know the answer, but we have the following. We say that a NET map $ f$ is imprimitive if there exist NET maps $ f_1$ and $ f_2$ such that $ f_1$ is Euclidean, $ f=f_1\circ f_2$ and the postcritical sets of $ f$, $ f_1$ and $ f_2$ are equal. In this case the pullback map of $ f$ is constant if and only if the pullback map of $ f_2$ is constant. We say that $ f$ is primitive if it is not imprimitive. These notions extend to Hurwitz structure sets. We have found five equivalence classes of primitive Hurwitz structure sets whose NET maps have constant pullback maps but which do not satisfy McMullen's condition. Here are representatives for them. \begin{equation*} \{\pm (1,0),\pm (1,1),\pm (7,1),\pm (3,2)\}\subseteq (\Z/8\Z)\oplus (\Z/4\Z)\quad \deg(f)=8 \end{equation*} \begin{equation*} \{\pm (2,0),\pm (0,2),\pm (2,2),\pm (4,2)\}\subseteq (\Z/6\Z)\oplus (\Z/6\Z)\quad \deg(f)=9 \end{equation*} \begin{equation*} \{\pm (1,0),\pm (0,1),\pm (5,1),\pm (2,2)\}\subseteq (\Z/6\Z)\oplus (\Z/6\Z)\quad \deg(f)=9 \end{equation*} \begin{equation*} \{\pm (1,0),\pm (0,1),\pm (1,2),\pm (4,1)\}\subseteq (\Z/6\Z)\oplus (\Z/6\Z)\quad \deg(f)=9 \end{equation*} \begin{equation*} \{\pm (1,0),\pm (1,2),\pm (11,2),\pm (3,3)\}\subseteq (\Z/12\Z)\oplus (\Z/6\Z)\quad \deg(f)=18 \end{equation*}
The second of these is the degree 9 example in Cannon et al. ([Cannon et al.2012], [U+00A7]10) and Saenz Maldonado ([Saenz Maldonado2012], Chap. 5). This leads us to make the following conjecture.
Conjecture 2.
The Hurwitz structure set of every primitive NET map with constant pullback map is either an MC2 or MC4 Hurwitz structure set or it is equivalent to one of the above five exceptional Hurwitz structure sets.This conjecture has been verified by computer for all NET maps with first elementary divisor $ m\le 300$. In particular, it has been verifed for all NET maps with degree at most 300.
- (8) Table 1 gives the possibilities for the genus and number of cusps of $ \mathcal{W}$ for all NET maps with degree at most 8. See Sect. 4 for a discussion of the relationship between $ \cW$, classical modular curves, and Teichmüller curves. Using the Riemann–Hurwitz formula, one can show that \begin{eqnarray*} \deg(Y)=2(g-1)+n. \end{eqnarray*} Note the entries $ (0,3)$ for which $ Y: \mathcal{W} \to \Moduli(S^2, P(f))$ is an isomorphism. The one in degree 4 arises from flexible Lattès maps. The one in degree 8 arises from compositions $ g_2 \circ g_1$, where $ g_1$ is a quadratic Thurston map with three postcritical points and $ g_2$ is a flexible Lattès map; note that every mapping class element lifts under $ g_2$.
- (9) There are many examples of NET maps $ f$ for which $ \sigma_f$ is nonconstant and for which the impure Hurwitz class is completely unobstructed: 22HClass1, 4–6; 31HClass7. Indeed, the impure Hurwitz class of almost every NET map which is a push of a flexible Lattès map is completely unobstructed, and the associated pullback maps are nonconstant. The NET map with presentation diagram in Fig. 5 is an example of this. However, all NET maps whose pullback maps are nonconstant and for which the impure Hurwitz class is completely unobstructed seem to have degrees of the form $ n^2$, $ 2n^2$, $ 3n^2$ or $ 6n^2$. We have verified this by computer through degree 100.
- (10) Among quadratic pure Hurwitz classes, we observe that being completely unobstructed is equivalent to the condition that the inverse $ Y \circ X^{-1}$ of the correspondence extends to a postcritically finite hyperbolic rational map $ g_f: \IP^1 \to \IP^1$ whose postcritical set consists of the three points at infinity in $ \Moduli(S^2, P(f)$.
| $ d$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $ (g,n)$ | (0,4) | (0,6) | (0,3) | (1,6) | (0,6) | (2,6) | (0,3) |
| (0,4) | (1,12) | (0,10) | (4,18) | (0,4) | |||
| (0,6) | (1,8) | (0,6) | |||||
| (0,10) | (1,16) | (0,10) | |||||
| (1,8) | |||||||
| (1,16) | |||||||
| (2,14) | |||||||
| (5,24) |
3. NET Map Presentations

We next describe NET map presentations. This section expands on the discussion of a NET map presentation for the rabbit in the introduction. Details can be found in [Floyd et al.2017a]. We begin with the lattice $ \zL_2=\mathbb{Z}^2$, a proper sublattice $ \zL_1$ and an orientation-preserving affine isomorphism $ \zF\co \mathbb{R}^2\to \mathbb{R}^2$ such that $ \zF(\zL_2)=\zL_1$. Let $ \zG_1$ be the group of isometries of $ \mathbb{R}^2$ of the form $ x\mapsto 2\zl\pm x$ for some $ \zl\in \zL_1$. This information determines a Euclidean Thurston map $ g\co \mathbb{R}^2/\zG_1\to \mathbb{R}^2/\zG_1$ as in the introduction's discussion of a NET map presentation for the rabbit. The postcritical set $ P_1$ of $ g$ is the image of $ \zL_1$ in $ \mathbb{R}^2/\zG_1$. The image of $ \zL_2-\zL_1$ in $ \mathbb{R}^2/\zG_1$ is the set of critical points of $ g$. To describe $ g$, all we need is to express $ \zF$ as $ \zF(x)=Ax+b$, where $ A$ is a $ 2\times 2$ matrix of integers and $ b$ is an integral linear combination of the columns, $ \zl_1$ and $ \zl_2$, of $ A$. We may even assume that $ b$ is either 0, $ \zl_1$, $ \zl_2$ or $ \zl_1+\zl_2$. Then $ \zl_1$, $ \zl_2$ and $ b$ determine $ g$ up to Thurston equivalence.
The parallelogram $ F_1$ with corners 0, $ 2\zl_1$, $ \zl_2$ and $ 2\zl_1+\zl_2$ is a fundamental domain for the action of $ \zG_1$ on $ \mathbb{R}^2$. The points of $ \zL_1$ in $ F_1$ are 0, $ \zl_1$, $ 2\zl_1$, $ \zl_2$, $ \zl_1+\zl_2$ and $ 2\zl_1+\zl_2$. These six points map onto $ P_1$. We choose six line segments (possibly trivial, just a point) whose union is the full inverse image in $ F_1$ of four disjoint arcs $ \zb_1$, $ \zb_2$, $ \zb_3$, $ \zb_4$ in $ \R^2/\zG_1$. Each of the six line segments joins one of 0, $ \zl_1$, $ 2\zl_1$, $ \zl_2$, $ \zl_1+\zl_2$, $ 2\zl_1+\zl_2$ and an element of $ \Z^2$. We call them the point-push line segments , and we call $ \zb_1$, $ \zb_2$, $ \zb_3$, $ \zb_4$ the point-push arcs ; we color them green (dashed) whenever possible.
Recall that if $ \zb$ is an oriented arc in a surface, then a point-pushing homeomorphism along $ \zb$ is a homeomorphism which is the terminal homeomorphism of an isotopy of the surface supported in a regular neighborhood of $ \zb$ that pushes the starting point of $ \zb$ to its ending point along $ \zb$. We have four point-push arcs $ \zb_1$, $ \zb_2$, $ \zb_3$, $ \zb_4$. Pushing along each $ \zb_i$ determines, up to homotopy rel $ P_1$, a "push map" homeomorphism $ h\co \mathbb{R}^2/\zG_1\to \mathbb{R}^2/\zG_1$ which pushes along $ \zb_1$, $ \zb_2$, $ \zb_3$, $ \zb_4$ in $ \mathbb{R}^2/\zG_1$ from $ P_1$ to a set $ P_2$ of four points in the image of $ \zL_2$.
Now that we have $ g$ and $ h$, we set $ f=h\circ g$. This is a Thurston map. It is a NET map if it has four postcritical points, in which case its postcritical set is $ P_2$. This fails only in special situations when the degree of $ f$ is either 2 or 4. (See the second paragraph of Section 2 of [Cannon et al.2012] for more on this.) Every NET map can be expressed as a composition of a Euclidean map and a push map in this way. We call this a NET map presentation of $ f$. The result of omitting the translation term $ b$ from a NET map presentation is by definition a virtual NET map presentation . The program NETmap takes as input a virtual NET map presentation.
So every NET map can be described up to Thurston equivalence by a simple diagram. This diagram consists of first the parallelogram $ F_1$. This determines $ \zl_1$ and $ \zl_2$ and therefore the matrix $ A$. Second, one of the elements 0, $ \zl_1$, $ \zl_2$, $ \zl_1+\zl_2$ in $ F_1$ is circled to indicate the translation term $ b$. Third, the (nontrivial) point-push line segments are drawn in $ F_1$. We call this a NET map presentation diagram. Figure 2 is such a diagram for the rabbit.
Note that the group $ \text{SL}(2,\Z)$ acts naturally on NET map presentation diagrams: given $ P \in \text{SL}(2,\Z)$, transform the entire diagram by application of $ P$. In [Floyd et al.2017a] it is shown that this corresponds to postcomposition by the element of the modular group determined by $ P$.
4. Hurwitz Classes

Hurwitz Equivalence. Let $ f,f'\co S^2\to S^2$ be Thurston maps with postcritical sets $ P =P(f)$ and $ P'=P(f')$. We say that $ f$ and $ f'$ belong to the same modular group Hurwitz class if there exist orientation-preserving homeomorphisms $ h_0,h_1\co (S^2,P)\to (S^2,P')$ such that $ h_0\circ f=f'\circ h_1$. If in addition $ h_0$ and $ h_1$ agree on $ P$, then we say that $ f$ and $ f'$ belong to the same pure modular group Hurwitz class. For brevity, we usually speak of pure and impure Hurwitz classes.
Proof of Theorem 5. Statements 1 and 2 of Theorem 3 imply that there is an algorithm which computes $ c_f(p/q)$ and $ d_f(p/q)$ for every slope $ p/q$. Theorem 4.1 of [Cannon et al.2012] implies that these values depend only on the image of the ordered pair $ (q,p)$ in $ \mathbb{Z}_{2m}\oplus \mathbb{Z}_{2n}$ once $ \zL_2/2\zL_1$ is appropriately identified with $ \mathbb{Z}_{2m}\oplus \mathbb{Z}_{2n}$. This proves that there is an algorithm which computes the image of $ \zd_f$.
Let $ h\co (S^2,P(f))\to (S^2,P(f))$ be an orientation-preserving homeomorphism. Then $ h$ induces by pullback a bijection $ \zm_h$ on slopes. Let $ s$ be a slope. Then $ c_{h\circ f}(s)=c_f(\zm_h(s))$ and $ d_{h\circ f}(s)=d_f(\zm_h(s))$. Also, $ c_{f\circ h}(s)=c_f(s)$ and $ d_{f\circ h}(s)=d_f(s)$. This proves the second assertion of Theorem 5.
We now establish the three final assertions. Statement 1 follows from Koch et al. ([Koch et al.2016], Theorem 5.1). Statement 2 follows from W. Thurston's characterization theorem and the observation that the impure modular group acts transitively on slopes.
We now turn to the necessity in statement 3. Let $ \simeq$ denote the equivalence relation on $ \HHH$ determined by isotopy rel $ P=P(f)$. So $ \HHH/\!\!\simeq$ is the set of isotopy classes of maps in the impure Hurwitz class of $ f$; in what follows, we write equality for equality in this set.
The full modular group $ \Mod(S^2, P)$ acts on $ \HHH/\!\!\simeq$ both by pre-composition and post-composition. The set of combinatorial classes in $ \HHH$ is in bijective correspondence with the orbits of the induced conjugation action of $ \Mod(S^2, P)$ on $ \HHH/\!\!\simeq$. Since the pure mapping class group $ \PMod(S^2, P)$ has finite index in $ \Mod(S^2, P)$, it suffices to show that there are infinitely many orbits under the conjugation action of $ \PMod(S^2, P)$.
The assumption $ 1 \in \delta_f(\HHH)$ implies that there exist $ h_0, h_1$ representing elements of $ \Mod(S^2, P)$ for which $ f_*:=h_0fh_1$ has an obstruction given by a curve $ \gamma$ with multiplier equal to $ 1$. Let $ T$ be a (full, not half) Dehn twist about $ \gamma$. By Koch et al. ([Koch et al.2016], Theorem 9.1) there is a smallest positive integer $ k$ such that $ T^k$ commutes with $ f_*$ up to isotopy relative to $ T^kf_*=f_*T^k$ in $ \HHH/\!\!\simeq$. Let $ k'$ be the smallest positive integer for which $ T^{k'}$ lifts under $ f_*$ to an element of $ \Mod(S^2, P)$. Since Dehn twists must lift to Dehn twists, and $ f_*$ leaves $ \gamma$ invariant, we have $ T^{k'}f_*=f_*T^{k''}$ for some $ k'' \in \mathbb{Z}$. Since $ k'$ is minimal, $ k=nk'$ for some positive integer $ n$. Thus $ f_*T^{nk'}=f_*T^k=T^kf_*=T^{nk'}f_*=f_*T^{nk''}$. The right action of $ \PMod(S^2, P)$ on $ \HHH/\!\!\simeq$ is free ([Pilgrim2012], [U+00A7]3 or [Kameyama2001], Prop. 4.1) and so $ k=k'$.
For $ n \in \mathbb{Z}$ let $ f_n:=f_*T^n$. We claim that for $ n \neq m \in \mathbb{Z}$, the maps $ f_n$ and $ f_m$ are not conjugate via an element of $ \PMod(S^2, P)$. We argue somewhat similarly as in Koch et al. ([Koch et al.2016], [U+00A7]9). Suppose as elements of $ \HHH/\!\!\simeq$ we have $ hf_n=f_mh$ for some $ h \in \PMod(S^2, P)$. The (class of) curve $ \gamma$ is the unique obstruction for both $ f_n$ and $ f_m$, so $ h$ must fix the class of $ \gamma$. Since $ h \in \PMod(S^2, P)$, $ h$ is a power of $ T$, say $ T^l$. Then $ hf_n=f_mh \implies T^lf_*T^n=f_*T^mT^l$. This equation implies that $ T^l$ lifts under $ f_*$ to a pure mapping class element and so by the previous paragraph $ l=qk$ for some $ q$. Continuing, we have $ f_*T^mT^l =T^lf_*T^n= T^{qk}f_*T^n=f_*T^nT^{qk}\implies f_*T^{qk}T^n=f_*T^mT^{qk}\implies f_*T^{n+l}=f_*T^{m+l}\implies n=m$, again by freeness of the right action.
To prove sufficiency, suppose $ 1 \not\in \delta({\mathcal{H}})$. It suffices to show there are only finitely many combinatorial classes of obstructed maps. We use the combination and decomposition theory developed in [Pilgrim2003] and outline the main ideas.
Suppose $ f \in \mathcal{H}$ has an obstruction, $ \gamma$. Let $ A_0$ be an annulus which is a regular neighborhood of $ \gamma$ and put $ \AAA_0:=\{A_0\}$. By altering $ f$ within its homotopy class we may assume that the collection $ \AAA_1$ of preimages of $ A_0$ containing essential nonperipheral preimages of $ \gamma$ is a collection of essential subannuli of $ A_0$ with $ \partial \AAA_1 \supset \partial A_0$; the restriction $ f: \AAA_1 \to \AAA_0$ is the set of annulus maps obtained by decomposing $ f$ along $ \{\gamma\}$. Similarly, if we set $ \UUU_0$ to be the collection of two components of $ S^2-\AAA_0$, we obtain a collection of sphere maps $ f: \UUU_1 \to \UUU_0$. Capping the holes of the sphere maps to disks yields a collection of Thurston maps with three or fewer postcritical points, and these are rational, by Thurston's characterization.
As $ f$ varies within $ \mathcal{H}$, the collection of sphere maps varies over a finite set of combinatorial equivalence classes, since they are rational. The hypothesis that the multiplier of the obstructions are not equal to one implies that the set of combinatorial equivalence classes of annulus maps vary over a finite set as well. The additional set-theoretic gluing data needed to reconstruct $ f$ from the sphere and annulus maps also varies over a finite set. By Pilgrim ([Pilgrim2003], Theorem 4.5), given two maps $ f_1, f_2$ presented as a gluing of sphere and annulus maps, a combinatorial equivalence between gluing data, a collection of annulus maps, and a collection of sphere maps yields a combinatorial equivalence between $ f_1$ and $ f_2$. We conclude that the set of possible equivalence classes of maps $ f$ in $ \mathcal{H}$ is finite.
Modular Groups. From the discussion of the NET map presentation of the rabbit (Sect. 1) and of NET map presentations (Sect. 3), recall the definition of the quotient sphere $ S^2_2:=\R^2/\Gamma_2$. Equipped with its Euclidean half-translation structure, it is a "square pillowcase" with four corners given by the images of the lattice $ \Lambda_2=\Z^2$. Let $ P$ be this set of corners. In this case the modular group $ \text{Mod}(S^2,P)$ and pure modular group $ \text{PMod}(S^2,P)$ have the forms \begin{eqnarray*} \Mod(S^2, P) \cong \PSL(2,\Z)\ltimes (\Z/2\Z\times\Z/2\Z) \end{eqnarray*} and \begin{eqnarray*} \PMod(S^2, P) \cong P\Gamma(2)=\{A \equiv I \bmod 2\} \subseteq \PSL(2,\Z). \end{eqnarray*} The group $ \Mod(S^2, P)$ is then the group of orientation-preserving affine diffeomorphisms, and $ P\Gamma(2)$ the subgroup fixing the corners pointwise. The group $ \PSL(2,\Z)$ fixes the corner corresponding to the image of the origin, but permutes the other three corners so as to induce the natural action of the symmetric group $ S_3$.
Hurwitz Invariants. Useful invariants of a NET map are its elementary divisors , which we now define. Suppose $ f$ is a NET map given by a NET map presentation with affine map $ x \mapsto Ax+b$, where $ A$ is an integral matrix whose determinant equals the degree of $ f$. There are $ P, Q \in \text{SL}(2,\Z)$ and positive integers $ m$ and $ n$ such that $ n|m$ and $ PAQ=\left[\begin{smallmatrix}m & 0 \\ 0 & n \end{smallmatrix}\right]$. The integers $ m,n$ are unique and are the elementary divisors of $ A$; the matrix on the right is the Smith normal form . They form an impure Hurwitz invariant. In fact, according to Floyd et al. ([Floyd et al.2017b], Theorem 5.5), NET maps $ f$ and $ g$ have equal elementary divisors if and only if $ g$ is Thurston equivalent to a NET map of the form $ \zv\circ f$ for some homeomorphism $ \zv\co S^2\to S^2$. (Note that $ \zv$ need not stabilize $ P(f)$.)
For NET maps, a complete invariant of impure Hurwitz classes can be given in terms of the Hurwitz structure set , $ \mathcal{HS}$. To define this, we use the usual data and Euclidean groups associated to a NET map $ f$. The torus $ \mathbb{R}^2/2\zL_1$ is a double cover of the sphere $ \mathbb{R}^2/\zG_1$. The pullback of $ P(f)$ in $ \mathbb{R}^2/2\zL_1$ is a subset of the finite group $ \mathbb{Z}^2/2\zL_1$, and it is a disjoint union of the form $ \HS=\{\pm h_1\}\amalg\{\pm h_2\}\amalg\{\pm h_3\}\amalg\{\pm h_4\}$. This is a Hurwitz structure set. More generally, let $ G$ be a finite Abelian group such that $ G/2G\cong (\Z/2\Z)\oplus (\Z/2\Z)$. A Hurwitz structure set in $ G$ is a disjoint union of four sets of the form $ \{\pm h\}$, where $ h\in G$. Returning to $ \HS$, if $ \zL'_1$ is a sublattice of $ \mathbb{Z}^2$, then we say that $ \HS$ is equivalent to a Hurwitz structure set $ \HS'$ in $ \mathbb{Z}^2/2\zL'_1$ if and only if there exists an orientation-preserving affine isomorphism $ \zJ\co \mathbb{Z}^2\to \mathbb{Z}^2$ such that $ \zJ(\zL_1)=\zL'_1$ and the map which $ \zJ$ induces from $ \mathbb{Z}^2/2\zL_1$ to $ \mathbb{Z}^2/2\zL'_1$ takes $ \HS$ to $ \HS'$. Theorem 5.1 of [Floyd et al.2017b] states that the equivalence class of $ \HS$ under this equivalence relation is a complete invariant of the impure Hurwitz class of $ f$.
Relating $ \cW$ to Classical Modular Curves. Let $ f$ be a NET map with postcritical set $ P(f)$. Recall the correspondence $ X, Y: \cW \to \Moduli(S^2, P(f))$ from Sect. 1. This correspondence is essentially an impure Hurwitz invariant; see Koch ([Koch2013], [U+00A7]2). In this section we explicitly relate the space $ \cW$ to classical modular curves. Corollary 5.3 of [Floyd et al.2017b] states that every impure Hurwitz class of NET maps is represented by a NET map whose presentation matrix is diagonal. So to understand $ \cW$, we may assume that the presentation matrix of $ f$ has the form $ A=\left[\begin{smallmatrix} m& 0 \\ 0 & n\end{smallmatrix}\right]$, where $ m$ and $ n$ are positive integers with $ n|m$ and $ mn=\deg(f)$. By definition, $ m$ and $ n$ are the elementary divisors of $ f$. So the presentation of $ f$ has lattices $ \zL_2=\mathbb{Z}^2$ and $ \zL_1=\langle (m,0),(0,n)\rangle $. It also has a Hurwitz structure set $ \mathcal{HS}\subseteq\zL_2/2\zL_1$. The discussion at the end of [U+00A7]2 of [Floyd et al.2017b] shows that the group $ G_f$ of pure liftables is isomorphic to the image in $ \text{PSL}(2,\mathbb{Z})$ of the group $ \widehat{G}_f$ of all elements $ M$ in $ \text{SL}(2,\mathbb{Z})$ such that $ M \zL_1=\zL_1$, $ M\equiv 1\text{ mod } 2$ and the automorphism of $ \Z^2/2\zL_1$ induced by $ M$ fixes $ \mathcal{HS}$ pointwise up to multiplication by $ \pm 1$.
We interrupt this discussion to define some subgroups of $ \text{SL}(2,\mathbb{Z})$. Let $ N$ be a positive integer. The principle congruence subgroup of $ \text{SL}(2,\mathbb{Z})$ with level $ N$ is \begin{equation*} \zG(N)=\left\{\left[\begin{smallmatrix}a & b \\ c & d \end{smallmatrix}\right]\in \text{SL}(2,\mathbb{Z}):\left[\begin{smallmatrix}a & b \\ c & d \end{smallmatrix}\right]\equiv \left[\begin{smallmatrix}1 & 0 \\ 0 & 1 \end{smallmatrix}\right]\text{ mod } N\right\}. \end{equation*} A congruence subgroup of $ \text{SL}(2,\mathbb{Z})$ is a subgroup which contains $ \zG(N)$ for some $ N$. Two such subgroups are \begin{equation*} \zG_0(N)=\left\{\left[\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right]\in \text{SL}(2,\mathbb{Z}):c \equiv 0 \text{ mod } N\right\} \end{equation*} and \begin{equation*} \zG^0(N)=\left\{\left[\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right]\in \text{SL}(2,\mathbb{Z}):b \equiv 0 \text{ mod } N\right\}. \end{equation*} Two others are \begin{equation*} \zG_1(N)=\left\{\left[\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right]\in \zG_0(N):a \equiv d\equiv 1 \text{ mod } N\right\} \end{equation*} and \begin{equation*} \zG^1(N)=\left\{\left[\begin{smallmatrix}a & b \\ c & d\end{smallmatrix}\right]\in \zG^0(N):a \equiv d\equiv 1 \text{ mod } N\right\}. \end{equation*}
We next relate $ \widehat{G}_f$ to these congruence subgroups. The condition that $ M\equiv 1\text{ mod }2$ simply says that $ \widehat{G}_f\subseteq \zG(2)$. We next interpret the condition that $ M \zL_1=\zL_1$. Let $ M=\left[\begin{smallmatrix} a& b \\ c & d \end{smallmatrix}\right]$. Since $ (0,n)\in \zL_1$, we need that $ M\cdot (0,1)\in \zL_1$. Equivalently, $ (bn,dn)\in \zL_1$. This amounts to requiring that $ bn\equiv 0\text{ mod } m$, that is, $ b\equiv 0\text{ mod }\frac{m}{n}$. Since $ n|m$, the condition that $ M\cdot (m,0)\in \zL_1$ is satisfied by every $ M\in \text{SL}(2,\mathbb{Z})$. Hence the condition that $ M \zL_1=\zL_1$ is equivalent to the condition that $ M\in \zG^0(\frac{m}{n})$. Therefore $ \widehat{G}_f\subseteq \zG^0(\frac{m}{n})\cap \zG(2)$. On the other hand, the group $ \zG^1(2m)\cap \zG_1(2n)$ stabilizes $ \zL_1$ and acts trivially on $ \zL_2/2\zL_1$, and so it fixes $ \mathcal{HS}$ pointwise. Thus \begin{equation*} \zG(2m)\subseteq \zG^1(2m)\cap \zG_1(2n)\subseteq \widehat{G}_f\subseteq \zG^0(\tfrac{m}{n})\cap \zG(2). \end{equation*}
In conclusion, let $ \mathbb{H}^*$ be the Weil-Petersson completion of $ \mathbb{H}$. Then $ \cW$ is a modular curve such that $ \mathbb{H}^*/(\zG^1(2m)\cap \zG_1(2n))$ maps onto $ \cW$ and $ \cW$ maps onto $ \mathbb{H}^*/(\zG^0(\frac{m}{n})\cap \zG(2))$.
5. Invariants of Degree 2 NET
Maps

We begin with a discussion of invariants of general Thurston maps and then specialize to NET maps with degree 2.
The dynamic portrait is the directed graph with vertex set $ C(f) \cup P(f)$ and weighted edges \begin{eqnarray*} x {\xrightarrow{\deg_x(f)}} f(x). \end{eqnarray*} The static portrait is the bipartite directed graph whose vertex set is the disjoint union of $ A:=C(f) \cup P(f)$ and $ B:=P(f)$, directed edges \begin{eqnarray*} x {\xrightarrow{\deg_x(f)}}f(x) \end{eqnarray*} with $ x\in A$, and the elements of $ A$ that lie in $ P(f)$ are marked so as to distinguish them from those elements of $ A$ that do not lie in $ P(f)$. The augmented branch data records, for each $ y \in P(f)$, the partition of $ d=\deg(f)$ given by the collection of local degrees $ \{\deg_x(f) : f(x)=y\}$. For example, the dynamic portrait of the rabbit is $ (a \two b \to c \to a, d\two d)$, the static portrait is $ (p_1 \two q_1, p_2 \two q_2, p_3 \to q_3, p_4\to q_4)$, and the branch data is $ ([2],[2],[1,1],[1,1])$. The static portrait, and hence branch data, are impure Hurwitz invariants. The dynamic portrait is a pure Hurwitz invariant but not, in general, an impure Hurwitz invariant.
For NET maps, dynamic and static portraits are completely classified [Floyd et al.2017b]. Table 2 gives the number of dynamic portraits as a function of the degree.
| $ d$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| $ n$ | 16 | 94 | 272 | 144 | 338 | 152 | 476 |
| $ d\mod 4, d\ge9$ | 0 | 1 | 2 | 3 | |||
| $ n$ | 483 | 153 | 353 | 153 |
Degree 2 NET Maps. Recall that a quadratic Thurston map is NET if and only if it has four postcritical points. In degree 2 there are 3 impure Hurwitz classes, completely classified by static portrait or, equivalently, by the number of critical points in the postcritical set; see Theorem 7. Here are the three static portraits. We label marked points in the domain by $ p_i$, we label marked points in the codomain by $ q_i$, and we label unmarked critical points in the domain by $ c_i$. \begin{eqnarray*} \begin{array}{l} p_1\to q_1, p_2\to q_1, p_3\to q_2, p_4\to q_2, c_1\two q_3, c_2\two q_4\\ p_1 \to q_1, p_2 \to q_1, p_3 \two q_2, p_4 \to q_3, c_1 \two q_4\\ p_1 \two q_1, p_2 \two q_2, p_3\to q_3, p_4\to q_4 \end{array} \end{eqnarray*} Pure Hurwitz classes are completely classified by the corresponding dynamic portraits. There are 16 of them. All but one is represented by rational functions; the exception is $ a \two b \to a$, $ c\two d \to c$. [Kelsey and Lodge2017] have completed the classification of quadratic NET combinatorial classes. They generalize the methods of Bartholdi–Nekrashevych on the twisted rabbit problem ([Bartholdi and Nekrashevych2006]), analyzing wreath recursions on the pure mapping class group. These wreath recursions are derived from the 16 correspondences on moduli space.
Impure Hurwitz classes in degree 2. In this section we prove Theorem 7. It shows that two NET maps with degree 2 belong to the same impure Hurwitz class if and only if they have the same number of critical postcritical points. These maps all have two critical points and four postcritical points. So there might be either 0, 1 or 2 critical postcritical points. Hence there are three impure Hurwitz classes of NET maps with degree 2. The case in which there are no critical postcritical points is exactly the case of the Euclidean NET maps with degree 2. They form one impure Hurwitz class. Another is represented by $ f(z)=z^2+i$ and the other is represented by the rabbit, corabbit and airplane. Here is the theorem.
Theorem 7.
Two degree 2 NET maps belong to the same impure Hurwitz class if and only if they have the same number of critical postcritical points.Proof.
Let $ f$ be a degree 2 NET map. The elementary divisors of $ f$ are $ m=2$ and $ n=1$ because their product is $ \deg(f)=2$ and the second divides the first. The group $ \Lambda_2/2\Lambda_1$ in the definition of Hurwitz structure set is then isomorphic to $ \Z_4 \oplus \Z_2$. The Hurwitz structure set $ \mathcal{HS}$ of $ f$ can thus be identified with a subset of \begin{equation*} \mathbb{Z}_4\oplus \mathbb{Z}_2 =\{(0,0),\pm (1,0),(2,0),(0,1), \pm (1,1),(2,1)\}. \end{equation*} Elements of order 1 or 2 in $ \mathcal{HS}$ correspond to postcritical points of $ f$ which are not critical. The other elements of $ \mathcal{HS}$ are paired by multiplication by $ -1$, and these pairs correspond to critical postcritical points. It is shown in [Floyd et al.2017b] that two NET maps with equal Hurwitz structure sets belong to the same impure Hurwitz class. Moreover, transforming $ \mathcal{HS}$ either by an automorphism of $ \mathbb{Z}_4\oplus \mathbb{Z}_2$ which lifts to $ \text{SL}(2,\mathbb{Z})$ or by a translation by an element of order 2 preserves the impure Hurwitz class of $ f$.It is easy to see that if two NET maps belong to the same impure Hurwitz class, then they have the same number of critical postcritical points. The converse statement is what must be proved.
Suppose that $ f$ is a NET map with degree 2 and no critical postcritical points. Then the first paragraph of this proof shows that there is only one possibility for the Hurwitz structure set of $ f$ after identifying it with a subset of $ \mathbb{Z}_4\oplus \mathbb{Z}_2$; it must be $ \{(0,0),(2,0),(0,1),(2,1)\}$. So there is just one impure Hurwitz class of such maps.
Next suppose that $ f$ is a NET map with degree 2 and exactly one critical postcritical point. Then the Hurwitz structure set of $ f$ contains three of the four elements of order 1 or 2 in $ \mathbb{Z}_4\oplus \mathbb{Z}_2$. Since translation by an element of order 2 preserves the impure Hurwitz class of $ f$, we may assume that $ \mathcal{H}$ contains $ (0,0)$, $ (2,0)$, $ (0,1)$ and either $ \pm (1,0)$ or $ \pm (1,1)$. Now we verify that $ \left[\begin{smallmatrix}1 & 0 \\ 1 & 1 \end{smallmatrix}\right]\in \text{SL}(2,\mathbb{Z})$ induces an automorphism of $ \mathbb{Z}_4\oplus \mathbb{Z}_2$ which fixes $ (0,0)$, $ (2,0)$, $ (0,1)$ and interchanges $ \pm (1,0)$ and $ \pm (1,1)$. Thus there is only one equivalence class of these Hurwitz structure sets and only one impure Hurwitz class of such maps.
Finally, suppose that $ f$ is a NET map with degree 2 and two critical postcritical points. In this case $ \mathcal{HS}$ must contain $ \pm (1,0)$ and $ \pm (1,1)$ in addition to two of the four elements of order 1 or 2. Since translating $ \mathcal{HS}$ by an element of order 2 preserves the impure Hurwitz class of $ f$, we may assume that $ \mathcal{HS}$ contains $ \pm (1,0)$, $ \pm (1,1)$ and $ (0,0)$.
Suppose in addition that $ (2,0)\in \mathcal{HS}$. Then $ \mathcal{HS}=\{(0,0),\pm (1,0),(2,0),\pm 1,1)\}$. Example 10.3 of [Cannon et al.2012] shows that $ \mathcal{HS}$ is never separating (nonseparating in the language there). Between Lemma 10.1 and Theorem 10.2 of [Cannon et al.2012] it is shown that this implies that the Thurston pullback map of $ f$ is constant. But Theorem 10.10 of [Cannon et al.2012] shows that there does not exist a NET map with degree 2 whose Thurston pullback map is constant. (The Thurston maps for this choice of $ \mathcal{HS}$ have fewer than four postcritical points.) Thus $ (2,0)\notin \mathcal{HS}$.
So $ \mathcal{HS}$ contains either $ (0,1)$ or $ (2,1)$. One verifies that $ \left[\begin{smallmatrix}1 & 2 \\ 0 & 1 \end{smallmatrix}\right]\in \text{SL}(2,\mathbb{Z})$ induces an automorphism on $ \mathbb{Z}_4\oplus \mathbb{Z}_2$ which fixes $ (0,0)$, $ \pm (1,0)$, $ \pm (1,1)$ and interchanges $ (0,1)$ and $ (2,1)$. Hence there is only one equivalence class of these Hurwitz structure sets and only one impure Hurwitz class of such maps.
This proves Theorem 7. ⬜
6. A Conformal Description of
$ \zs_f$ for a Degree 2 Example

In this section we discuss how in many, but not all, cases it is possible in a sense to determine the pullback map $ \zs_f\co \mathbb{H}\to \mathbb{H}$ of a NET map $ f$. This description is like that of the classical triangle functions, as discussed in Chapter 1 of [Lehner1964]. For the triangle functions, we begin with a conformal equivalence between a hyperbolic triangle and the upper half plane. Here we begin with a conformal equivalence between two hyperbolic triangles or, more generally, two hyperbolic polygons. The map is then extended to the entire hyperbolic plane using the reflection principle.
We will focus on a particular example map $ f_0$. Our discussion involves several features of $ f_0$. For each feature, we provide first a brief general discussion for arbitary NET maps $ f$, and then illustrate it using our example map $ f_0$.
Example.
The NET map $ f_0$. Our example map $ f_0$ is determined up to Thurston equivalence by the presentation diagram in Fig. 8. We have lattices $ \zL_2=\mathbb{Z}^2$, $ \zL_1=\langle (2,0),(0,1)\rangle $ and Hurwitz structure set \begin{equation*} \mathcal{HS}=\{(0,0),\pm (1,0),(2,0),(0,1)\}\subseteq \mathbb{Z}_4\oplus \mathbb{Z}_2\cong \zL_2/2\zL_1. \end{equation*} We also have a Euclidean NET map $ g$ and a push map $ h$ such that $ f_0=h\circ g$.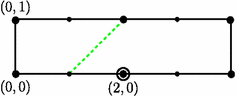
The subgroup $ G_f$ of liftables in the extended modular group $ G$. Suppose $ f$ now is an arbitrary NET map. We work with the extended modular group $ G=\text{EMod}(S^2,P(f))$, which is defined in the same way as the modular group $ \text{Mod}(S^2,P(f))$ except that it allows reversal of orientation. [U+00A7]2 of [Floyd et al.2017b] shows that $ G$ is isomorphic to the group $ \text{Aff}(2,\mathbb{Z})$ of all affine isomorphisms $ \zJ\co \mathbb{R}^2\to \mathbb{R}^2$ such that $ \zJ(\mathbb{Z}^2)=\mathbb{Z}^2$ modulo the subgroup $ \zG_2$ of all maps of the form $ x\mapsto 2\zl\pm x$ for some $ \zl\in \zL_2=\mathbb{Z}^2$.
A map $ \zv\co (S^2,P(f))\to (S^2,P(f))$ representing a homotopy class in $ G$ is liftable if there exists another such map $ \widetilde{\zv}$ such that $ \zv\circ f$ is homotopic to $ f\circ \widetilde{\zv}$ rel $ P(f)$. The subgroup of liftables for $ f$ is the subgroup $ G_f$ of $ G$ represented by all such liftable maps $ \zv$. [U+00A7]2 of [Floyd et al.2017b] shows that $ G_f$ is isomorphic to the subgroup of $ G$ whose elements lift to elements $ \zJ\in \text{Aff}(2,\mathbb{Z})$ such that $ \zJ(\zL_1)=\zL_1$ and the map induced by $ \zJ$ on $ \zL_2/2\zL_1$ stabilizes $ \mathcal{HS}$ setwise. Turning to our example map $ f_0$, we let \begin{equation*} \zJ_1(x)=\left[\begin{smallmatrix}1 & 0 \\ 0 & -1 \end{smallmatrix}\right]x, \quad \zJ_2(x)=\left[\begin{smallmatrix}-1 & 0 \\ 2 & 1 \end{smallmatrix}\right]x, \quad \zJ_3(x)=\left[\begin{smallmatrix}1 & 2 \\ 0 & -1 \end{smallmatrix}\right]x. \end{equation*} These are elements of $ \text{Aff}(2,\mathbb{Z})$ which stabilize $ \zL_1$ and $ \mathcal{HS}$. So $ \zJ_1$, $ \zJ_2$ and $ \zJ_3$ determine elements $ \zr_1$, $ \zr_2$ and $ \zr_3$ of $ G_{f_0}$.
In this paragraph we show that $ \zr_1$, $ \zr_2$ and $ \zr_3$ generate $ G_{f_0}$. Let $ G_{f_0}^+$ denote the subgroup of orientation-preserving elements of $ G_{f_0}$. The discussion in Sect. 4 which relates $ \cW$ to classical modular curves shows that if $ \zJ(x)=Ax+b\in \text{Aff}(2,\mathbb{Z})$ is the lift of an element of $ G_{f_0}^+$, then $ A\in \zG^0(2)$. Moreover, one easily verifies that there is no such $ \zJ$ with $ A=\left[\begin{smallmatrix}1 & 0 \\ 1 & 1 \end{smallmatrix}\right]$, an element of $ \zG^0(2)$. So the set of these matrices arising as lifts of elements of $ G_{f_0}^+$ is a proper subgroup of $ \zG^0(2)$. On the other hand, we will soon see from Fig. 10 that the images of $ \zr_1$, $ \zr_2$ and $ \zr_3$ in $ \text{PGL}(2,\mathbb{Z})$ generate a subgroup with index 6. (Its intersection with $ \text{PSL}(2,\mathbb{Z})$ equals the image of $ \zG(2)$.) It easily follows that $ G_{f_0}$ is generated by $ \zr_1$, $ \zr_2$, $ \zr_3$ together with the elements of $ G_{f_0}$ which lift to translations in $ \text{Aff}(2,\mathbb{Z})$. One finally verifies that only the identity element of $ G_{f_0}$ lifts to a translation. Therefore $ \zr_1$, $ \zr_2$ and $ \zr_3$ generate $ G_{f_0}$.
Evaluation of $ \zm_f$. Let $ \zm_{f_0}$ denote the usual slope function which $ f_0$ induces on slopes of simple closed curves in $ S^2-P(f_0)$. We want to evaluate $ \zm_{f_0}$ at $ -1$, $ -\frac{1}{2}$, 1 and $ \infty$. This can be done using Theorem 5.1 of [Cannon et al.2012], which provides a method suitable for computer implementation. In the next paragraph we evaluate $ \zm_{f_0}(-\frac{1}{2})$ in a more topological way. The other three evaluations can be made similarly.
The left side of Fig. 9 shows the pullback to the diagram in Fig. 8 of a simple closed curve $ \zg$ in $ S^2-P(f_0)$ with slope $ -\frac{1}{2}$; it is straightforward to check this by taking the image of the curves under $ f_0$. The right side of Fig. 9, while actually meaningless, might be helpful. We see that $ f_0^{-1}(\zg)$ has two connected components, one drawn with dots and the other drawn with dashes. The dotted connected component is peripheral. On the other hand, the image in $ S^2$ of the line segment joining $ (0,0)$ and $ (1,0)$ is a core arc for the other connected component. Recall that $ f=h\circ g$ where $ g$ is Euclidean and $ h$ is a push map. The slope of this core arc relative to $ P(f_0)$ equals the slope of its image under $ h^{-1}$ relative to $ P(g)$. This image under $ h^{-1}$ is homotopic rel $ P(g)$ to the line segment joining $ (0,0)$ and $ (2,1)=1\cdot (2,0)+1\cdot (0,1)$. Hence $ \zm_{f_0}(-\frac{1}{2})=\frac{1}{1}=1$. In the same way, we find that $ \zm_{f_0}(-1)=0$, $ \zm_f(1)=2$ and $ \zm_{f_0}(\infty)=\infty$.
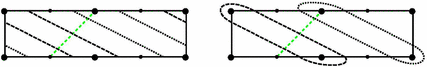
Evaluation of $ \zm_\zv$. We continue with some generalities on affine maps. For an extended modular group element $ \zv\in G$ let $ \zm_\zv$ denote the induced map on slopes. Suppose that $ \zv$ lifts to $ \zF\in \text{Aff}(2,\mathbb{Z})$ with linear part given by the matrix $ A=\left[\begin{smallmatrix}a & b \\ c & d \end{smallmatrix}\right]$. Then $ A^{-1}$ maps the line through $ (0,0)$ and $ (q,p)$ to the line through $ (0,0)$ and \begin{equation*} \left[\begin{smallmatrix}d & -b \\ -c & a \end{smallmatrix}\right]\cdot (q,p)=(-bp+dq,ap-cq). \end{equation*} So $ \zm_\zv(s)=\frac{as-c}{-bs+d}$, where $ s=\frac{p}{q}$.
Evaluation of $ \zs_\zv$. Still focusing on generalities, let $ \zs_\zv$ denote the map on $ \mathbb{H}$ induced by an extended modular group element $ \zv\in G$. To determine $ \zs_\zv$, it suffices to determine the action of $ \zs_\zv$ on $ \partial \mathbb{H}$. We use the expression for $ \zm_\zv$ in the previous paragraph. Because the slope $ s$ corresponds to $ x=-\frac{1}{s}\in \partial \mathbb{H}$, the map which $ \zv$ induces on $ \partial \mathbb{H}$ is \begin{equation*} \zs_\zv(x)=-\left(\frac{a(-1/x)-c}{-b(-1/x)+d}\right)^{-1}= \frac{dx+b}{cx+a}. \end{equation*}
So if $ z\in \mathbb{H}$, then \begin{equation*} \zs_\zv(z)=\frac{dz+b}{cz+a}\quad\text{ if }\quad \zv\in G^+\quad \text{ and }\quad \quad\zs_\zv(z)=\frac{d \overline{z}+b}{c \overline{z}+a} \quad\text{ if }\quad \zv\notin G^+. \end{equation*}
The map $ f_0$ induces a virtual endomorphism $ \phi_{f_0}: G \dashrightarrow G$. For a general NET map $ f$, given an extended modular group element $ g \in G$, a lift of $ g$ under $ f$ might not be unique. Thus lifting under $ f$ maps liftable elements to cosets of $ \text{DeckMod}(f)$, the subgroup of $ G$ represented by deck transformations of $ f$. Proposition 2.4 of [Floyd et al.2017b] implies that $ \text{DeckMod}(f)$ is isomorphic to the group of translations in $ 2\zL_2$ which stabilize the Hurwitz structure set $ \mathcal{HS}$ modulo the group of translations in $ 2\zL_1$. For our example $ f_0$, this quotient group is trivial; we obtain a well-defined virtual endomorphism $ \phi_{f_0}: G \dashrightarrow G$ induced by $ f_0$.
The extended modular group virtual endomorphism maps reflections to reflections. A NET map $ f$ preserves orientation. Therefore, if $ g \in G$ reverses orientation and $ \tilde{g}$ is any lift of $ g$ under $ f$, then $ \tilde{g}$ must reverse orientation.
For our example map $ f_0$, since $ \phi_{f_0}$ is a homomorphism, if $ g \in G$ is a reflection, then $ g$ has order two, therefore $ \phi_{f_0}(g)$ both has order $ 2$ and reverses orientation, and is therefore again a reflection. Thus in terms of the action of liftable extended mapping class elements $ G_{f_0}$ on $ \mathbb{H}$, reflections map to reflections under $ \phi_{f_0}$.
Evaluation of the extended modular group virtual endomorphism. We continue to focus on our example map $ f_0$. If $ \zv\in G_{f_0}$, then we let $ \widetilde{\zv}=\phi_{f_0}(\zv)$. In this paragraph we evaluate $ \zm_{\zr_i}$, $ \zs_{\zr_i}$, $ \zm_{\widetilde{\zr}_i}$ and $ \zs_{\widetilde{\zr}_i}$ for $ i\in \{1,2,3\}$. Using the formulas for $ \zm_{\zr_1}$ and $ \zs_{\zr_1}$ above, we obtain the leftmost two equations in line 6.1. We next apply the identity $ \zm_f\circ \zm_\zv=\zm_{\widetilde{\zv}}\circ \zm_{f_0}$ for $ \zv\in G_{f_0}$. Combining this with $ \zm_{\zr_1}$ and our values for $ \zm_{f_0}$, we obtain the commutative diagram in line 6.1. Using the bottom map of the commutative diagram and the fact that the extended modular group virtual endomorphism maps reflections to reflections, we easily obtain the rightmost two equations in line 6.1. We verify the information in lines 6.2 and 6.3 similarly.
| \begin{equation}\label{lin:rhoone} \require{AMScd} {\begin{aligned} \zm_{\zr_1}(s)&= -s\\ \zs_{\zr_1}(z)&= -z \end{aligned} \qquad \begin{CD} \infty,-1 @> \zm_{\zr_1}> > \infty,1\\ @V\zm_{f_0}VV @VV\zm_{f_0}V\\ \infty,0 @> \zm_{\widetilde{\zr}_1}> > \infty,2 \end{CD} \qquad \begin{aligned} \zm_{\widetilde{\zr}_1}(s)&= -s+2\\ \zs_{\widetilde{\zr}_1}(z)&= \frac{-z}{2z+1} \end{aligned}} \end{equation} | (6.1) |
| \begin{equation}\label{lin:rhotwo} {\begin{aligned} \zm_{\zr_2}(s)&= -s-2\\ \zs_{\zr_2}(z)&= \frac{z}{2z-1} \end{aligned} \qquad \begin{CD} \infty,-1 @> \zm_{\zr_2}> > \infty,-1\\ @V\zm_{f_0}VV @VV\zm_{f_0}V\\ \infty,0 @> \zm_{\widetilde{\zr}_2}> > \infty,0 \end{CD} \qquad \begin{aligned} \zm_{\widetilde{\zr}_2}(s)&= -s\\ \zs_{\widetilde{\zr}_2}(z)&= -z \end{aligned}} \end{equation} | (6.2) |
| \begin{equation}\label{lin:rhothree} {\begin{aligned} \zm_{\zr_3}(s)&= \frac{-s}{2s+1}\\ \zs_{\zr_3}(z)&= -z+2 \end{aligned} \qquad \begin{CD} \infty,-1 @> \zm_{\zr_3}> > -\frac{1}{2},-1\\ @V\zm_{f_0}VV @VV\zm_{f_0}V\\ \infty,0 @> \zm_{\widetilde{\zr}_3}> > 1,0 \end{CD} \qquad \begin{aligned} \zm_{\widetilde{\zr}_3}(s)&= \frac{s}{s-1}\\ \zs_{\widetilde{\zr}_3}(z)&= -z-1 \end{aligned}} \end{equation} | (6.3) |
Fundamental domains for $ G_{f_0}$, $ G_{f_0}^+$, $ \widetilde{G}_{f_0}$ and $ \widetilde{G}_{f_0}^+$. Still focusing on our example map $ f_0$, we now have explicit expressions for $ \zs_{\zr_i}$ and $ \zs_{\widetilde{\zr}_i}$ for $ i\in \{1,2,3\}$. These maps are all reflections. Let $ \za_i$ and $ \widetilde{\za}_i$ denote the reflection axes of $ \zs_{\zr_i}$ and $ \zs_{\widetilde{\zr}_i}$ (their fixed point sets) for $ i\in \{1,2,3\}$. One verifies that the unshaded triangle in the left side of Fig. 10 is a fundamental domain for the action of $ G_{f_0}$ on $ \mathbb{H}$. The two triangles in the left side of Fig. 10 form a fundamental domain for the action of $ G_{f_0}^+$ on $ \mathbb{H}$. This shows that the image of $ G_{f_0}$ in $ \text{PGL}(2,\mathbb{Z})$ and the image of $ G_{f_0}^+$ in $ \text{PSL}(2,\mathbb{Z})$ both have index 6. The right side of Fig. 10 shows fundamental domains for $ \widetilde{G}_{f_0}$ and $ \widetilde{G}_{f_0}^+$, the images of $ G_{f_0}$ and $ G_{f_0}^+$ under the extended modular group virtual endomorphism.
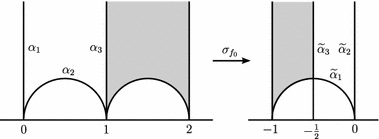
Images of cusps under $ \zs_{f_0}$. For our example map $ f_0$, we have that $ \zs_{f_0}\circ \zs_{\zr_i}=\zs_{\widetilde{\zr}_i}\circ \zs_{f_0}$ for $ i\in \{1,2,3\}$. It follows that $ \zs_{f_0}(\za_i)\subseteq \widetilde{\za}_i$ for $ i\in \{1,2,3\}$. Using the continuity of $ \zs_{f_0}$ on the Weil–Petersson completion $ \mathbb{H}^*$ of $ \mathbb{H}$, it follows that $ \zs_{f_0}$ maps the common endpoint 0 of $ \za_1$ and $ \za_2$ to the common endpoint 0 of $ \widetilde{\za}_1$ and $ \widetilde{\za}_2$. (We already essentially knew this through evaluation of $ \zm_{f_0}$.) Similarly, $ \zs_f(1)=\infty$ and $ \zs_{f_0}(\infty)=-\frac{1}{2}+\frac{1}{2}i$. This last equation shows that in special cases such as this, it is possible to determine the image in $ \mathbb{H}$ of a cusp under the pullback map of a NET map.
The degree of the induced map $ \hat{\zs}_f\co \mathbb{H}^*/G_f^+\to \mathbb{H}^*/\widetilde{G}_f^+$. Suppose $ f$ is a general NET map. We make the further assumption that $ \zs_f$ is nonconstant. In this case, the map $ \zs_f\co \mathbb{H}^*\to \mathbb{H}^*$ induces a nonconstant map $ \hat{\zs}_f\co \mathbb{H}^*/G_f^+\to \mathbb{H}^*/\widetilde{G}_f^+$ of compact Riemann surfaces. The degree of $ \hat{\zs}_f$ can be calculated as follows. Let $ y$ be a cusp in $ \mathbb{H}^*/\widetilde{G}_f^+$. Then \begin{equation*} \deg(\hat{\zs}_f)=\sum_{\hat{\zs}_f(x)=y}^{}\deg_x(\hat{\zs}_f). \end{equation*}
Returning to our example map $ f_0$, we take $ y$ to be the image in $ \mathbb{H}^*/\widetilde{G}_{f_0}^+$ of 0. Then there is only one value for $ x$, the image of 0 in $ \mathbb{H}^*/G_{f_0}^+$. Because the multiplier for slope $ \infty$ ($ =-\frac{1}{0}$) is 1, we see that a generator of the stabilizer of 0 in $ G_{f_0}^+$ maps to a generator of the stabilizer of 0 in $ \widetilde{G}_{f_0}^+$. Thus $ \deg(\hat{\zs}_{f_0})=1$.
Construction of $ \zs_{f_0}$. Finally, we determine $ \sigma_{f_0}$. We first construct a candidate $ \zs\co \mathbb{H}\to \mathbb{H}$, which we will eventually see is $ \zs_{f_0}$. By the Riemann mapping theorem there exists a unique analytic bijection $ \zs$ which maps the hyperbolic triangle with vertices 0, 1 and $ \infty$ to the hyperbolic triangle with vertices 0, $ \infty$ and $ -\frac{1}{2}+\frac{1}{2}i$ so that $ \zs(0)=0$, $ \zs(1)=\infty$ and $ \zs(\infty)=-\frac{1}{2}+\frac{1}{2}i$. We then extend the definition of $ \zs$ to all of $ \mathbb{H}$ using the reflection principle. This defines $ \zs\co \mathbb{H}\to \mathbb{H}$.
Just as $ \zs_{f_0}$ induces the map $ \hat{\zs}_{f_0}\co \mathbb{H}^*/G_{f_0}^+\to \mathbb{H}^*/\widetilde{G}_{f_0}^+$, the map $ \zs$ induces a map $ \hat{\zs}\co \mathbb{H}^*/G_{f_0}^+\to \mathbb{H}^*/\widetilde{G}_{f_0}^+$. These Riemann surfaces both have genus 0. Both $ \hat{\zs}_{f_0}$ and $ \hat{\zs}$ have degree 1 and they agree at the three cusps. Thus they are equal. Therefore the restriction of $ \zs_{f_0}$ to $ \za_1$, for example, agrees with the restriction of $ \zs$ to $ \za_1$. It follows that $ \zs_{f_0}=\zs$.
7. Dynamics on Curves in Degree 2

In this section we investigate the dynamics on curves for the set of NET maps with degree 2 and exactly one critical postcritical point. We will then indicate how to extend this result to all NET maps with degree 2 and hyperbolic orbifolds.
Theorem 8.
Let $ g$ be a NET map with degree 2 and exactly one critical postcritical point. Let $ \zm_g$ be the slope function of $ g$. Then we have the following.- (1) If $ g$ is combinatorially equivalent to a rational map, then $ \zm_g$ has a global attractor containing at most four slopes.
- (2) Suppose that
$ g$ is not combinatorially equivalent to a rational map. Let
$ s\in \overline{\mathbb{Q}}=\mathbb{Q}\cup \{\infty\}$ be the slope of the obstruction of $ g$. Let
$ \zh$ be a generator of the cyclic group of $ g$-liftable
elements in the modular group of $ g$ which stabilize
$ s$. Then under iteration, a slope either becomes undefined (that
is, the corresponding curve is trivial or peripheral), or lands in either
- (a) $ \{s\}$, or
- (b) $ \{s\}\cup \{\zh^m(r):m\in \mathbb{Z}\}$ for some $ r\in \overline{\mathbb{Q}}$ such that $ \zm_g(\zh^m(r))=\zh^{m+n}(r)$ for every integer $ m$ and some integer $ n$.
Proof.
Let $ f$ be the NET map $ f_0$ of Sect. 6. As in Sect. 6, let $ G_f$ denote the subgroup of liftables for $ f$ in the extended modular group $ \text{EMod}(S^2,P(f))$.Figure 10 in effect describes the pullback map $ \zs_f$. On the left are two triangles in a tesselation $ T_f$ of the Weil–Petersson completion $ \mathbb{H}^*$ of $ \mathbb{H}$ by fundamental domains for the action of $ G_f$. The pullback map $ \zs_f$ maps the unshaded, respectively shaded, triangle on the left to the unshaded, respectively shaded, triangle on the right. Extending by the reflection principle, we see that $ \zs_f$ maps every triangle of $ T_f$ into a triangle of $ T_f$.
Theorem 7 implies that $ g$ lies in the same impure Hurwitz class as $ f$. If $ g$ is conjugate to $ f$, then clearly there is a tesselation $ T_g$ of $ \mathbb{H}^*$ by fundamental domains for the action of $ G_g$ on $ \mathbb{H}^*$ such that $ \zs_g$ maps every triangle of $ T_g$ into a triangle of $ T_g$. Suppose that $ g=f\circ \zv$ for some map $ \zv$ representing an element of $ \text{Mod}(S^2,P(f))$. Then $ \zs_g=\zs_\zv\circ \zs_f$. One easily verifies that $ G_g=G_f$ and that $ \zs_\zv$ acts as an automorphism of $ T_f$. Thus $ \zs_g$ maps every triangle of $ T_g$ into a triangle of $ T_g$ in this case also. We conclude that the map $ g$ of Theorem 8 maps every triangle of $ T_g$ into a triangle of $ T_g$. It follows that every iterate of $ \zs_g$ maps every triangle of $ T_g$ into a triangle of $ T_g$.
Now suppose that $ g$ is combinatorially equivalent to a rational map. Then $ \zs_g$ has a fixed point $ \zt\in \mathbb{H}$. Let $ r\in \overline{\mathbb{Q}}$. Let $ t$ be a triangle of $ T_g$ which has $ r$ as a vertex. Let $ z$ be a point in the interior of $ t$. Then the points $ z$, $ \zs_g(z)$, $ \zs_g^2(z),\ldots$ converge to $ \zt$. So they eventually enter the star of $ \zt$ in $ T_g$ (the union of triangles containing $ \tau$). Because iterates of $ \zs_g$ map $ t$ into triangles of $ T_g$, it follows that $ t$ eventually enters the star of $ \zt$ in $ T_g$. Because $ \zs_g$ is continuous on $ \mathbb{H}^*$, it follows that $ r$ eventually enters the star of $ \zt$ in $ T_g$. This star has at most two triangles and at most four vertices. Since $ \zs_g$ and $ \zm_g$ are conjugate on $ \overline{\mathbb{Q}}$ via $ p/q \mapsto -q/p$, this proves statement 1.
Now suppose that $ g$ is not combinatorially equivalent to a rational map. So $ g$ has an obstruction. The pullback map $ \zs_g$ fixes the negative reciprocal of the slope of this obstruction. We find it convenient for this fixed point to be $ \infty $. So we replace the map $ f$ two paragraphs above by a conjugate so that the new pullback map is $ \zs_f$ conjugated by $ z\mapsto -1/z$. Arguing as two paragraphs above, we find that Fig. 11 describes $ \zs_g$ in the same way that Fig. 10 describes $ \zs_f$. The $ n$ in Fig. 11 is an integer. Any integer is possible. The case $ n=0$ is the case in which $ g$ is conjugate to $ f$.
Arguing as in the case in which $ g$ is unobstructed, we find that every element of $ \overline{\mathbb{Q}}$ eventually enters the star in $ T_g$ of $ \infty$ under the iterates of $ \zs_g$. Hence it only remains to determine the action of $ \zs_g$ on integers.
We have that $ \zs_g(-1)=n$. Using the reflection principle, we see that $ \zs_g(m)=m+n+1$ for every odd integer $ m$. Similarly, $ \zs_g(m)=m+n+1+i$ for every even integer $ m$. Furthermore, the stabilizer of $ \infty$ in the subgroup of modular group liftables for $ g$ has a generator which acts on $ \mathbb{H}$ as $ z\mapsto z+2$.
Now suppose that $ n$ is even. Then $ \zs_g$ maps odd integers to even integers, and it maps even integers into $ \mathbb{H}$. So every integer eventually leaves $ \overline{\mathbb{Q}}$. We are in the situation of case 2a.
Finally suppose that $ n$ is odd. Then $ \zs_g$ maps odd integers to odd integers, and it maps even integers into $ \mathbb{H}$. It follows that we are in case 2$ b$ with $ n+1$ here being 2 times $ n$ there.
The only thing left to prove is that case 1 actually occurs, namely, that there exists a rational NET map with degree 2 and exactly one critical postcritical point. An example of such a map is $ f(z)=z^2+i$.
This proves Theorem 8. ⬜
It was noted in the above proof that the map $ f_0$ of Sect. 6 corresponds to the case $ n=0$. Since 0 is even, the map $ f_0$ falls into case 2a. Thus $ f_0$ provides an example of an obstructed Thurston map with hyperbolic orbifold whose pullback map on curves has a finite global attractor consisting of just the obstruction.
We next indicate how Theorem 8 can be extended to all NET maps with degree 2 and hyperbolic orbifold. Theorem 7 and the paragraph preceding it imply that there are two impure Hurwitz classes of NET maps with hyperbolic orbifolds. The impure Hurwitz class of maps with one critical postcritical point is represented by the map $ f_0$ of Sect. 6, and the proof of Theorem 8 uses $ f_0$. The impure Hurwitz class of maps with two critical postcritical points is represented by the rabbit, and in the same way it is possible to use the rabbit to prove the corresponding result for these maps.
We discuss this extension in this paragraph. Let $ f(z)=z^2+c_R$ denote the rabbit polynomial of the introduction. Figure 2 gives a NET map presentation diagram for $ f$. Arguing as in Sect. 6, we find that Fig. 12 provides an analog to Fig. 10 for the pullback map $ \zs_f$ of $ f$. More precisely, $ \zs_f$ maps the unshaded, respectively shaded, triangle in the left side of Fig. 12 bijectively to the unshaded, respectively shaded, triangle in the right side of Fig. 12 with $ \zs_f(0)=\infty$, $ \zs_f(\infty)=-1$, $ \zs_f(-1)=0$ and $ \zs_f(-2)=-\frac{1}{2}+\frac{1}{2}i$. The last equation provides another example of an exact evaluation of a pullback map at an element of $ \overline{\mathbb{Q}}$ when that value lies in $ \mathbb{H}$. Whereas before we worked with a tesselation by triangles, now we work with a tesselation by quadrilaterals, those determined by the union of the two triangles in the left side of Fig. 12. From here the argument proceeds as before. The result is essentially the same, although the statement must be modified a bit. The main difference is that case 2a does not occur here.
We say a few more words about the pullback map $ \zs_f$ for the rabbit in this paragraph. The blue curve in the left side of Fig. 1 has slope 0 relative to Fig. 2. This curve lies in a 3-cycle of curves for the pullback map on curves. In terms of slopes, $ \zm_f(0)=1$, $ \zm_f(1)=\infty$ and $ \zm_f(\infty)=0$. Because points of $ \partial \mathbb{H}$ correspond to negative reciprocals of slopes, these equations correspond to the equations $ \zs_f(\infty)=-1$, $ \zs_f(-1)=0$ and $ \zs_f(0)=\infty$, just as in the previous paragraph. Because $ \zs_f$ maps the quadrilateral with vertices $ -2$, $ -1$, 0 and $ \infty$ into itself, its fixed point is in this quadrilateral. Figure 4 further shows that this fixed point has small imaginary part (within the Euclidean circle centered at $ (-1,0)$ with radius $ \sqrt{2}$).
Since the fixed point $ \zt$ of $ \zs_f$ is in the interior of the quadrilateral which is the union of the two triangles on the left side of Fig. 12, the star of $ \zt$ in this tesselation consists of just this quadrilateral. So for any $ t\in \overline{\mathbb{Q}}$, either there exists a positive integer $ n$ with $ \zm_f^{\circ n}(t) = \odot$, or for $ n$ sufficiently large $ \zs_f^{\circ n}(t)\in \{0,-1,\infty\}$. Thus there is a finite global attractor consisting of points whose slopes correspond to $ 0$, $ 1$ and $ \infty$. This gives another proof of Theorem 2.
8. The Extended Half-Space Theorem

The goal of this section is to sketch a proof of the extended half-space theorem. After filling in the details, the intervals mentioned in the theorem can be explicitly determined. See the discussion at the end of Sect. 1. Here is a qualitative statement of the theorem.
Theorem 9.
(Extended Half-Space Theorem) Let $ f$ be a NET map with slope function $ \zm_f$. Let $ \frac{p}{q}\in \overline{\mathbb{Q}}$, and suppose that either $ \zm_f(\frac{p}{q})=\frac{p}{q}$ and $ \zd_f(\frac{p}{q})\ne 1$ or that $ \zm_f(\frac{p}{q})=\odot$. Then there exists an interval in $ \mathbb{R}\cup \{\infty\}$ containing $ -\frac{q}{p}$ which contains no negative reciprocals of obstructions for $ f$ other than possibly $ -\frac{q}{p}$.To begin a sketch of the proof of this, we recall the setting of the half-space theorem. Let $ s_1$ be the slope of a simple closed curve in $ S^2-P(f)$ whose preimage under $ f$ contains a connected component which is essential and nonperipheral (if no such $ s_1$ exists, $ f$ is unobstructed, by Thurston's characterization theorem). Let $ s'_1=\zm_f(s_1)$, and suppose that $ s'_1\ne s_1$. In this situation the half-space theorem supplies an open half-space $ H_1$ in the upper half-plane which contains no fixed point of $ \zs_f$ and whose boundary's interior contains $ -1/s_1$ but no negative reciprocal of a obstruction for $ f$. The half-space $ H_1$ depends only on $ s_1$, $ s'_1$ and the multiplier $ \zd_f(s_1)$. We call such a half-space an excluded half-space.
Let $ t$ be an extended rational number which is not mapped to a different extended rational number by $ \zs_f$. We will use functional equations satisfied by $ \zs_f$ to produce excluded half-spaces near $ t$ so that the collection of all extended real numbers excluded by these half-spaces together with $ t$ forms an open interval about $ t$ in $ \mathbb{R}\cup \{\infty\}$.
We consider the simplest case, the case in which $ t=\infty$. The general case can be gotten from this by applying an element of $ \text{PSL}(2,\mathbb{Z})$ to $ t$. Keep in mind that points of $ \overline{\mathbb{Q}}$ in the boundary of $ \mathbb{H}$ are to be viewed as negative reciprocals of slopes. So either $ \zm_f(0)=0$ or $ \zm_f(0)=\odot$. Let $ \zg$ be a simple closed curve in $ S^2-P(f)$ with slope 0. Let $ d$ be the degree with which $ f$ maps every connected component of $ f^{-1}(\zg)$ to $ \zg$. Let $ c$ be the number of these connected components which are neither inessential nor peripheral. Theorem 7.1 of [Cannon et al.2012], for example, yields the functional equation $ \zs_f\circ \zv^d=\zv^c\circ \zs_f$, where $ \zv(z)=z+2$. We have that $ \zd_f(0)=\frac{c}{d}$. By hypothesis, $ \frac{c}{d}\ne 1$. For convenience we consider the case that $ \frac{c}{d}< 1$, so $ c< d$.
Let $ t_1=-\frac{1}{s_1}$ and $ t'_1=-\frac{1}{s'_1}$, where $ s_1$ and $ s'_1$ are as above. Since $ t=\infty$, it is natural to assume that $ t_1\ne \infty$. For simplicity, we also assume that $ t'_1\ne \infty$. Let $ B_1$ and $ B'_1$ be closed horoballs at $ t_1$ and $ t'_1$ as in the statement of the half-space theorem in Cannon et al. ([Cannon et al.2012], Theorem 5.6). Let $ r$ be the Euclidean radius of $ B_1$, and let $ r'$ be the Euclidean radius of $ B'_1$.
If $ r> r'$, then our excluded half-space $ H_1$ is unbounded in the Euclidean metric, and so we already have an open neighborhood of $ \infty$ in $ \mathbb{R}\cup \{\infty\}$ which contains no negative reciprocals of obstructions. So we assume that $ r\le r'$. The case in which $ r=r'$ can be handled as follows. In this case $ H_1$ is bounded by a vertical Euclidean ray with endpoint the average value of $ t_1$ and $ t'_1$. This gives us an unbounded interval of real numbers which contains no negative reciprocals of obstructions. Using the fact that $ c< d$, we replace $ t_1$ and $ t'_1$ by their images under an appropriate power of $ \zv^d$ and $ \zv^c$ (possibly negative) so that the order of these images is opposite to the order of $ t_1$ and $ t'_1$. The resulting excluded half-space and $ H_1$ combine to produce an open neighborhood of $ \infty$ in $ \mathbb{R}\cup \{\infty\}$ containing no negative reciprocals of obstructions. This establishes the existence of such an interval. Hence we assume that $ r< r'$. In this case $ H_1$ lies within a Euclidean semicircle. Let $ C_1$ and $ R_1$ be the center and radius of this semicircle. See Fig. 13, which assumes that $ t_1> t'_1$.
Now we apply the functional equation $ \zs_f\circ \zv^d=\zv^c\circ \zs_f$. Set $ t_2=\zv^d(t_1)$ and $ t'_2=\zv^c(t'_1)$. Then the equation $ \zm_f(s_1)=s'_1$ implies that $ \zs_f(t_1)=t'_1$, and so $ \zs_f(t_2)=t'_2$. Because $ t_1> t'_1$, and $ d> c$, we have that $ t_2> t'_2$.
In this paragraph we show that the half-space theorem applies to $ t_2$ and $ t'_2$ using the horoballs $ B_2=\zv^d(B_1)$ and $ B'_2=\zv^c(B'_1)$. We have the equation $ \zs_f\circ \zv^d=\zv^c\circ \zs_f$. This is induced by a homotopy equivalence of the form $ \zf^d\circ f\sim f\circ \zf^c$, where $ \zf$ is a Dehn twist about a curve with slope $ 0$. The equation $ t_2=\zv^d(t_1)$ implies that if $ \zg_1$ is a simple closed curve in $ S^2-P (f)$ with slope $ s_1=-1/t_1$, then $ \zg_2=\zf^{-d}(\zg_1)$ is a simple closed curve in $ S^2-P(f)$ with slope $ s_2=-1/t_2$. A corresponding statement holds for $ \zf^{-c}$. Now the homotopy equivalence $ \zf^d\circ f\sim f\circ \zf^c$ shows that if $ c_2$ is the number of connected components of $ f^{-1}(\zg_2)$ which are neither inessential nor peripheral and if $ d_2$ is the degree with which $ f$ maps these components to $ \zg_2$, then $ c_2=c_1$ and $ d_2=d_1$. So $ \zd_f(s_2)=\zd_f(s_1)$. Combining this with Corollary 6.2 of [Cannon et al.2012], which shows how elements of $ \text{PGL}(2,\mathbb{Z})$ map horoballs to horoballs, it follows that the half-space theorem applies to $ t_2$ and $ t'_2$ using the horoballs $ B_2=\zv^d(B_1)$ and $ B'_2=\zv^c(B'_1)$. Hence we obtain another excluded half-space $ H_2$ corresponding to the horoballs $ B_2$ and $ B'_2$ at $ t_2$ and $ t'_2$ with Euclidean radii $ r$ and $ r '$.
We want $ H_1\cap H_2\ne \emptyset$ because then the open intervals in $ \mathbb{R}$ determined by $ H_1$ and $ H_2$ can be combined to form a larger interval. Since $ t_2> t_1$ as in Fig. 13, $ H_1\cap H_2\ne \emptyset$ if and only if $ C_1+R_1> C_2-R_2$. We make an explicit computation based on this and find that \begin{equation*} H_1\cap H_2\ne \emptyset\Longleftrightarrow t_1-t'_1> d\big(\sqrt{r'/r}-1\big)+c\big(1-\sqrt{r/r'}\big). \end{equation*}
Suppose that the last inequality is satisfied. Then because \begin{equation*} t_2-t'_2=t_1+2d-t'_1-2c=t_1-t'_1+2(d-c)> t_1-t'_1, \end{equation*} the inequality in the next-to-last display is satisfied with $ t_1-t'_1$ replaced by $ t_2-t'_2$. Inductively, we conclude that if $ H_1\cap H_2\ne \emptyset$, then $ f$ has no obstruction $ s$ with $ -\frac{1}{s}> C_1-R_1$. Furthermore, the last display shows that the differences $ t_1-t'_1$ increase without bound under iteration, and so it is possible to find $ t_1$ such that $ H_1\cap H_2\ne \emptyset$.
This obtains an unbounded interval of positive real numbers which contains no negative reciprocals of obstructions. Symmetry yields a corresponding interval of negative real numbers. This is the gist of the extended half-space theorem. It remains to make the estimates explicit for computation. This is a bit tedious, but straightforward.
Theorem 9 is false if $ \delta_f(p/q)=1$; counterexamples are found among maps in 21HClass3 and 31Hclass5, 6, 9.
Acknowledgements.
The authors gratefully acknowledge support from the American Institute for Mathematics, which funded the "SQuaRE" workshops in the summers of 2013–15 during which much of this joint work was conducted. Russell Lodge was also supported by the Deutsche Forschungsgemeinschaft. Kevin Pilgrim was also supported by Simons Grant #245269. Sarah Koch was also supported by the NSF and the Sloan Foundation.References
[Bonnot et al.2012] Bonnot, S., Braverman, M., Yampolsky, M.: Thurston equivalence to a rational map is decidable. Mosc. Math. J. 12 (4), 747–763 (2012)
[Bartholdi and Dudko2017] Bartholdi, L., Dudko, D.: Algorithmic aspects of branched coverings. arXiv:1512.05948 (2017)
[Bartholdi and Nekrashevych2006] Bartholdi, L., Nekrashevych, V.: Thurston equivalence of topological polynomials. Acta Math. 197 , 1–51 (2006)
[Buff et al.2009] Buff, X., Epstein, A., Koch, S., Pilgrim, K.: On Thurston's pullback map. In: Schleicher, D. (ed.) Complex Dynamics—Families and Friends, pp. 561–583. A. K. Peters, Wellesley (2009)
[Cannon et al.2012] Cannon, J.W., Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Nearly Euclidean Thurston maps. Conform. Geom. Dyn. 16 , 209–255 (2012) (electronic)
[Douady and Hubbard1993] Douady, A., Hubbard, J.H.: A proof of Thurston's topological characterization of rational functions. Acta Math. 171 , 263–297 (1993)
[Floyd et al.2017a] Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Presentations of NET maps. arXiv:1701.00443 (2017a)
[Floyd et al.2017b] Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Modular groups, Hurwitz classes and dynamic portraits of NET maps. arXiv:1703.03983 (2017b)
[Kameyama2001] Kameyama, A.: The Thurston equivalence for postcritically finite branched coverings. Osaka J. Math. 38 , 565–610 (2001)
[Kelsey and Lodge2017] Kelsey, G., Lodge, R.: Quadratic Thurston maps with few postcritical points. arXiv:1704.03929 (2017)
[Koch2013] Koch, S.: Teichmüller theory and critically finite endomorphisms. Adv. Math. 248 , 573–617 (2013)
[Koch et al.2016] Koch, S., Pilgrim, K.M., Selinger, N.: Pullback invariants of Thurston maps. Trans. Amer. Math. Soc. 368 , 4621–4655 (2016)
[Lehner1964] Lehner, J.: Discontinuous Groups and Automorphic Functions. Mathematical Surveys, vol. 8. American Mathematical Society, Providence (1964)
[Levy1985] Levy, S.: Critically finite rational maps. PhD thesis, Princeton University (1985)
[Lodge2015] Lodge, R.: Boundary values of the Thurston pullback map. Conform. Geom. Dyn. 17 , 77–118 (2013) (electronic)
[Meyer2014] Meyer, D.: Unmating of rational maps, sufficient criteria and examples. In: Bonifant, A., Lyubich, M., Sutherland, S. (eds.) Frontiers in Complex Dynamics: In Celebration of John Milnor's 80th Birthday, pp. 197–233. Princeton University Press, Princeton (2014)
[Milnor2004] Milnor, J.: Pasting together Julia sets: a worked-out example of mating. Exp. Math. 13 (1), 55–92 (2004)
[Pilgrim2003] Pilgrim, K.M.: Combinations of Complex Dynamical Systems. Springer Lecture Notes in Mathematics, vol. 1827. Springer, Berlin (2003)
[Pilgrim2012] Pilgrim, K.M.: An algebraic formulation of Thurston's characterization of rational functions. Ann. Fac. Sci. Toulouse Math. 21 (5), 1033–1068 (2012)
[Saenz Maldonado2012] Saenz Maldonado, E.A.: On nearly Euclidean Thurston maps. Ph.D. Thesis, Virginia Tech (2012)
[Selinger2012] Selinger, N.: Thurston's pullback map on the augmented Teichmüller space and applications. Invent. Math. 189 , 111–142 (2012)
[NET maps2016] NET maps web site: (2016)
- 99
- × Bartholdi, L.: IMG, software package for GAP. (2014)
- × Bonnot, S., Braverman, M., Yampolsky, M.: Thurston equivalence to a rational map is decidable. Mosc. Math. J. 12 (4), 747–763 (2012)
- × Bartholdi, L., Dudko, D.: Algorithmic aspects of branched coverings. arXiv:1512.05948 (2017)
- × Bartholdi, L., Nekrashevych, V.: Thurston equivalence of topological polynomials. Acta Math. 197 , 1–51 (2006)
- × Buff, X., Epstein, A., Koch, S., Pilgrim, K.: On Thurston's pullback map. In: Schleicher, D. (ed.) Complex Dynamics—Families and Friends, pp. 561–583. A. K. Peters, Wellesley (2009)
- × Cannon, J.W., Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Nearly Euclidean Thurston maps. Conform. Geom. Dyn. 16 , 209–255 (2012) (electronic)
- × Douady, A., Hubbard, J.H.: A proof of Thurston's topological characterization of rational functions. Acta Math. 171 , 263–297 (1993)
- × Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Presentations of NET maps. arXiv:1701.00443 (2017a)
- × Floyd, W.J., Parry, W.R., Pilgrim, K.M.: Modular groups, Hurwitz classes and dynamic portraits of NET maps. arXiv:1703.03983 (2017b)
- × Kameyama, A.: The Thurston equivalence for postcritically finite branched coverings. Osaka J. Math. 38 , 565–610 (2001)
- × Kelsey, G., Lodge, R.: Quadratic Thurston maps with few postcritical points. arXiv:1704.03929 (2017)
- × Koch, S.: Teichmüller theory and critically finite endomorphisms. Adv. Math. 248 , 573–617 (2013)
- × Koch, S., Pilgrim, K.M., Selinger, N.: Pullback invariants of Thurston maps. Trans. Amer. Math. Soc. 368 , 4621–4655 (2016)
- × Lehner, J.: Discontinuous Groups and Automorphic Functions. Mathematical Surveys, vol. 8. American Mathematical Society, Providence (1964)
- × Levy, S.: Critically finite rational maps. PhD thesis, Princeton University (1985)
- × Lodge, R.: Boundary values of the Thurston pullback map. Conform. Geom. Dyn. 17 , 77–118 (2013) (electronic)
- × Meyer, D.: Unmating of rational maps, sufficient criteria and examples. In: Bonifant, A., Lyubich, M., Sutherland, S. (eds.) Frontiers in Complex Dynamics: In Celebration of John Milnor's 80th Birthday, pp. 197–233. Princeton University Press, Princeton (2014)
- × Milnor, J.: Pasting together Julia sets: a worked-out example of mating. Exp. Math. 13 (1), 55–92 (2004)
- × Pilgrim, K.M.: Combinations of Complex Dynamical Systems. Springer Lecture Notes in Mathematics, vol. 1827. Springer, Berlin (2003)
- × Pilgrim, K.M.: An algebraic formulation of Thurston's characterization of rational functions. Ann. Fac. Sci. Toulouse Math. 21 (5), 1033–1068 (2012)
- × Saenz Maldonado, E.A.: On nearly Euclidean Thurston maps. Ph.D. Thesis, Virginia Tech (2012)
- × Selinger, N.: Thurston's pullback map on the augmented Teichmüller space and applications. Invent. Math. 189 , 111–142 (2012)
- × NET maps web site: (2016)