Received: 7 October 2016 / Revised: 30 June 2017 / Accepted: 8 October 2017
Soyuza Pechatnikov Str., 16 St. Petersburg Russian Federation
nikaanspb@gmail.com, Mikhail Shkolnikov Section de Mathématiques University of Geneva
Route de Drize 7, Villa Battelle 1227 Carouge Switzerland
Abstract
where the sum runs by all $ a,b,c,d\in{\mathbb{Z}}_{\geq 0}$ such that $ ad-bc=1$. We present a proof of these formulae and list several directions for the future studies.
Keywords
pi, Special linear group, Summation, Tropical geometry, Lattice geometry
1.
History: Geometric Approach to $ \pi$ 
why investigate such problems, given that irrational numbers
do not even exists?
Apocryphally attributed to Leopold Kronecker by Ferdinand Lindemann
The digit computation of $ \pi$ probably is one of the oldest research directions in mathematics. Due to Archimedes, we may consider the inscribed and circumscribed equilateral polygons for the unit circle. Let $ q_n$ (resp., $ Q_n$) be the perimeter of such an inscribed (resp., circumscribed) $ 3\cdot2^n$-gon. The sequences $ \{q_n\},\{Q_n\}$ obey the recurrence \begin{eqnarray*}Q_{n+1}=\frac{2q_nQ_n}{q_n+Q_n}, q_{n+1}=\sqrt{q_nQ_{n+1}}\end{eqnarray*} and both converge to $ 2\pi$. However this gives no closed formula.
A major breakthrough was made by Euler, Swiss-born (Basel) German–Russian mathematician. In his Saint-Petersburg Academy of Science talk (December 5, 1735) and, then, paper ([Euler1740]), he calculated ( literally ) that
| \begin{eqnarray} \label{eqspseuler} \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6}. \end{eqnarray} | (1) |
Euler's idea was to use the identity \begin{eqnarray*} 1-\frac{z^2}{6}+\dots=\frac{\sin(z)}{z}=\prod_{n=1}^\infty \Big(1-\frac{z^2}{n^2 \pi^2}\Big), \end{eqnarray*} where the first equality is the Taylor series and the second equality is due to the fact that these two functions have the same set of zeroes. Equating the coefficients in $ z^2$, we get (1) . This reasoning was not justified until Weierstrass, but there appeared many other proofs. A nice exercise to get (1) is by considering the residues of $ \frac{\cot(\pi z)}{z^2}$.
We would like to mention here a rather elementary geometric proof of (1) which is contained in Cauchy's notes, ([Cauchy1821]).
Let $ \alpha=\frac{\pi}{2m+1}$. Then $ \sin (n\alpha)< n\alpha< \operatorname{tan} (n\alpha)$ for $ n=1,\dots,m$, see Fig. 1. Therefore, $ \cot^2(n\alpha)\leq \frac{1}{n^2\alpha^2}\leq \csc^2(n\alpha)$. Writing $ \frac{\sin ((2m+1)x)}{(\sin x)^{2m+1}}$ as a polynomial in $ \cot x$ and using the fact that $ \frac{\pi n}{2m+1}$ are the roots of this polynomial by Vieta's Theorem, we can find the sum of $ \cot^2\alpha$ and $ \csc^2\alpha$ for $ \alpha=\frac{\pi n}{2m+1}, n=1,\dots, m$.
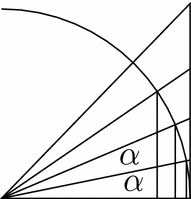
So, the above geometric consideration gives a two-sided estimate for $ \frac{1}{\pi^2}\sum_{n=1}^{m} \frac{1}{n^2}$ whose both sides converge to $ \frac{1}{6}$ as $ m\to\infty$.
2.
$ SL(2,\ZZ)$-Way to Cut Corners 
Recall that $ SL(2,\ZZ)$ is the set of matrices $ \begin{pmatrix} a & b \\ c& d \end{pmatrix}$ with $ a,b,c,d\in\ZZ$ and $ ad-bc=1$. With respect to the matrix multiplication, $ SL(2,\ZZ)$ is a group. We may identify such a matrix with the pair $ (a,b),(c,d)\in\ZZ^2$ of lattice vectors. These vectors span the parallelogram of area one and, consequently, give a basis of $ \ZZ^2$.
Definition 1.
A vector $ v\in\ZZ^2$ is primitive if its coordinates are coprime. A polygon $ P\subset \RR^2$ is called unimodular if- the sides of $ P$ have rational slopes;
- two primitive vectors in the directions of every pair of adjacent sides of $ P$ give a basis of $ \ZZ^2.$
Example 1.
The polygons $ P_0$ and $ P_1$ in Fig. 2 are unimodular.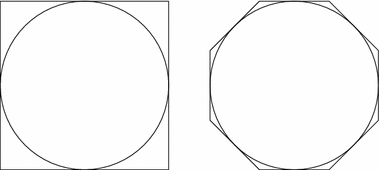
Let $ P_0=[-1,1]^2$, and $ D^2$ be the unit disk inscribed into $ P_0$, Fig. 2, left. Cutting all corners of $ P_0$ by tangent lines to $ D^2$ in the directions $ (\pm 1,\pm 1)$ results in the octagon $ P_1$, into which $ D^2$ is inscribed, Fig. 2, right.
Remark 1.
Note that if we cut a corner of $ P_0$ by any other tangent line to $ D^2$, then the resulting pentagon would not be unimodular. Then, a polygon's property of being unimodular is $ SL(2,\ZZ)$-invariant. This implies that if two sides of a corner are orthogonal to $ (a,b),(c,d)\in\ZZ^2$ with $ ad-bc=1$, then the only direction to cut this corner in order to have two unimodular corners after this procedure is to use a line orthogonal to $ (a+c,b+d)$.Definition 2.
For $ n\geq 0$, the unimodular polygon $ P_{n+1}$ circumscribing $ D^2$ is defined to be the result of cutting all $ 2^{n+2}$ corners of $ P_n$ by tangent lines to $ D^2$ in such a way that $ P_{n+1}$ is a unimodular polygon.Note that passing to $ P_{n+1}$ is unambiguous due to Remark 1.
Remark 2.
$ \lim_{n\rightarrow\infty}{\operatorname{Area}}(P_n)=\pi$, $ \lim_{n\rightarrow\infty}{\operatorname{Perimeter}}(P_n)=2\pi$.Example 2.
The primitive vector $ (1,1)$ is orthogonal to a side $ S$ of $ P_1$, belongs to the positive quadrant, and goes outside $ P_1$. Two vectors orthogonal to the neighboring to $ S$ sides of $ P_2$ are $ (2,1)$ and $ (1,2)$.Thus, we start with four vectors $ (1,0),(0,1),(-1,0),(0,-1)$—the outward directions for the sides of $ P_0$. To pass from $ P_n$ to $ P_{n+1}$, we order by angle all primitive vectors orthogonal to the sides of $ P_n$. Then, for each two neighboring vectors, we cut the corresponding corner of $ P_n$ by the tangent line to $ D^2$, orthogonal to their sum. In particular, every line with a rational slope tangent to $ D^2$ contains a side of $ P_n$ for $ n$ large enough.
We can reformulate the above observation as follows:
Lemma 1.
For all $ a,b,c,d\in \ZZ_{\geq 0}$ with $ ad-bc=1,$ such that $ (a,b),(c,d)$ belong to the same quadrant, there is a corner of $ P_n$ for some $ n\geq 0$ with sides orthogonal to $ (a,b)$ and $ (c,d).$ In $ P_{n+1}$, this corner is cropped by the line orthogonal to $ (a+c,b+d)$ and tangent to $ D^2.$Lemma 2.
In the above notation, the area of the cropped triangle is $ {1\over 2}f(a,b,c,d)^2.$
3.
Proofs of (Ж) and (ж) 
The area of the intersection of $ P_0{\setminus} D^2$ with the first quadrant is $ 1-\frac{\pi}{4}$. Therefore, Remark 2 and Lemma 2 prove (Ж) in the abstract.
Definition 3.
Let $ v$ be a primitive vector. We define the lattice length of a vector $ kv, k\in\RR_{\geq 0}$, to be $ k$.The lattice perimeter of $ P_n$ is the sum of the lattice lengths of its sides. For example, the usual perimeter of the octagon $ P_1$ is $ 16(\sqrt 2-1)$, and the lattice perimeter is $ 4\sqrt 2$.
Lemma 3.
The lattice perimeter of $ P_n$- tends to zero as $ n\to\infty$;
- is given by $ 4\big(2-\sum f(a,b,c,d)\big),$ where the sum runs over $ a,b,c,d\in\ZZ_{\geq 0}, ad-bc =1$, $ (a,b)$ and $ (c,d)$ are orthogonal to a pair of neighboring sides of some $ P_k$ with $ k< n$.
Proof.
The second statement follows from the cropping procedure by a direct computation. To prove the first statement, we note that for each primitive direction $ w$, the length of the side of $ P_n$ orthogonal to $ w$ tends to 0 as $ n\to\infty$. Therefore, for each $ N> 0$, the sum of the lattice lengths of the sides of $ P_n$ orthogonal to $ w$ with $ |w|< N$ tends to zero, and the rest part of the lattice perimeter of $ P_n$ is less than $ \frac{2\pi}{N}$ because of the definition of the lattice length. We conclude the proof by letting $ N\to\infty$. ⬜ Finally, (ж) follows from Lemmata 1, 3.
4.
Questions 
One may ask what happens for other powers of $ f(a,b,c,d).$ There is a partial answer in degree 3, which also reveals the source of our formulae.
For every primitive vector $ w\in\ZZ^2$, a tangent line to $ D^2$ orthogonal to $ w$ is given by $ w\cdot p+|w|=0.$ Consider a piecewise linear function $ F:D^2\rightarrow \RR$ defined as
| \begin{eqnarray} \label{eqspsf} F(p)=\inf_{w\in \ZZ^2\backslash{0}}(w\cdot p+|w|).\end{eqnarray} | (2) |
Performing verbatim the analysis of cropped tetrahedra applied to the graph of $ F$, one can prove the following lemma.
Lemma 4.
$ 4-2\sum f(a,b,c,d)^3=3\int_{D^2} F.$Now we describe the general idea behind (Ж), (ж). Denote by $ C\subset D^2$ the locus of all points $ p$ where the function $ F$ is not smooth. The set $ C$ is a locally finite tree (see Fig. 3). In fact, it is naturally a tropical curve (see [Kalinin and Shkolnikov2016], [Kalinin and Shkolnikov2017]). The numbers $ f(a,b,c,d)$ represent the values of $ F$ at the vertices of $ C$ and can be computed from the equations of tangent lines.
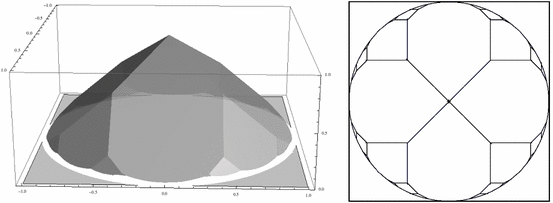
Below we list some directions, which we find interesting to explore. Coordinates on the space of compact convex domains For every compact convex domain $ \Omega$, we can define $ F_\Omega$ as the infimum of all support functions with integral slopes, exactly as in (2) . Consider the values of $ F_{\Omega}$ at the vertices of $ C_\Omega$, the corner locus of $ F_\Omega$. These values are the complete coordinates on the set of convex domains; therefore, the characteristics of $ \Omega$ (for example, the area) can be potentially expressed in terms of these values. How to relate these coordinates of $ \Omega$ with those of the dual domain $ \Omega^*$? Higher dimensions We failed to reproduce this line of arguments "by cropping" for three-dimensional bodies, but it seems that we need to sum up by all quadruples of vectors $ v_1,v_2,v_3,v_4$ such that $ \mathrm{ConvHull}(0,v_1,v_2,v_3,v_4)$ contains no lattice points. Zeta function We may consider the sum $ Z(s) = \sum f(a,b,c,d)^s$ as an analog of the Riemann zeta function. We can prove that $ Z(s)$ converges as long as $ s> 1/2$. Can we extend this function for complex values of $ s$? Other proofs It would be nice to give another proof of (Ж), (ж) with the methods which were used to prove (1) . Note that the vectors $ (a,b),(c,d)$ can be uniquely reconstructed from the vector $ (a+c,b+d)$, and our construction resembles the Farey sequence a lot. So we can think of $ f(a,b,c,d)$ as a kind of a measure on $ \QQ\cap [0,1]$, and can integrate a function along it. Can we interpret $ f(a,b,c,d)$ as a residue of a certain function at $ (a+b)+(c+d)i$? The Riemann zeta function is related to integers; could it be that $ f$ is related to the Gauss integers? Modular forms We can extend $ f$ to the whole $ SL(2,\ZZ)$. If both vectors $ (a,b),(c,d)$ belong to the same quadrant, we use the same definition. For $ (a,b),(c,d)$ from different quadrants, we could define \begin{eqnarray*} f(a,b,c,d)=\sqrt{a^2+b^2}+\sqrt{c^2+d^2}-\sqrt{(a-c)^2+(b-d)^2}. \end{eqnarray*} Then \begin{eqnarray*} \sum\limits_{m\in SL(2,\ZZ)}f(m) = \sum\limits_{\substack {a,b,c,d\in \ZZ \\ ad-bc=1}}f(a,b,c,d) \end{eqnarray*} is well defined. Can we naturally extend this function to the $ {\mathbb{C}}/SL(2,\ZZ)$? Can we make similar series for other lattices or tessellations of the plane?
Acknowledgements.
We want to thank God and the universe for these beautiful formulae. Also we would like to thank an anonymous referee for the idea to discuss the Euler formula, and Fedor Petrov and Pavol Ševera for fruitful discussions. The first author, Nikita Kalinin, is funded by the SNSF PostDoc.Mobility Grant 168647 and thanks Grant FORDECYT-265667 "Programa para un avance global e integrado de la matemática mexicana". Also, support from the Basic Research Program of the National Research University Higher School of Economics is gratefully acknowledged. The second author, Mikhail Shkolnikov is partially supported by the Grant 159240 of the Swiss National Science Foundation as well as by the National Center of Competence in Research SwissMAP of the Swiss National Science Foundation.References
[Euler1740] Euler, L.: De summis serierum reciprocarum. Commentarii academiae scientiarum Petropolitanae 7 , 123–134 (1740). (E41 in the Eneström index. An English translation can be found in arXiv:math/0506415v2)
[Kalinin and Shkolnikov2016] Kalinin, N., Shkolnikov, M.: Tropical curves in sandpiles. Comptes Rendus Mathematique 354 (2), 125–130 (2016)
[Kalinin and Shkolnikov2017] Kalinin, N., Shkolnikov, M.: Introduction to tropical series and wave dynamic on them (2017). arXiv:1706.03062
- 1
- × Cauchy, A.L.: Note VIII. Cours d'Analyse de l'École Royale Polytechnique; I.re Partie. Analyse algébrique (1821)
- × Euler, L.: De summis serierum reciprocarum. Commentarii academiae scientiarum Petropolitanae 7 , 123–134 (1740). (E41 in the Eneström index. An English translation can be found in arXiv:math/0506415v2)
- × Kalinin, N., Shkolnikov, M.: Tropical curves in sandpiles. Comptes Rendus Mathematique 354 (2), 125–130 (2016)
- × Kalinin, N., Shkolnikov, M.: Introduction to tropical series and wave dynamic on them (2017). arXiv:1706.03062