MathJax is loading, please wait
$ \renewcommand{\bar}{\overline} \newcommand\r{\mathbb{R}} \newcommand\c{\mathbb{C}} \newcommand\q{\mathbb{Q}} \newcommand\z{\mathbb{Z}} \newcommand\n{\mathbb{N}} \newcommand\A{\mathcal{A}} \newcommand\M{\mathcal{M}} \newcommand\d{\mathcal{D}} \newcommand\D{\mathcal{D_\gamma}} \newcommand{\di}{\operatorname{Discr}} \newcommand{\sspan}{\operatorname{Span}} \newcommand{\conv}{\operatorname{conv}} \newcommand{\iv}{\operatorname{lV}} \newcommand{\isin}{\operatorname{lsin}} \newcommand{\Isin}{\operatorname{ISIN}} \newcommand{\icos}{\operatorname{lcos}} \newcommand{\spann}{\operatorname{Span}} \newcommand{\itan}{\operatorname{ltan}} \newcommand{\gr}{\operatorname{Gr}} \newcommand{\iarctan}{\operatorname{larctan}} \newcommand{\lat}{\operatorname{Lat}} \newcommand{\grad}{\operatorname{grad}} \newcommand{\sign}{\operatorname{sign}} \newcommand{\id}{\operatorname{ld}} \newcommand{\sgn}{\operatorname{sgn}} \newcommand{\MOD}{\operatorname{mod}} \newcommand{\il}{\operatorname{l\ell}} \newcommand{\is}{\operatorname{lS}} \newcommand{\lcm}{\operatorname{lcm}} \newcommand{\ia}{\operatorname{l\alpha}} \newcommand{\paral}{\operatorname{Par}} \newcommand{\pcong}{\operatorname{\hat{\cong}}} $
Problem ContributionArnold Mathematical Journal

Received: 8 June 2017 / Revised: 13 January 2018 / Accepted: 22 January 2018

Open Problems on Configuration Spaces of Tensegrities
Oleg Karpenkov Department of Mathematical Sciences,
University of Liverpool,
Mathematical Sciences Building,
Liverpool L69 7ZL UK
karpenk@liverpool.ac.uk
Abstract
In this small paper we bring together some open problems related to the study of the configuration spaces of tensegrities, i.e. graphs with stresses on edges. These problems were announced in Doray et al. (Discrete Comput Geom 43:436–466, [Doray et al.2010]), Karpenkov et al. (ARS Math Contemp 6:305–322, [Karpenkov et al.2013]), Karpenkov (The combinatorial geometry of stresses in frameworks. arXiv:1512.02563 [math.MG], [Karpenkov2017]), and Karpenkov (Geometric Conditions of Rigidity in Nongeneric settings, [Karpenkov2016]) (by F. Doray, J. Schepers, B. Servatius, and the author), for more details we refer to the mentioned articles.
Keywords
  Multidimensional continued fractions, Polyhedral surfaces, Integer geometry

1. Notation and Definitions

1.1. Tensegrities.

 

The subject of tensegrities was first considered by J.C. Maxwell in [Maxwell1864], who started to investigate first questions regarding force-loads for frameworks. Nowadays tensegrities are one of the leading directions of study in modern theory of rigidity (see, e.g., [Connelly1993] for further information). Let us recall several standard definitions.

Definition 1.1.
Fix a positive integer $ d$. Let $ G=(V,E)$ be an arbitrary graph without loops and multiple edges. Let it have $ n$ vertices $ v_1,\ldots , v_n$.
  • A configuration is a finite collection $ P$ of $ n$ labeled points $ (p_1,p_2,\ldots,p_n)$, where each point $ p_i$ is in a fixed Euclidean space $ \r^d$.
  • The realization of $ G$ with straight edges, induced by mapping $ v_j$ to $ p_j$ is called a tensegrity framework and it is denoted as $ G(P)$. (Here we allow the realization to have self-intersections).
  • A stress $ w$ on a framework is an assignment of real scalars $ w_{i,j}$ (called tensions ) to its edges $ p_ip_j$.
  • A stress $ w$ is called a self-stress if at every vertex $ p_i$ we have \begin{eqnarray*} \sum\limits_{\{j|j\ne i\}} w_{i,j}(p_j-p_i)=0. \end{eqnarray*}
  • A pair $ (G(P),w)$ is a tensegrity if $ w$ is a self-stress for the framework $ G(P)$.
  • If $ w_{i,j} {< } 0$ then we call the edge $ p_ip_j$ a cable , if $ w_{i,j} {> } 0$ we call it a strut .

1.2. Configuration Space of Tensegrities and its Stratification.

 

Denote by $ B_d(G)=(\r^d)^n$ the configuration space of all tensegrity frameworks. Let $ W(n)$ denote the linear space with coordinates $ w_{i,j}$ where $ 1\le i,j\le n$. It is clear that $ \dim W(n)=n^2$.

Definition 1.2.
Consider a framework $ G(P)\in B_d(G)$ and denote by $ W(G,P)$ the linear subspace of $ W(n)$ of all possible self-stresses for $ G(P)$. The space $ W(G,P)$ is the fiber at $ P$.
Definition 1.3.
Fibers $ W(G,P_1)$ and $ W(G,P_2)$ are said to be equivalent if there exists a homeomorphism $ \xi:W(G,P_1)\to W(G,P_2)$, such that for any $ w\in W(G,P_1)$ we have \begin{eqnarray*} \sgn\big(\xi(w_{i,j})\big)=\sgn\big(w_{i,j}\big) \end{eqnarray*} for every coordinate $ w_{i,j}$ of $ w$. Here $ \sgn$ denotes the standard sign function.

The described equivalence relation gives us a stratification of $ B_d(G)=(\r^d)^n.$ A stratum is by definition a maximal connected component of $ B_d(G)$ with equivalent fibers. In [Doray et al.2010] we prove that all strata are semialgebraic sets.

Remark.
According to all known examples the majority of the strata of codimension $ k$ are intersections of the strata of codimension 1 see e.g. [Doray et al.2010], [Karpenkov et al.2013]. So the most important case to study is the codimension 1 case.
Remark.
A stratification of a subgraph is a substratification of the original graph (i.e., each stratum for a subgraph is the union of certain strata for the original graph). Hence the case of complete graphs $ K_n$ is universal. This is straightforward as each extra edge contributes at least as much to dimensions of the fibers of a stratum as to the dimensions of the fibers of adjacent strata (locally).
Example 1.4.
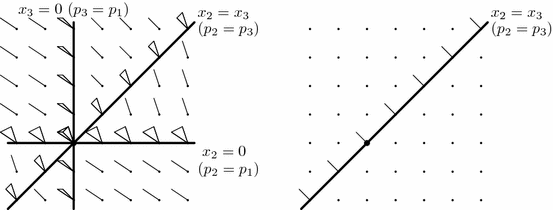
Let us consider a simple example of $ B_1(K_{3})$, namely we study tensegrities for a complete graph on three vertices and its realizations in the line. We assume that the line has a coordinate, so each point of $ B_1(K_3)$ is associated with three coordinates $ (x_1,x_2,x_3)$.

First we study a particular case $ x_1=0$, which we denote by $ B_1^0(K_3)$. The set $ B_1^0(K_3)$ has the following stratification (see Fig. 1, Left):

  • 1 stratum of codimension two: the origin. Here all three vertices coincide and the dimension of the fiber is 3.
  • 6 strata of codimension one: some pair of vertices coincide. The dimension of fiber is two.
  • 6 connected components of full dimension correspond to triple of distinct vertices. The dimension of a fiber is one.

It is clear that the dimension of the fiber for $ (x_1,x_2,x_3)$ coincides with the dimension of the fiber $ (0,x_2-x_1,x_3-x_1)$ for every $ x_1,x_2,x_3$. Therefore, we have \begin{eqnarray*} B_1(K_3)=B^0_1(K_3)\times \r^1. \end{eqnarray*}

Figure 1 Stratification of $ B^0_1(K_3)$ (left) and $ B^0_1(G_{1,2-3})$ (right).
Example 1.5.
Let now $ G_{1,2-3}$ be the graph on three vertices $ v_1,v_2,v_3$ with the only edge connecting $ v_2$ and $ v_3$. Then we have 1 stratum of codimension one defined by $ p_2=p_3$ (with fibers of dimension 1) and two connected components in the complement, i.e., where $ p_2\ne p_3$ (with fibers of dimension 0). As in previous example we have \begin{eqnarray*} B_1(G_{1,2-3})=B^0_1(G_{1,2-3})\times \r^1, \end{eqnarray*} where $ B^0_1(G_{1,2-3})$ is the stratification of the section $ x_1=0$ (see Fig. 1, Right).

2. Combinatoric Properties of Stratification

In Example 1.4 above we discussed a stratification of $ B_2(K_n)$. The most important information on the stratification contains its combinatorial structure, namely the list of strata of different dimensions and the adjacency diagram for the strata. For the combinatorial description of $ B_2(K_n)$ as in Example 1.4, for $ n=2,3,4,5$ we refer to [Karpenkov et al.2013]. There is not much known about more complicated configuration spaces. The next simplest and most interesting unstudied cases are listed in the following problem.

Problem 1.
Describe the combinatorics of $ B_2(K_6), B_3(K_4)$ and $ B_3(K_5)$.

As experiments show, for every codimension 1 stratum there exists a certain subgraph that locally identifies the stratum (i.e., for every point $ x$ of the stratum there exists a neighborhood $ B(x)$ such that every configuration in $ B(x)$ has a nonzero self-stress for the subgraph if and only if this point is on the stratum). This observation is valid for all dimensions $ d$.

Remark 2.1.
An illustration here are the cases $ B_1(K_3)$ and $ B_1(G_{1,2-3})$ of Examples 1.4 and 1.5. Here both codimension 1 strata of $ B_1(K_3)$ corresponding to $ p_2=p_3$ are in the union of the codimension 1 stratum of $ B_1(G_{1,2-3})$. This is a general situation. In particular for any graph $ G$ on $ n$ vertices the union of all strata for $ G$ is contained in the union of all strata for $ K_n$.

Let us say a few words about two-dimensional tensegrities. In the paper [Doray et al.2010] one can find the classification of all strata of codimension 1 for $ n\le 8$ points. For further examples, see the papers of [White and Whiteley1983], and [de Guzmán and Orden2004], [Guzmán and Orden2006]. In the paper [Karpenkov2017] it was shown how to approach every stratum for the case $ n=9$. The next case which contains unknown strata is $ n=10$ (see also Problem 8 below).

Problem 2.
Describe all the possible different types of strata for 10 points.
Problem 3.
Compute the number of different types of strata for $ n$ points with arbitrary $ n$.

In many cases the strata for different graphs coincide. So it is natural to ask the following question.

Problem 4.
Which subgraphs of $ K_n$ define the same stratifications?

Finally the following question remains open.

Problem 5.
Find all strata of codimension more than 1 that are not defined as an intersection of the closure of several codimension 1 strata.

Here we have only a trivial example of a graph on 2 vertices and one edge in the plane. It has one generic stratum of full dimension and one stratum of codimension 2, corresponding to two coinciding points.

3. Geometric Conditions Defining Strata in $ \r^2$

Majority of known examples in the planar case are expressed in terms of Cayley algebra. Recall that the objects of (planar) Cayley algebra are points and lines in the plane. Cayley algebra has two major operations:

  • join operation $ \vee$ is defined for a pair of points. The resulting object is the line joining these points.
  • meet operation $ \wedge$ is defined for a pair of lines. The meet of two lines is the intersection point of two lines.
For more information on Cayley algebras we refer to [Doubilet et al.1974], [White and McMillan1988], [Li2008], and [Karpenkov2017].

It turns out that many geometric conditions can be expressed in terms of Cayley operations. Let us illustrate this with the following example.

Example.
Let $ G=K_{3,3}$ be as in Fig. 2 (Left). A framework $ P=(p_1,\ldots, p_6)$ admits a non-zero tensegrity in $ \r^2$ if and only if six points $ p_1,p_2,\ldots,p_6$ are on a conic (see Fig. 2, Middle). This condition is described via Cayley algebra as Pascal's theorem: \begin{eqnarray*} q_1, q_2 \quad\text{and}\quad q_3\; \text{are in a line for} \quad \left\{\begin{array}{l} q_1=(p_1{\vee} p_2)\cap (p_4{\vee} p_5)\\ q_2=(p_2{\vee} p_3)\cap (p_5{\vee} p_6)\\ q_3=(p_3{\vee} p_4)\cap (p_6{\vee}p_1)\\ \end{array} \right., \end{eqnarray*} (Fig. 2, Right). Similar to Remark 2.1 the set of points of $ B(K_{3,3})$ that satisfy the above condition is the union of several strata for $ B(K_{3,3})$. The statement of this example is an exercise on surgeries on graphs introduced in [Doray et al.2010].
Figure 2 The graph $ K_{3,3}$ and the corresponding geometric conditions.

In fact in the above example, the property of 6 points to lie on one conic does not depend on the order of these points. Therefore, there are 60 different Cayley algebra systems defining the same stratum. This lead to the following important open problem.

Problem 6.
Which Cayley algebra systems define the same strata?

This problem is a kind of a question on finding generators and relations for the set of all conditions.

One of the main long-standing open problems on the Cayley strata description is as follows.

Problem 7.
Given a graph $ G$. Does there exist a Cayley algebra system (or several systems) describing the union of the codimension 1 tensegrity strata in the plane [i.e., the union of the codimension 1 strata of $ B_2(K_n)$]?

Recently this problem was solved in a weaker settings of extended Cayley algebra in [Karpenkov2017]. Nevertheless it is not clear if it is possible to avoid additional elements involved in the construction of [Karpenkov2017]. Here is an example of a graph for which the systems describing codimension 1 strata are not known.

Problem 8.
Write (if exist) Cayley algebra systems defining the strata for the following graph: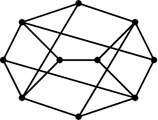

Currently this example is a strong candidate for a counterexample to Problem 7.

There is almost nothing known in multidimensional case.

Problem 9.
Develop theory of geometric conditions for strata in multidimensional case.

We refer to [White and Whiteley1983] for examples of geometric conditions in dimension 3.

References

[Connelly1993] Connelly, R.: Rigidity. In: Gruber, P.M., Wills, J.M. (eds.) Handbook of Convex Geometry, vol. A , pp. 223–271. North-Holland, Amsterdam (1993)
[de Guzmán and Orden2004] de Guzmán, M., Orden, D.: Finding tensegrity structures: Geometric and symbolic aproaches, In: Proceedings of EACA-2004, p 167–172 (2004)
[Guzmán and Orden2006] de Guzmán, M., Orden, D.: From graphs to tensegrity structures: geometric and symbolic approaches. Publ. Mat. 50 , 279–299 (2006)
[Doray et al.2010] Doray, F., Karpenkov, O., Schepers, J.: Geometry of configuration spaces of tensegrities. Discrete Comput. Geom. 43 (2), 436–466 (2010)
[Doubilet et al.1974] Doubilet, P., Rota, G.-C., Stein, J.: On the foundations of combinatorial theory. IX. Combinatorial methods in invariant theory, Studies. Appl. Math. 53 , 185–216 (1974)
[Karpenkov2017] Karpenkov, O.: The combinatorial geometry of stresses in frameworks, preprint (2017), arXiv:1512.02563 [math.MG]
[Karpenkov2016] Karpenkov, O.: Geometric conditions of rigidity in nongeneric settings. In: Sitharam, M., St. John, A., Sidman, J. (eds.) Handbook of Geometric Constraint Systems Principles, chapter 15 (2018) (accepted)
[Karpenkov et al.2013] Karpenkov, O., Schepers, J., Servatius, B.: On stratifications for planar tensegrities with a small number of vertices. ARS Math Contemp 6 (2), 305–322 (2013)
[Li2008] Li, H.: Invariant algebras and geometric reasoning. With a foreword by David Hestenes. World Scientific Publishing, Hackensack (2008)
[Maxwell1864] Maxwell, J.C.: On reciprocal figures and diagrams of forces. Philos. Mag. 4 (27), 250–261 (1864)
[White and McMillan1988] White, N.L., McMillan, T.: Cayley factorization. Symbolic and algebraic computation, Rome, pp. 521–533. Springer, Berlin (1988). (Lecture Notes in Comput. Sci., 358 1989)
[White and Whiteley1983] White, N.L., Whiteley, W.: The algebraic geometry of stresses in frameworks. SIAM J. Alg. Disc. Meth. 4 (4), 481–511 (1983)